Sublinear Variational Optimization of Gaussian Mixture Models with Millions to Billions of Parameters

Gaussian Mixture Models (GMMs) range among the most frequently used machine learning models. However, training large, general GMMs becomes computationally prohibitive for datasets with many data points $N$ of high-dimensionality $D$. For GMMs with arbitrary covariances, we here derive a highly efficient variational approximation, which is integrated with mixtures of factor analyzers (MFAs). For GMMs with $C$ components, our proposed algorithm significantly reduces runtime complexity per iteration from $\mathcal{O}(NCD^2)$ to a complexity scaling linearly with $D$ and remaining constant w.r.t. $C$. Numerical validation of this theoretical complexity reduction then shows the following: the distance evaluations required for the entire GMM optimization process scale sublinearly with $NC$. On large-scale benchmarks, this sublinearity results in speed-ups of an order-of-magnitude compared to the state-of-the-art. As a proof of concept, we train GMMs with over 10 billion parameters on about 100 million images, and observe training times of approximately nine hours on a single state-of-the-art CPU.

Maximal Causes for Exponential Family Observables

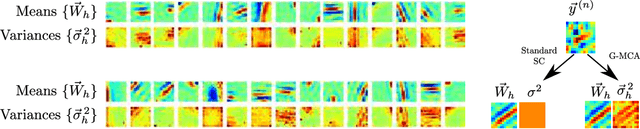
The data model of standard sparse coding assumes a weighted linear summation of latents to determine the mean of Gaussian observation noise. However, such a linear summation of latents is often at odds with non-Gaussian observables (e.g., means of the Bernoulli distribution have to lie in the unit interval), and also in the Gaussian case it can be difficult to justify for many types of data. Alternative superposition models (i.e., links between latents and observables) have therefore been investigated repeatedly. Here we show that using the maximum instead of a linear sum to link latents to observables allows for the derivation of very general and concise parameter update equations. Concretely, we derive a set of update equations that has the same functional form for all distributions of the exponential family (given that derivatives w.r.t. their parameters can be taken). Our results consequently allow for the development of latent variable models for commonly as well as for unusually distributed data. We numerically verify our analytical result assuming standard Gaussian, Gamma, Poisson, Bernoulli and Exponential distributions and point to some potential applications.

Accelerated Training of Large-Scale Gaussian Mixtures by a Merger of Sublinear Approaches

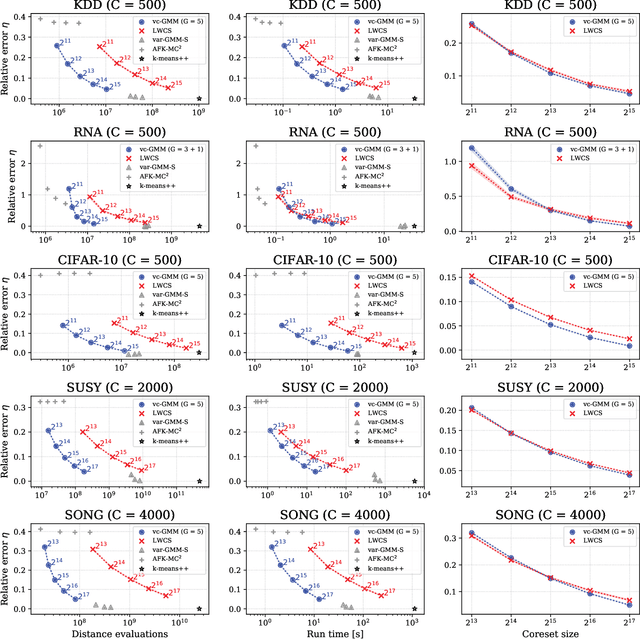
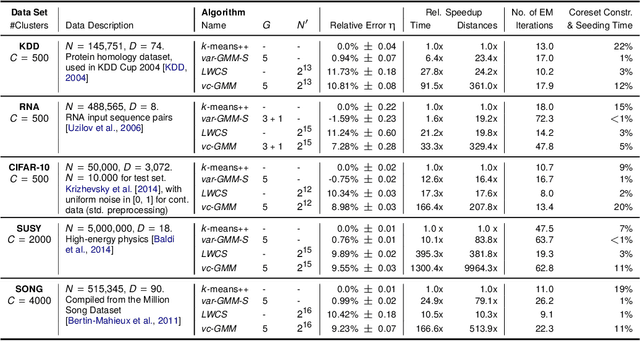
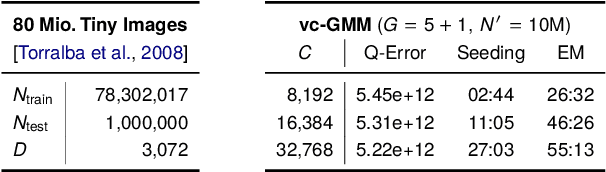
We combine two recent lines of research on sublinear clustering to significantly increase the efficiency of training Gaussian mixture models (GMMs) on large scale problems. First, we use a novel truncated variational EM approach for GMMs with isotropic Gaussians in order to increase clustering efficiency for large $C$ (many clusters). Second, we use recent coreset approaches to increase clustering efficiency for large $N$ (many data points). In order to derive a novel accelerated algorithm, we first show analytically how variational EM and coreset objectives can be merged to give rise to a new, combined clustering objective. Each iteration of the novel algorithm derived from this merged objective is then shown to have a run-time cost of $\mathcal{O}(N' G^2 D)$ per iteration, where $N'<N$ is the coreset size and $G^2<C$ is a constant related to the extent of local cluster neighborhoods. While enabling clustering with a strongly reduced number of distance evaluations per iteration, the combined approach is observed to still very effectively increase the clustering objective. In a series of numerical experiments on standard benchmarks, we use efficient seeding for initialization and evaluate the net computational demand of the merged approach in comparison to (already highly efficient) recent approaches. As result, depending on the dataset and number of clusters, the merged algorithm shows several times (and up to an order of magnitude) faster execution times to reach the same quantization errors as algorithms based on coresets or on variational EM alone.