Sublinear Variational Optimization of Gaussian Mixture Models with Millions to Billions of Parameters

Gaussian Mixture Models (GMMs) range among the most frequently used machine learning models. However, training large, general GMMs becomes computationally prohibitive for datasets with many data points $N$ of high-dimensionality $D$. For GMMs with arbitrary covariances, we here derive a highly efficient variational approximation, which is integrated with mixtures of factor analyzers (MFAs). For GMMs with $C$ components, our proposed algorithm significantly reduces runtime complexity per iteration from $\mathcal{O}(NCD^2)$ to a complexity scaling linearly with $D$ and remaining constant w.r.t. $C$. Numerical validation of this theoretical complexity reduction then shows the following: the distance evaluations required for the entire GMM optimization process scale sublinearly with $NC$. On large-scale benchmarks, this sublinearity results in speed-ups of an order-of-magnitude compared to the state-of-the-art. As a proof of concept, we train GMMs with over 10 billion parameters on about 100 million images, and observe training times of approximately nine hours on a single state-of-the-art CPU.

The Evidence Lower Bound of Variational Autoencoders Converges to a Sum of Three Entropies

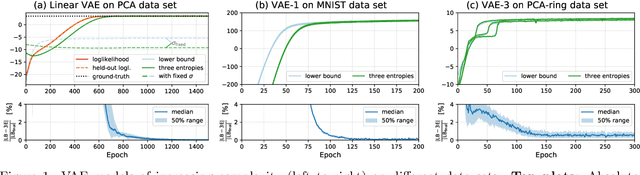
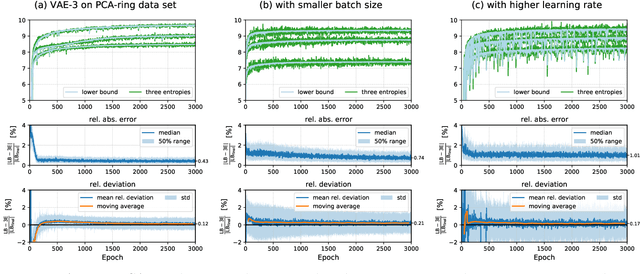
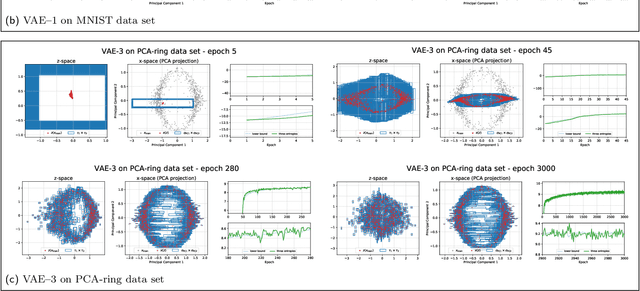
The central objective function of a variational autoencoder (VAE) is its variational lower bound. Here we show that for standard VAEs the variational bound is at convergence equal to the sum of three entropies: the (negative) entropy of the latent distribution, the expected (negative) entropy of the observable distribution, and the average entropy of the variational distributions. Our derived analytical results are exact and apply for small as well as complex neural networks for decoder and encoder. Furthermore, they apply for finite and infinitely many data points and at any stationary point (including local and global maxima). As a consequence, we show that the variance parameters of encoder and decoder play the key role in determining the values of variational bounds at convergence. Furthermore, the obtained results can allow for closed-form analytical expressions at convergence, which may be unexpected as neither variational bounds of VAEs nor log-likelihoods of VAEs are closed-form during learning. As our main contribution, we provide the proofs for convergence of standard VAEs to sums of entropies. Furthermore, we numerically verify our analytical results and discuss some potential applications. The obtained equality to entropy sums provides novel information on those points in parameter space that variational learning converges to. As such, we believe they can potentially significantly contribute to our understanding of established as well as novel VAE approaches.

Accelerated Training of Large-Scale Gaussian Mixtures by a Merger of Sublinear Approaches

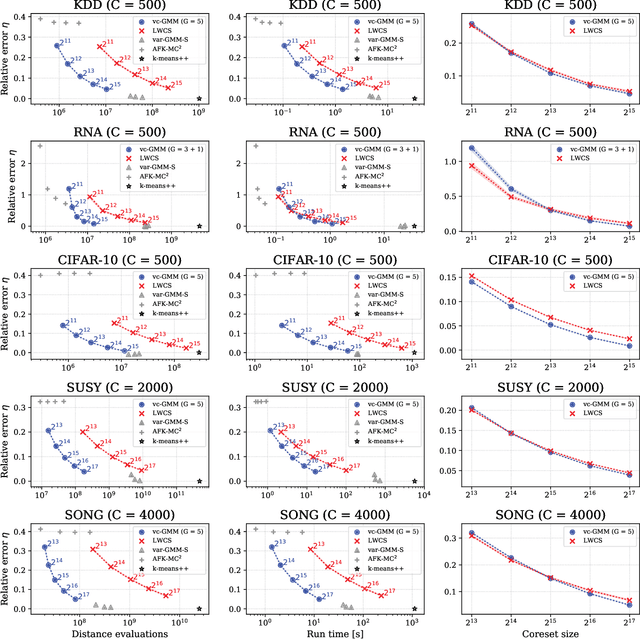
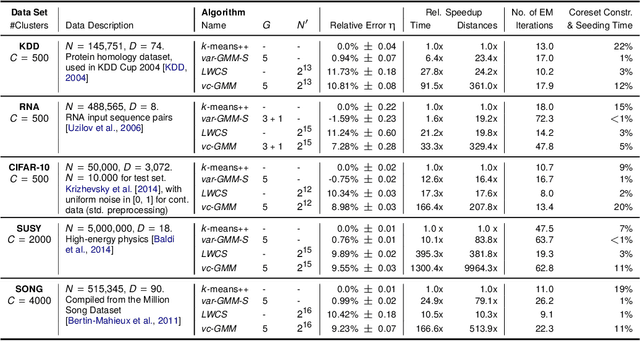
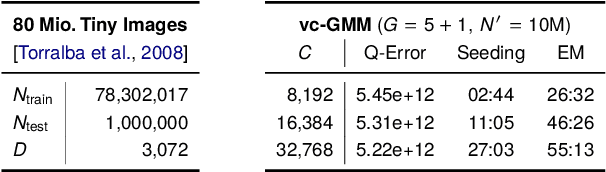
We combine two recent lines of research on sublinear clustering to significantly increase the efficiency of training Gaussian mixture models (GMMs) on large scale problems. First, we use a novel truncated variational EM approach for GMMs with isotropic Gaussians in order to increase clustering efficiency for large $C$ (many clusters). Second, we use recent coreset approaches to increase clustering efficiency for large $N$ (many data points). In order to derive a novel accelerated algorithm, we first show analytically how variational EM and coreset objectives can be merged to give rise to a new, combined clustering objective. Each iteration of the novel algorithm derived from this merged objective is then shown to have a run-time cost of $\mathcal{O}(N' G^2 D)$ per iteration, where $N'<N$ is the coreset size and $G^2<C$ is a constant related to the extent of local cluster neighborhoods. While enabling clustering with a strongly reduced number of distance evaluations per iteration, the combined approach is observed to still very effectively increase the clustering objective. In a series of numerical experiments on standard benchmarks, we use efficient seeding for initialization and evaluate the net computational demand of the merged approach in comparison to (already highly efficient) recent approaches. As result, depending on the dataset and number of clusters, the merged algorithm shows several times (and up to an order of magnitude) faster execution times to reach the same quantization errors as algorithms based on coresets or on variational EM alone.

Can clustering scale sublinearly with its clusters? A variational EM acceleration of GMMs and $k$-means

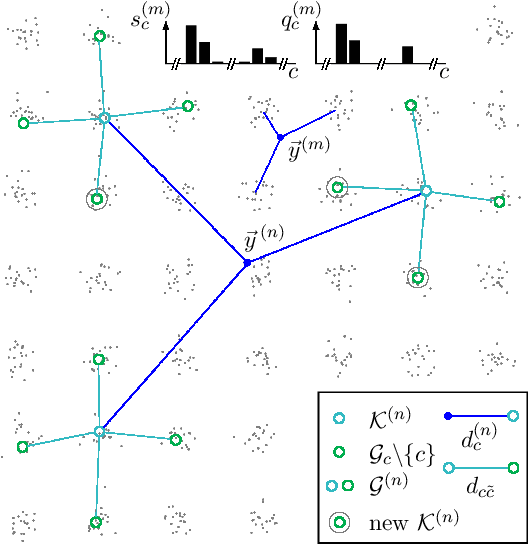
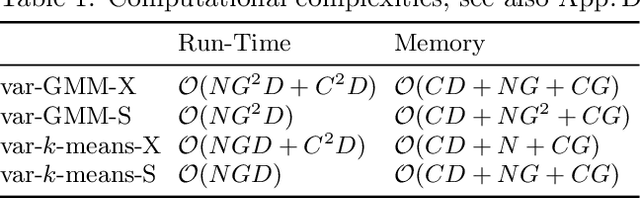
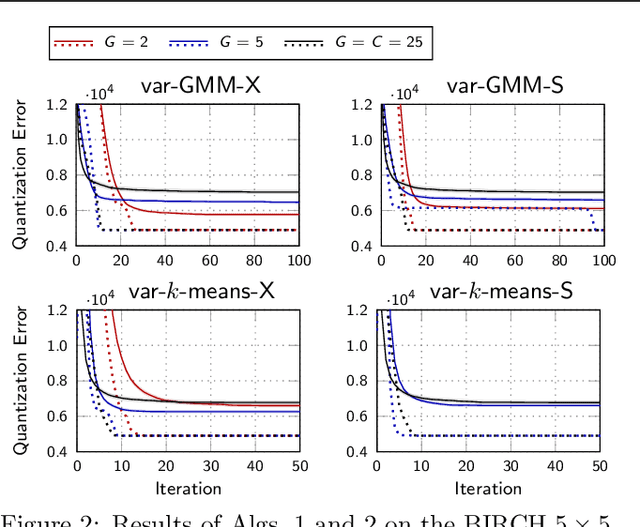
One iteration of standard $k$-means (i.e., Lloyd's algorithm) or standard EM for Gaussian mixture models (GMMs) scales linearly with the number of clusters $C$, data points $N$, and data dimensionality $D$. In this study, we explore whether one iteration of $k$-means or EM for GMMs can scale sublinearly with $C$ at run-time, while improving the clustering objective remains effective. The tool we apply for complexity reduction is variational EM, which is typically used to make training of generative models with exponentially many hidden states tractable. Here, we apply novel theoretical results on truncated variational EM to make tractable clustering algorithms more efficient. The basic idea is to use a partial variational E-step which reduces the linear complexity of $\mathcal{O}(NCD)$ required for a full E-step to a sublinear complexity. Our main observation is that the linear dependency on $C$ can be reduced to a dependency on a much smaller parameter $G$ which relates to cluster neighborhood relations. We focus on two versions of partial variational EM for clustering: variational GMM, scaling with $\mathcal{O}(NG^2D)$, and variational $k$-means, scaling with $\mathcal{O}(NGD)$ per iteration. Empirical results show that these algorithms still require comparable numbers of iterations to improve the clustering objective to same values as $k$-means. For data with many clusters, we consequently observe reductions of net computational demands between two and three orders of magnitude. More generally, our results provide substantial empirical evidence in favor of clustering to scale sublinearly with $C$.

Truncated Variational EM for Semi-Supervised Neural Simpletrons

Inference and learning for probabilistic generative networks is often very challenging and typically prevents scalability to as large networks as used for deep discriminative approaches. To obtain efficiently trainable, large-scale and well performing generative networks for semi-supervised learning, we here combine two recent developments: a neural network reformulation of hierarchical Poisson mixtures (Neural Simpletrons), and a novel truncated variational EM approach (TV-EM). TV-EM provides theoretical guarantees for learning in generative networks, and its application to Neural Simpletrons results in particularly compact, yet approximately optimal, modifications of learning equations. If applied to standard benchmarks, we empirically find, that learning converges in fewer EM iterations, that the complexity per EM iteration is reduced, and that final likelihood values are higher on average. For the task of classification on data sets with few labels, learning improvements result in consistently lower error rates if compared to applications without truncation. Experiments on the MNIST data set herein allow for comparison to standard and state-of-the-art models in the semi-supervised setting. Further experiments on the NIST SD19 data set show the scalability of the approach when a manifold of additional unlabeled data is available.

Neural Simpletrons - Minimalistic Directed Generative Networks for Learning with Few Labels

Classifiers for the semi-supervised setting often combine strong supervised models with additional learning objectives to make use of unlabeled data. This results in powerful though very complex models that are hard to train and that demand additional labels for optimal parameter tuning, which are often not given when labeled data is very sparse. We here study a minimalistic multi-layer generative neural network for semi-supervised learning in a form and setting as similar to standard discriminative networks as possible. Based on normalized Poisson mixtures, we derive compact and local learning and neural activation rules. Learning and inference in the network can be scaled using standard deep learning tools for parallelized GPU implementation. With the single objective of likelihood optimization, both labeled and unlabeled data are naturally incorporated into learning. Empirical evaluations on standard benchmarks show, that for datasets with few labels the derived minimalistic network improves on all classical deep learning approaches and is competitive with their recent variants without the need of additional labels for parameter tuning. Furthermore, we find that the studied network is the best performing monolithic (`non-hybrid') system for few labels, and that it can be applied in the limit of very few labels, where no other system has been reported to operate so far.