Can clustering scale sublinearly with its clusters? A variational EM acceleration of GMMs and $k$-means
Paper and Code
Apr 17, 2018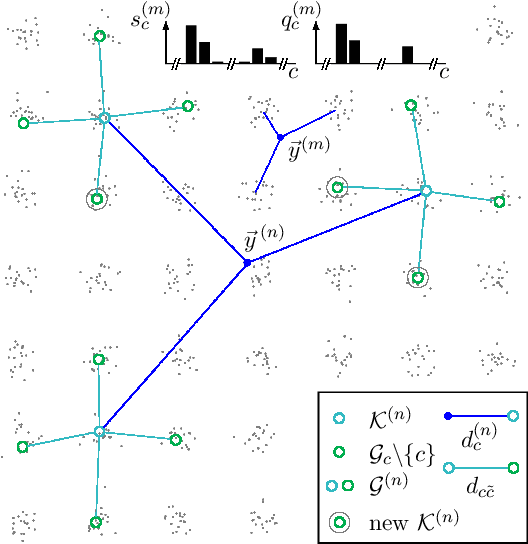
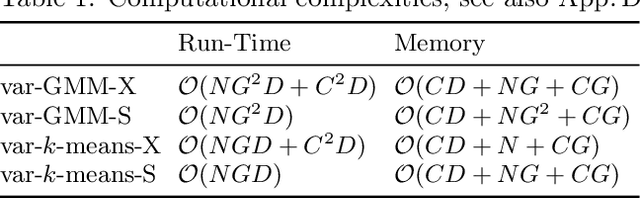
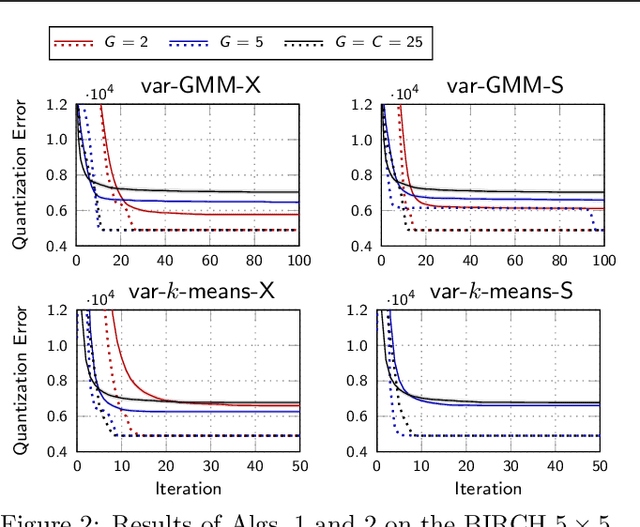

One iteration of standard $k$-means (i.e., Lloyd's algorithm) or standard EM for Gaussian mixture models (GMMs) scales linearly with the number of clusters $C$, data points $N$, and data dimensionality $D$. In this study, we explore whether one iteration of $k$-means or EM for GMMs can scale sublinearly with $C$ at run-time, while improving the clustering objective remains effective. The tool we apply for complexity reduction is variational EM, which is typically used to make training of generative models with exponentially many hidden states tractable. Here, we apply novel theoretical results on truncated variational EM to make tractable clustering algorithms more efficient. The basic idea is to use a partial variational E-step which reduces the linear complexity of $\mathcal{O}(NCD)$ required for a full E-step to a sublinear complexity. Our main observation is that the linear dependency on $C$ can be reduced to a dependency on a much smaller parameter $G$ which relates to cluster neighborhood relations. We focus on two versions of partial variational EM for clustering: variational GMM, scaling with $\mathcal{O}(NG^2D)$, and variational $k$-means, scaling with $\mathcal{O}(NGD)$ per iteration. Empirical results show that these algorithms still require comparable numbers of iterations to improve the clustering objective to same values as $k$-means. For data with many clusters, we consequently observe reductions of net computational demands between two and three orders of magnitude. More generally, our results provide substantial empirical evidence in favor of clustering to scale sublinearly with $C$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge