Black-box density function estimation using recursive partitioning
Paper and Code
Oct 26, 2020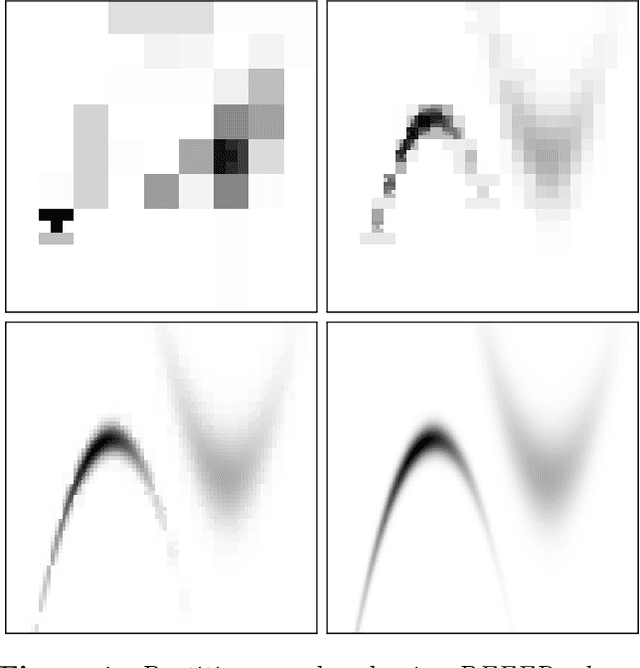
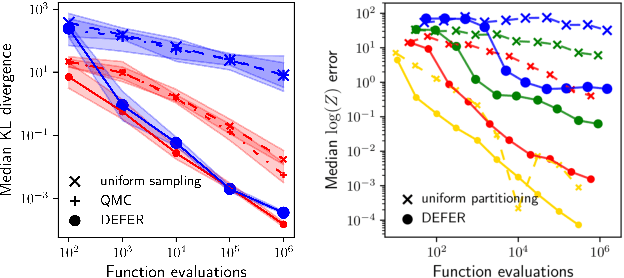
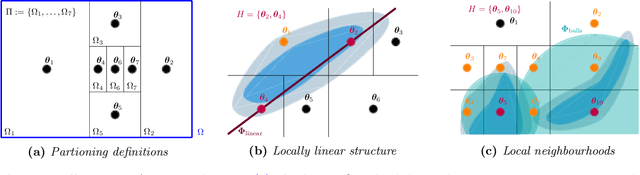

We present a novel approach to Bayesian inference and general Bayesian computation that is defined through a recursive partitioning of the sample space. It does not rely on gradients, nor require any problem-specific tuning, and is asymptotically exact for any density function with a bounded domain. The output is an approximation to the whole density function including the normalization constant, via partitions organized in efficient data structures. This allows for evidence estimation, as well as approximate posteriors that allow for fast sampling and fast evaluations of the density. It shows competitive performance to recent state-of-the-art methods on synthetic and real-world problem examples including parameter inference for gravitational-wave physics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge