Spatio-temporal Gaussian processes modeling of dynamical systems in systems biology
Paper and Code
Oct 17, 2016
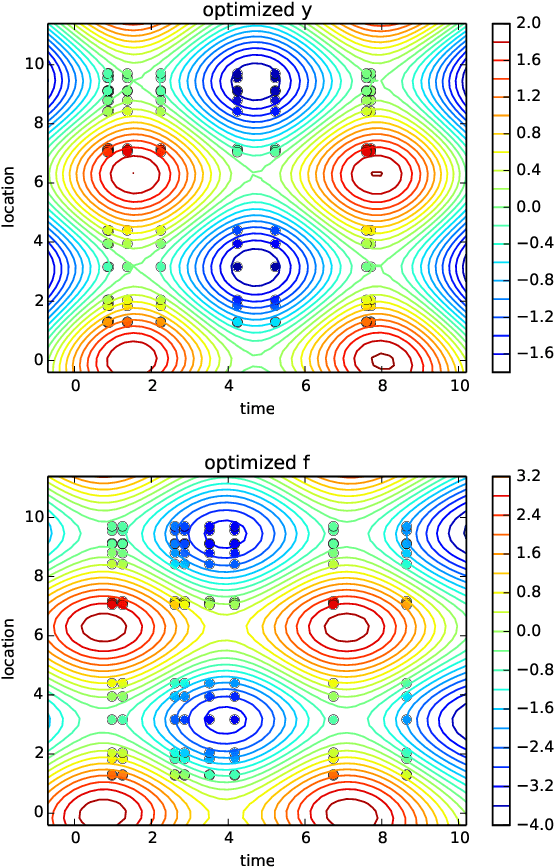
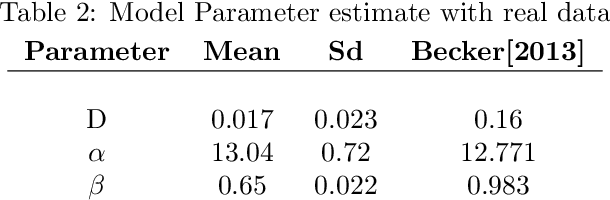
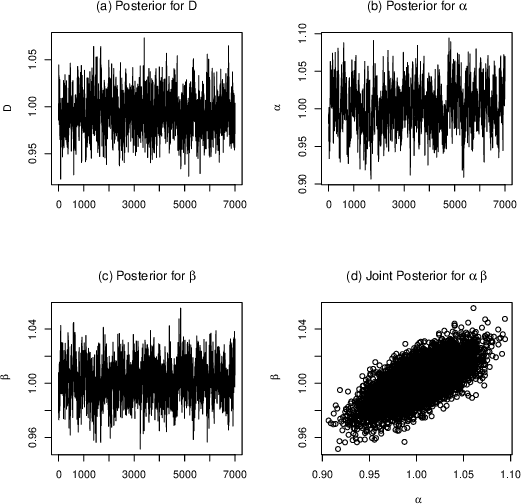
Quantitative modeling of post-transcriptional regulation process is a challenging problem in systems biology. A mechanical model of the regulatory process needs to be able to describe the available spatio-temporal protein concentration and mRNA expression data and recover the continuous spatio-temporal fields. Rigorous methods are required to identify model parameters. A promising approach to deal with these difficulties is proposed using Gaussian process as a prior distribution over the latent function of protein concentration and mRNA expression. In this study, we consider a partial differential equation mechanical model with differential operators and latent function. Since the operators at stake are linear, the information from the physical model can be encoded into the kernel function. Hybrid Monte Carlo methods are employed to carry out Bayesian inference of the partial differential equation parameters and Gaussian process kernel parameters. The spatio-temporal field of protein concentration and mRNA expression are reconstructed without explicitly solving the partial differential equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge