Heat kernel and intrinsic Gaussian processes on manifolds

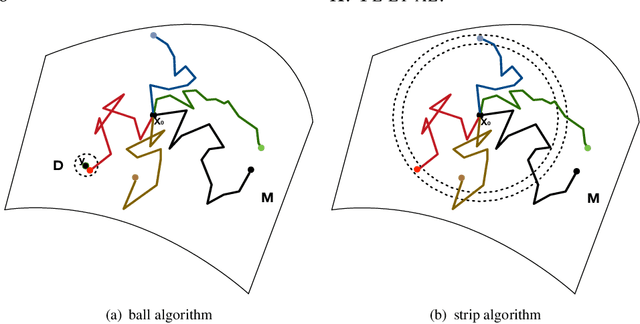
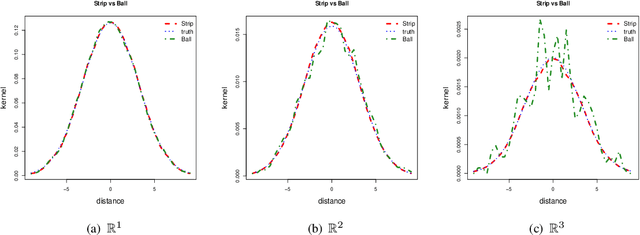
There is an increasing interest in the problem of nonparametric regression like Gaussian processes with predictors locating on manifold. Some recent researches developed intrinsic Gaussian processes by using the transition density of the Brownian motion on submanifolds of $\mathbb R^2$ and $\mathbb R^3$ to approximate the heat kernels. {However}, when the dimension of a manifold is bigger than two, the existing method struggled to get good estimation of the heat kernel. In this work, we propose an intrinsic approach of constructing the Gaussian process on \if more \fi general manifolds \if {\color{red} in the matrix Lie groups} \fi such as orthogonal groups, unitary groups, Stiefel manifolds and Grassmannian manifolds. The heat kernel is estimated by simulating Brownian motion sample paths via the exponential map, which does not depend on the embedding of the manifold. To be more precise, this intrinsic method has the following features: (i) it is effective for high dimensional manifolds; (ii) it is applicable to arbitrary manifolds; (iii) it does not require the global parametrisation or embedding which may introduce redundant parameters; (iv) results obtained by this method do not depend on the ambient space of the manifold. Based on this method, we propose the ball algorithm for arbitrary manifolds and the strip algorithm for manifolds with extra symmetries, which is both theoretically proven and numerically tested to be much more efficient than the ball algorithm. A regression example on the projective space of dimension eight is given in this work, which demonstrates that our intrinsic method for Gaussian process is practically effective in great generality.