Random Forests Weighted Local Fréchet Regression with Theoretical Guarantee
Paper and Code
Feb 10, 2022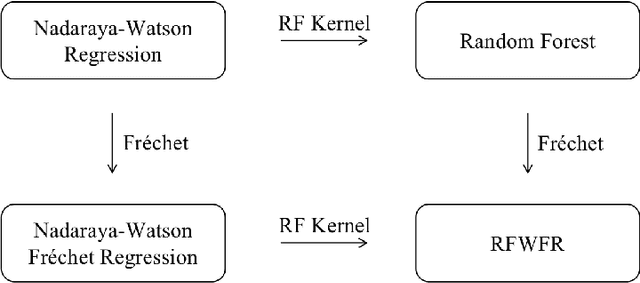
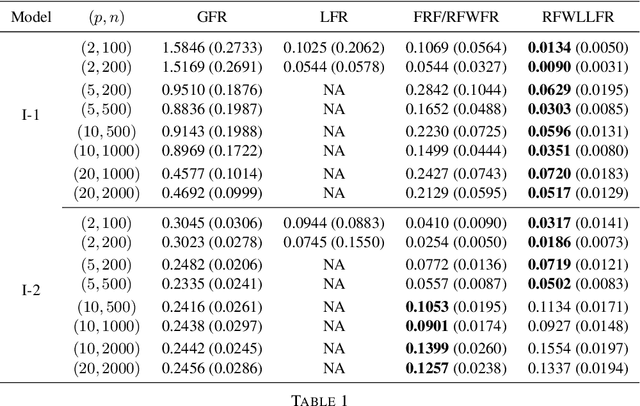
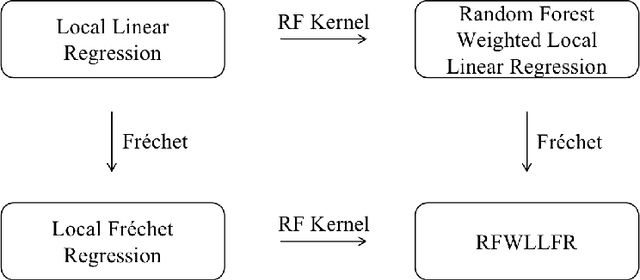

Statistical analysis is increasingly confronted with complex data from general metric spaces, such as symmetric positive definite matrix-valued data and probability distribution functions. [47] and [17] establish a general paradigm of Fr\'echet regression with complex metric space valued responses and Euclidean predictors. However, their proposed local Fr\'echet regression approach involves nonparametric kernel smoothing and suffers from the curse of dimensionality. To address this issue, we in this paper propose a novel random forests weighted local Fr\'echet regression paradigm. The main mechanism of our approach relies on the adaptive kernels generated by random forests. Our first method utilizes these weights as the local average to solve the Fr\'echet mean, while the second method performs local linear Fr\'echet regression, making both methods locally adaptive. Our proposals significantly improve existing Fr\'echet regression methods. Based on the theory of infinite order U-processes and infinite order Mmn-estimator, we establish the consistency, rate of convergence, and asymptotic normality for our proposed random forests weighted Fr\'echet regression estimator, which covers the current large sample theory of random forests with Euclidean responses as a special case. Numerical studies show the superiority of our proposed two methods for Fr\'echet regression with several commonly encountered types of responses such as probability distribution functions, symmetric positive definite matrices, and sphere data. The practical merits of our proposals are also demonstrated through the application to the human mortality distribution data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge