CausalEGM: a general causal inference framework by encoding generative modeling

Although understanding and characterizing causal effects have become essential in observational studies, it is challenging when the confounders are high-dimensional. In this article, we develop a general framework $\textit{CausalEGM}$ for estimating causal effects by encoding generative modeling, which can be applied in both binary and continuous treatment settings. Under the potential outcome framework with unconfoundedness, we establish a bidirectional transformation between the high-dimensional confounders space and a low-dimensional latent space where the density is known (e.g., multivariate normal distribution). Through this, CausalEGM simultaneously decouples the dependencies of confounders on both treatment and outcome and maps the confounders to the low-dimensional latent space. By conditioning on the low-dimensional latent features, CausalEGM can estimate the causal effect for each individual or the average causal effect within a population. Our theoretical analysis shows that the excess risk for CausalEGM can be bounded through empirical process theory. Under an assumption on encoder-decoder networks, the consistency of the estimate can be guaranteed. In a series of experiments, CausalEGM demonstrates superior performance over existing methods for both binary and continuous treatments. Specifically, we find CausalEGM to be substantially more powerful than competing methods in the presence of large sample sizes and high dimensional confounders. The software of CausalEGM is freely available at https://github.com/SUwonglab/CausalEGM.

Subgraph Frequency Distribution Estimation using Graph Neural Networks

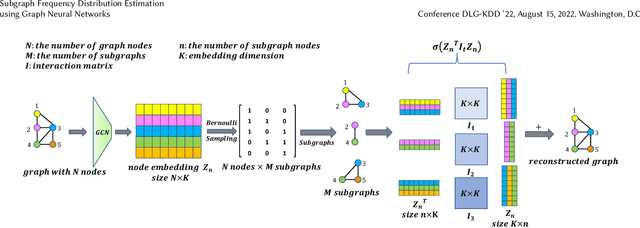
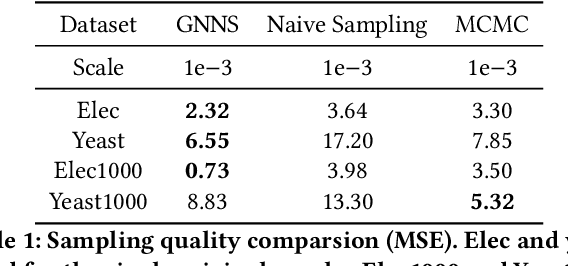
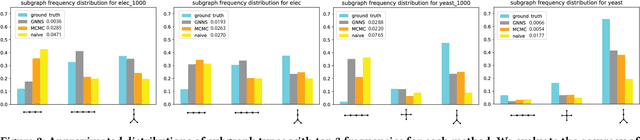
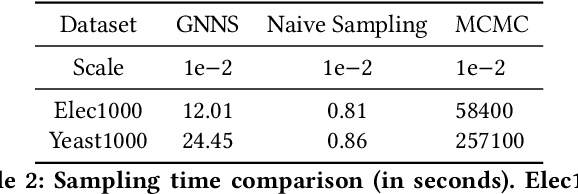
Small subgraphs (graphlets) are important features to describe fundamental units of a large network. The calculation of the subgraph frequency distributions has a wide application in multiple domains including biology and engineering. Unfortunately due to the inherent complexity of this task, most of the existing methods are computationally intensive and inefficient. In this work, we propose GNNS, a novel representational learning framework that utilizes graph neural networks to sample subgraphs efficiently for estimating their frequency distribution. Our framework includes an inference model and a generative model that learns hierarchical embeddings of nodes, subgraphs, and graph types. With the learned model and embeddings, subgraphs are sampled in a highly scalable and parallel way and the frequency distribution estimation is then performed based on these sampled subgraphs. Eventually, our methods achieve comparable accuracy and a significant speedup by three orders of magnitude compared to existing methods.