A Mean-Field Analysis of Neural Gradient Descent-Ascent: Applications to Functional Conditional Moment Equations

We study minimax optimization problems defined over infinite-dimensional function classes. In particular, we restrict the functions to the class of overparameterized two-layer neural networks and study (i) the convergence of the gradient descent-ascent algorithm and (ii) the representation learning of the neural network. As an initial step, we consider the minimax optimization problem stemming from estimating a functional equation defined by conditional expectations via adversarial estimation, where the objective function is quadratic in the functional space. For this problem, we establish convergence under the mean-field regime by considering the continuous-time and infinite-width limit of the optimization dynamics. Under this regime, gradient descent-ascent corresponds to a Wasserstein gradient flow over the space of probability measures defined over the space of neural network parameters. We prove that the Wasserstein gradient flow converges globally to a stationary point of the minimax objective at a $\mathcal{O}(T^{-1} + \alpha^{-1} ) $ sublinear rate, and additionally finds the solution to the functional equation when the regularizer of the minimax objective is strongly convex. Here $T$ denotes the time and $\alpha$ is a scaling parameter of the neural network. In terms of representation learning, our results show that the feature representation induced by the neural networks is allowed to deviate from the initial one by the magnitude of $\mathcal{O}(\alpha^{-1})$, measured in terms of the Wasserstein distance. Finally, we apply our general results to concrete examples including policy evaluation, nonparametric instrumental variable regression, and asset pricing.

Synchronized Dual-arm Rearrangement via Cooperative mTSP

Synchronized dual-arm rearrangement is widely studied as a common scenario in industrial applications. It often faces scalability challenges due to the computational complexity of robotic arm rearrangement and the high-dimensional nature of dual-arm planning. To address these challenges, we formulated the problem as cooperative mTSP, a variant of mTSP where agents share cooperative costs, and utilized reinforcement learning for its solution. Our approach involved representing rearrangement tasks using a task state graph that captured spatial relationships and a cooperative cost matrix that provided details about action costs. Taking these representations as observations, we designed an attention-based network to effectively combine them and provide rational task scheduling. Furthermore, a cost predictor is also introduced to directly evaluate actions during both training and planning, significantly expediting the planning process. Our experimental results demonstrate that our approach outperforms existing methods in terms of both performance and planning efficiency.

SGMM: Stochastic Approximation to Generalized Method of Moments

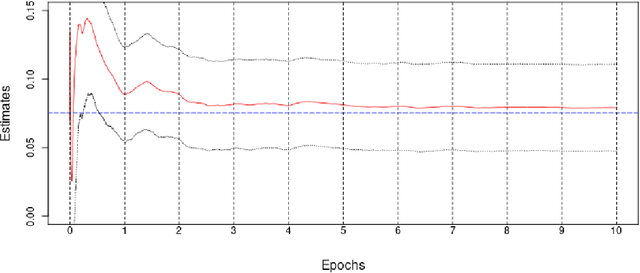
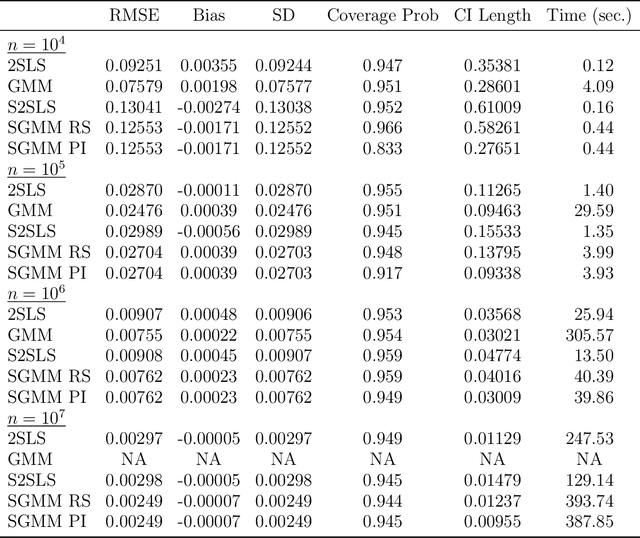
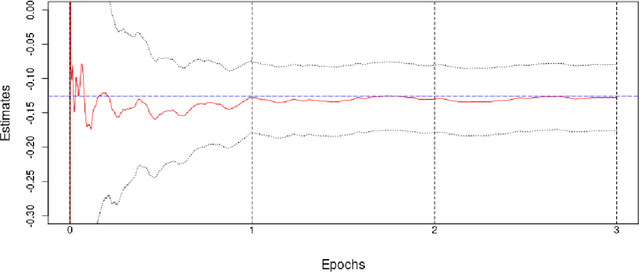
We introduce a new class of algorithms, Stochastic Generalized Method of Moments (SGMM), for estimation and inference on (overidentified) moment restriction models. Our SGMM is a novel stochastic approximation alternative to the popular Hansen (1982) (offline) GMM, and offers fast and scalable implementation with the ability to handle streaming datasets in real time. We establish the almost sure convergence, and the (functional) central limit theorem for the inefficient online 2SLS and the efficient SGMM. Moreover, we propose online versions of the Durbin-Wu-Hausman and Sargan-Hansen tests that can be seamlessly integrated within the SGMM framework. Extensive Monte Carlo simulations show that as the sample size increases, the SGMM matches the standard (offline) GMM in terms of estimation accuracy and gains over computational efficiency, indicating its practical value for both large-scale and online datasets. We demonstrate the efficacy of our approach by a proof of concept using two well known empirical examples with large sample sizes.

STEEL: Singularity-aware Reinforcement Learning

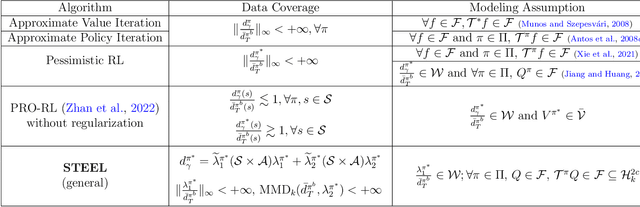
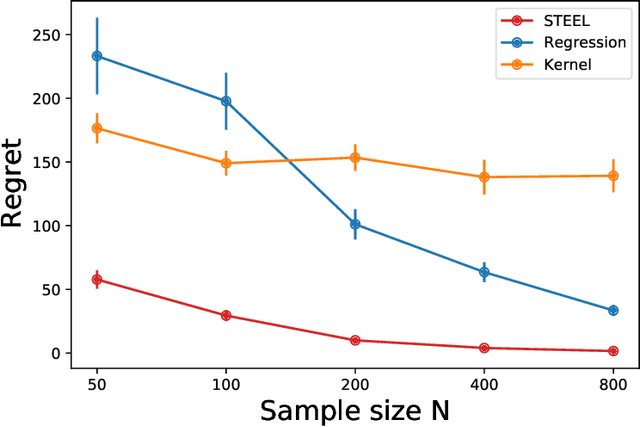
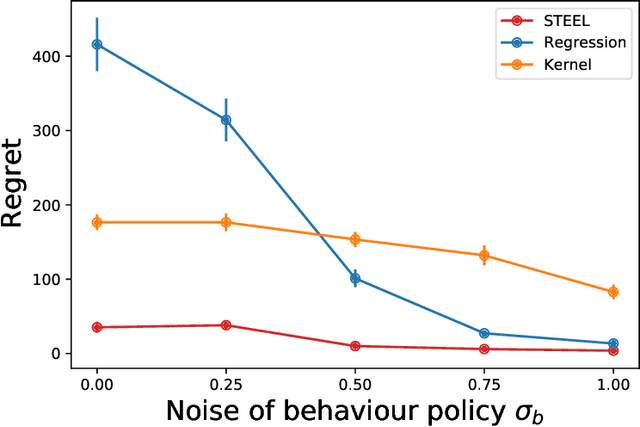
Batch reinforcement learning (RL) aims at finding an optimal policy in a dynamic environment in order to maximize the expected total rewards by leveraging pre-collected data. A fundamental challenge behind this task is the distributional mismatch between the batch data generating process and the distribution induced by target policies. Nearly all existing algorithms rely on the absolutely continuous assumption on the distribution induced by target policies with respect to the data distribution so that the batch data can be used to calibrate target policies via the change of measure. However, the absolute continuity assumption could be violated in practice, especially when the state-action space is large or continuous. In this paper, we propose a new batch RL algorithm without requiring absolute continuity in the setting of an infinite-horizon Markov decision process with continuous states and actions. We call our algorithm STEEL: SingulariTy-awarE rEinforcement Learning. Our algorithm is motivated by a new error analysis on off-policy evaluation, where we use maximum mean discrepancy, together with distributionally robust optimization, to characterize the error of off-policy evaluation caused by the possible singularity and to enable the power of model extrapolation. By leveraging the idea of pessimism and under some mild conditions, we derive a finite-sample regret guarantee for our proposed algorithm without imposing absolute continuity. Compared with existing algorithms, STEEL only requires some minimal data-coverage assumption and thus greatly enhances the applicability and robustness of batch RL. Extensive simulation studies and one real experiment on personalized pricing demonstrate the superior performance of our method when facing possible singularity in batch RL.

Inference on Time Series Nonparametric Conditional Moment Restrictions Using General Sieves

General nonlinear sieve learnings are classes of nonlinear sieves that can approximate nonlinear functions of high dimensional variables much more flexibly than various linear sieves (or series). This paper considers general nonlinear sieve quasi-likelihood ratio (GN-QLR) based inference on expectation functionals of time series data, where the functionals of interest are based on some nonparametric function that satisfy conditional moment restrictions and are learned using multilayer neural networks. While the asymptotic normality of the estimated functionals depends on some unknown Riesz representer of the functional space, we show that the optimally weighted GN-QLR statistic is asymptotically Chi-square distributed, regardless whether the expectation functional is regular (root-$n$ estimable) or not. This holds when the data are weakly dependent beta-mixing condition. We apply our method to the off-policy evaluation in reinforcement learning, by formulating the Bellman equation into the conditional moment restriction framework, so that we can make inference about the state-specific value functional using the proposed GN-QLR method with time series data. In addition, estimating the averaged partial means and averaged partial derivatives of nonparametric instrumental variables and quantile IV models are also presented as leading examples. Finally, a Monte Carlo study shows the finite sample performance of the procedure

Adaptive incomplete multi-view learning via tensor graph completion

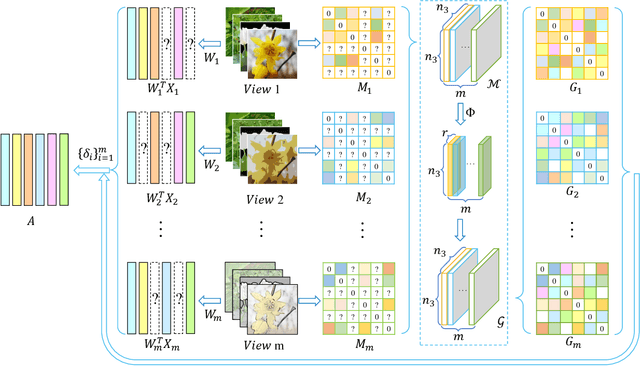
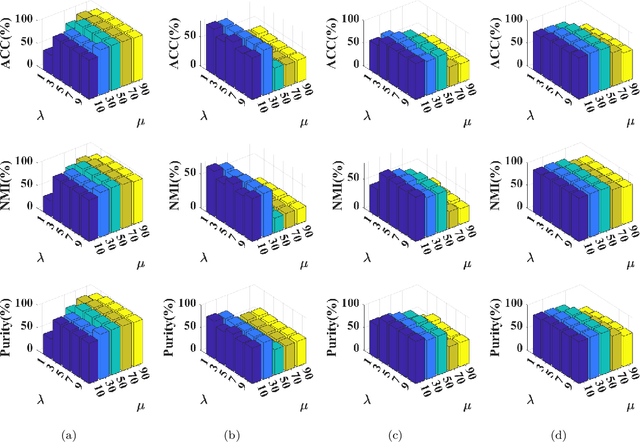
With the advancement of the data acquisition techniques, multi-view learning has become a hot topic. Some multi-view learning methods assume that the multi-view data is complete, which means that all instances are present, but this too ideal. Certain tensor-based methods for handing incomplete multi-view data have emerged and have achieved better result. However, there are still some problems, such as use of traditional tensor norm which makes the computation high and is not able to handle out-of-sample. To solve these two problems, we proposed a new incomplete multi view learning method. A new tensor norm is defined to implement graph tensor data recover. The recovered graphs are then regularized to a consistent low-dimensional representation of the samples. In addition, adaptive weights are equipped to each view to adjust the importance of different views. Compared with the existing methods, our method nor only explores the consistency among views, but also obtains the low-dimensional representation of the new samples by using the learned projection matrix. An efficient algorithm based on inexact augmented Lagrange multiplier (ALM) method are designed to solve the model and convergence is proved. Experimental results on four datasets show the effectiveness of our method.

On Well-posedness and Minimax Optimal Rates of Nonparametric Q-function Estimation in Off-policy Evaluation

We study the off-policy evaluation (OPE) problem in an infinite-horizon Markov decision process with continuous states and actions. We recast the $Q$-function estimation into a special form of the nonparametric instrumental variables (NPIV) estimation problem. We first show that under one mild condition the NPIV formulation of $Q$-function estimation is well-posed in the sense of $L^2$-measure of ill-posedness with respect to the data generating distribution, bypassing a strong assumption on the discount factor $\gamma$ imposed in the recent literature for obtaining the $L^2$ convergence rates of various $Q$-function estimators. Thanks to this new well-posed property, we derive the first minimax lower bounds for the convergence rates of nonparametric estimation of $Q$-function and its derivatives in both sup-norm and $L^2$-norm, which are shown to be the same as those for the classical nonparametric regression (Stone, 1982). We then propose a sieve two-stage least squares estimator and establish its rate-optimality in both norms under some mild conditions. Our general results on the well-posedness and the minimax lower bounds are of independent interest to study not only other nonparametric estimators for $Q$-function but also efficient estimation on the value of any target policy in off-policy settings.

Efficient Estimation in NPIV Models: A Comparison of Various Neural Networks-Based Estimators

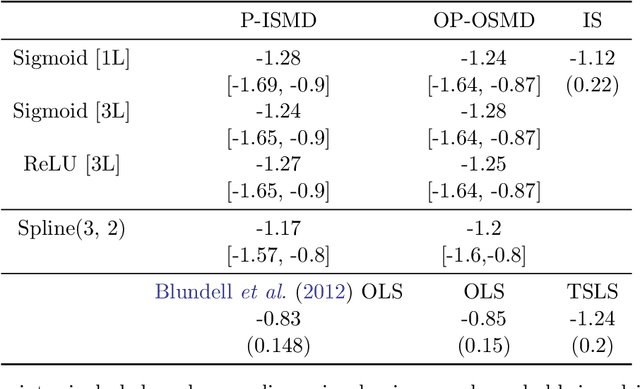
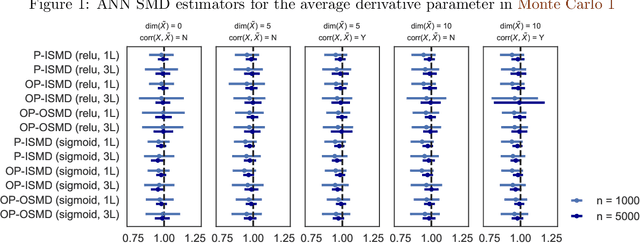
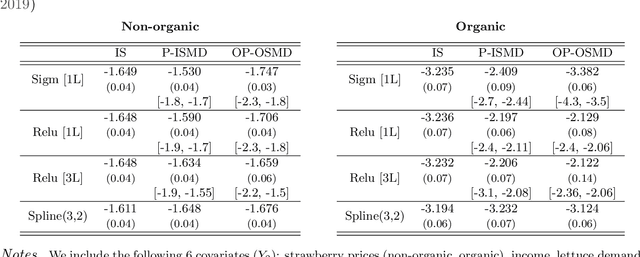
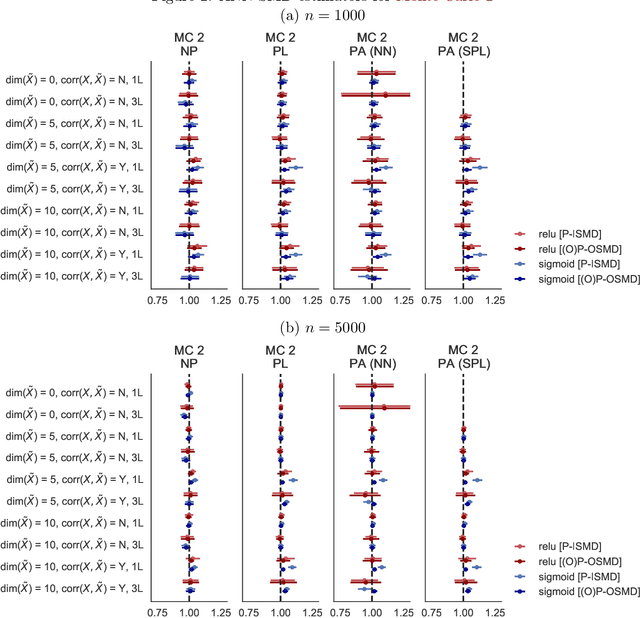
We investigate the computational performance of Artificial Neural Networks (ANNs) in semi-nonparametric instrumental variables (NPIV) models of high dimensional covariates that are relevant to empirical work in economics. We focus on efficient estimation of and inference on expectation functionals (such as weighted average derivatives) and use optimal criterion-based procedures (sieve minimum distance or SMD) and novel efficient score-based procedures (ES). Both these procedures use ANN to approximate the unknown function. Then, we provide a detailed practitioner's recipe for implementing these two classes of estimators. This involves the choice of tuning parameters both for the unknown functions (that include conditional expectations) but also for the choice of estimation of the optimal weights in SMD and the Riesz representers used with the ES estimators. Finally, we conduct a large set of Monte Carlo experiments that compares the finite-sample performance in complicated designs that involve a large set of regressors (up to 13 continuous), and various underlying nonlinearities and covariate correlations. Some of the takeaways from our results include: 1) tuning and optimization are delicate especially as the problem is nonconvex; 2) various architectures of the ANNs do not seem to matter for the designs we consider and given proper tuning, ANN methods perform well; 3) stable inferences are more difficult to achieve with ANN estimators; 4) optimal SMD based estimators perform adequately; 5) there seems to be a gap between implementation and approximation theory. Finally, we apply ANN NPIV to estimate average price elasticity and average derivatives in two demand examples.

Adaptive Estimation and Uniform Confidence Bands for Nonparametric IV

We introduce computationally simple, data-driven procedures for estimation and inference on a structural function $h_0$ and its derivatives in nonparametric models using instrumental variables. Our first procedure is a bootstrap-based, data-driven choice of sieve dimension for sieve nonparametric instrumental variables (NPIV) estimators. When implemented with this data-driven choice, sieve NPIV estimators of $h_0$ and its derivatives are adaptive: they converge at the best possible (i.e., minimax) sup-norm rate, without having to know the smoothness of $h_0$, degree of endogeneity of the regressors, or instrument strength. Our second procedure is a data-driven approach for constructing honest and adaptive uniform confidence bands (UCBs) for $h_0$ and its derivatives. Our data-driven UCBs guarantee coverage for $h_0$ and its derivatives uniformly over a generic class of data-generating processes (honesty) and contract at, or within a logarithmic factor of, the minimax sup-norm rate (adaptivity). As such, our data-driven UCBs deliver asymptotic efficiency gains relative to UCBs constructed via the usual approach of undersmoothing. In addition, both our procedures apply to nonparametric regression as a special case. We use our procedures to estimate and perform inference on a nonparametric gravity equation for the intensive margin of firm exports and find evidence against common parameterizations of the distribution of unobserved firm productivity.

Adaptive Estimation of Quadratic Functionals in Nonparametric Instrumental Variable Models

This paper considers adaptive estimation of quadratic functionals in the nonparametric instrumental variables (NPIV) models. Minimax estimation of a quadratic functional of a NPIV is an important problem in optimal estimation of a nonlinear functional of an ill-posed inverse regression with an unknown operator using one random sample. We first show that a leave-one-out, sieve NPIV estimator of the quadratic functional proposed by \cite{BC2020} attains a convergence rate that coincides with the lower bound previously derived by \cite{ChenChristensen2017}. The minimax rate is achieved by the optimal choice of a key tuning parameter (sieve dimension) that depends on unknown NPIV model features. We next propose a data driven choice of the tuning parameter based on Lepski's method. The adaptive estimator attains the minimax optimal rate in the severely ill-posed case and in the regular, mildly ill-posed case, but up to a multiplicative $\sqrt{\log n}$ in the irregular, mildly ill-posed case.