Myung Hwan Seo
SGMM: Stochastic Approximation to Generalized Method of Moments
Aug 25, 2023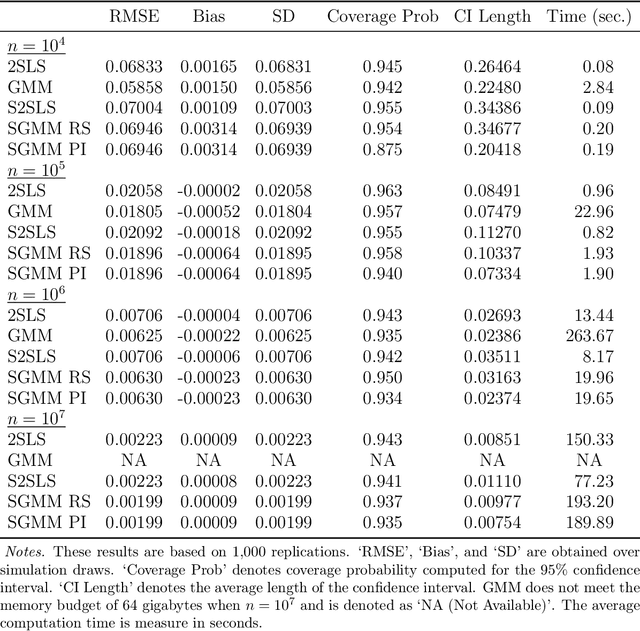
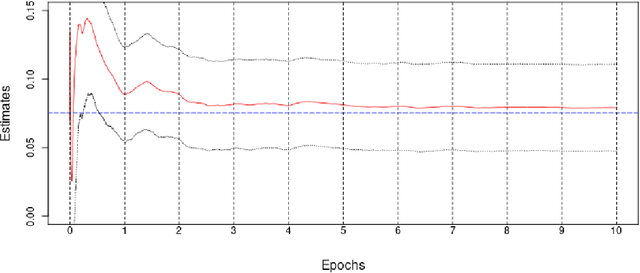
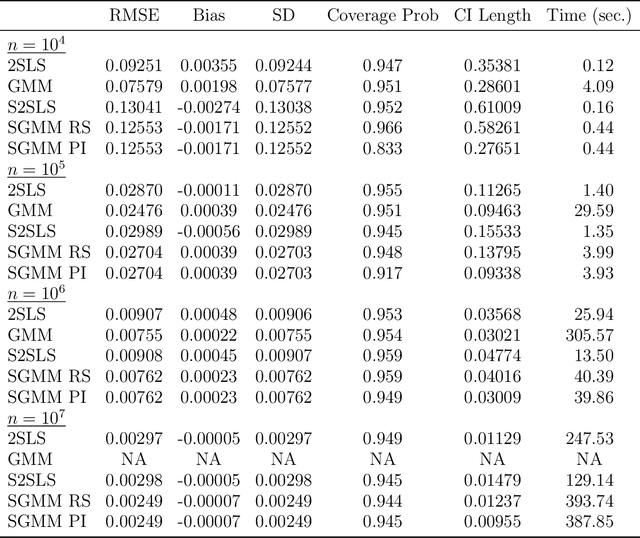
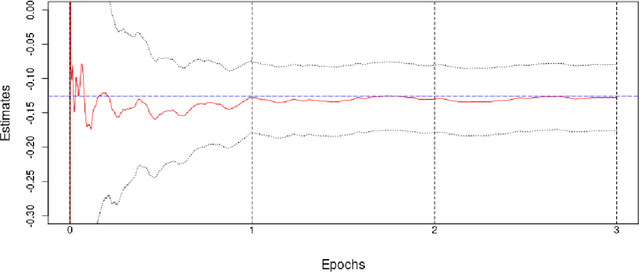
Abstract:We introduce a new class of algorithms, Stochastic Generalized Method of Moments (SGMM), for estimation and inference on (overidentified) moment restriction models. Our SGMM is a novel stochastic approximation alternative to the popular Hansen (1982) (offline) GMM, and offers fast and scalable implementation with the ability to handle streaming datasets in real time. We establish the almost sure convergence, and the (functional) central limit theorem for the inefficient online 2SLS and the efficient SGMM. Moreover, we propose online versions of the Durbin-Wu-Hausman and Sargan-Hansen tests that can be seamlessly integrated within the SGMM framework. Extensive Monte Carlo simulations show that as the sample size increases, the SGMM matches the standard (offline) GMM in terms of estimation accuracy and gains over computational efficiency, indicating its practical value for both large-scale and online datasets. We demonstrate the efficacy of our approach by a proof of concept using two well known empirical examples with large sample sizes.
Fast and Robust Online Inference with Stochastic Gradient Descent via Random Scaling
Jun 21, 2021
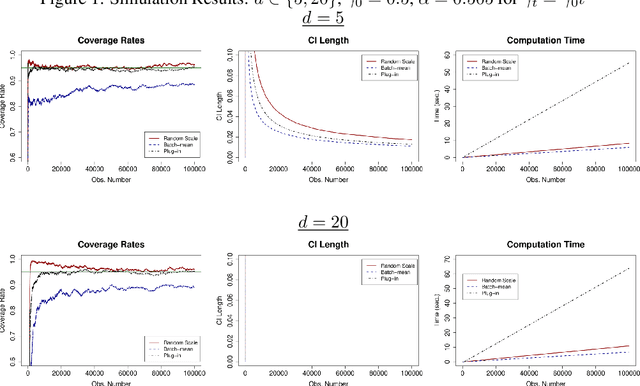
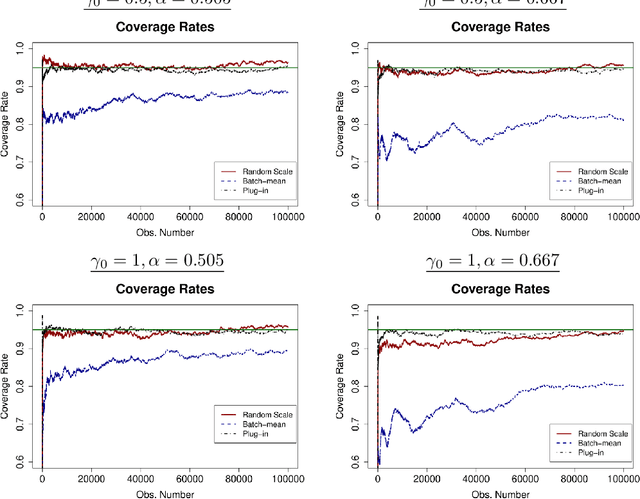
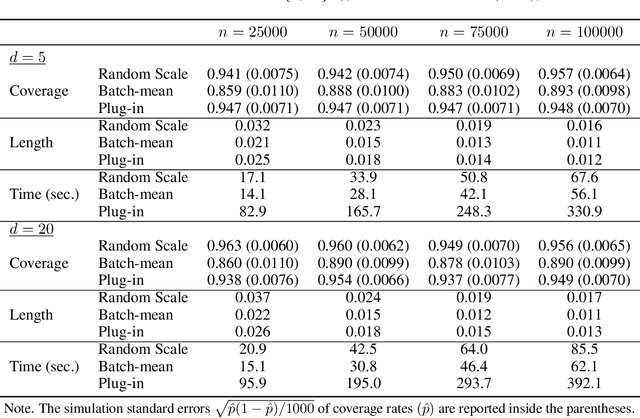
Abstract:We develop a new method of online inference for a vector of parameters estimated by the Polyak-Ruppert averaging procedure of stochastic gradient descent (SGD) algorithms. We leverage insights from time series regression in econometrics and construct asymptotically pivotal statistics via random scaling. Our approach is fully operational with online data and is rigorously underpinned by a functional central limit theorem. Our proposed inference method has a couple of key advantages over the existing methods. First, the test statistic is computed in an online fashion with only SGD iterates and the critical values can be obtained without any resampling methods, thereby allowing for efficient implementation suitable for massive online data. Second, there is no need to estimate the asymptotic variance and our inference method is shown to be robust to changes in the tuning parameters for SGD algorithms in simulation experiments with synthetic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge