Group Shapley Value and Counterfactual Simulations in a Structural Model

We propose a variant of the Shapley value, the group Shapley value, to interpret counterfactual simulations in structural economic models by quantifying the importance of different components. Our framework compares two sets of parameters, partitioned into multiple groups, and applying group Shapley value decomposition yields unique additive contributions to the changes between these sets. The relative contributions sum to one, enabling us to generate an importance table that is as easily interpretable as a regression table. The group Shapley value can be characterized as the solution to a constrained weighted least squares problem. Using this property, we develop robust decomposition methods to address scenarios where inputs for the group Shapley value are missing. We first apply our methodology to a simple Roy model and then illustrate its usefulness by revisiting two published papers.

SGMM: Stochastic Approximation to Generalized Method of Moments

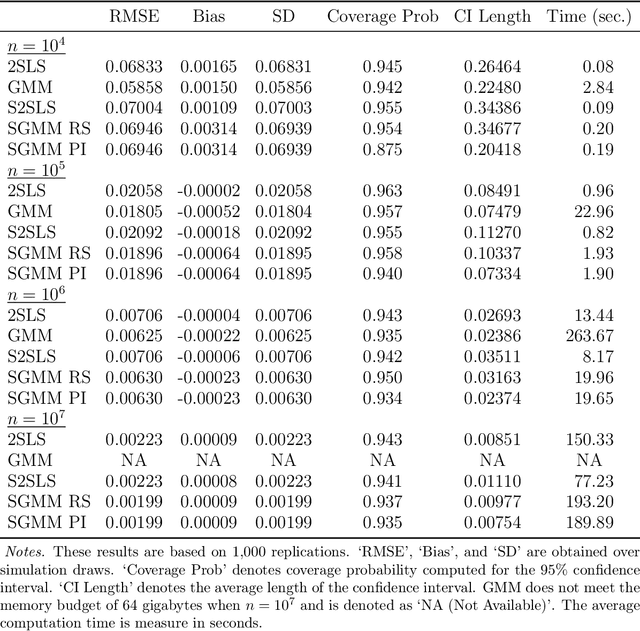
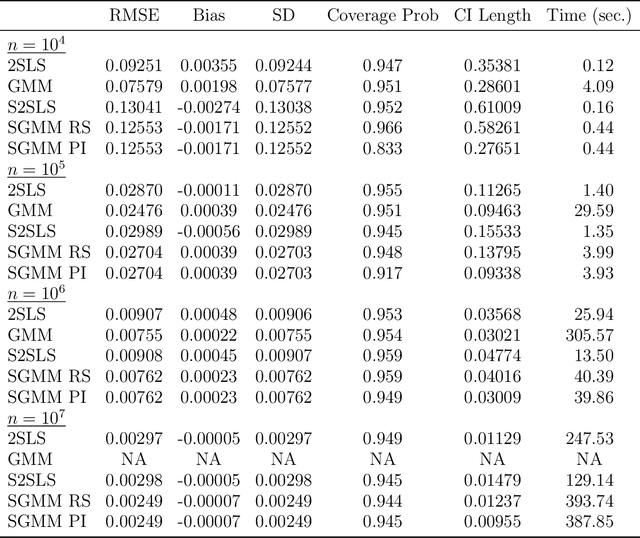
We introduce a new class of algorithms, Stochastic Generalized Method of Moments (SGMM), for estimation and inference on (overidentified) moment restriction models. Our SGMM is a novel stochastic approximation alternative to the popular Hansen (1982) (offline) GMM, and offers fast and scalable implementation with the ability to handle streaming datasets in real time. We establish the almost sure convergence, and the (functional) central limit theorem for the inefficient online 2SLS and the efficient SGMM. Moreover, we propose online versions of the Durbin-Wu-Hausman and Sargan-Hansen tests that can be seamlessly integrated within the SGMM framework. Extensive Monte Carlo simulations show that as the sample size increases, the SGMM matches the standard (offline) GMM in terms of estimation accuracy and gains over computational efficiency, indicating its practical value for both large-scale and online datasets. We demonstrate the efficacy of our approach by a proof of concept using two well known empirical examples with large sample sizes.

The Mean Squared Error of the Ridgeless Least Squares Estimator under General Assumptions on Regression Errors

In recent years, there has been a significant growth in research focusing on minimum $\ell_2$ norm (ridgeless) interpolation least squares estimators. However, the majority of these analyses have been limited to a simple regression error structure, assuming independent and identically distributed errors with zero mean and common variance, independent of the feature vectors. Additionally, the main focus of these theoretical analyses has been on the out-of-sample prediction risk. This paper breaks away from the existing literature by examining the mean squared error of the ridgeless interpolation least squares estimator, allowing for more general assumptions about the regression errors. Specifically, we investigate the potential benefits of overparameterization by characterizing the mean squared error in a finite sample. Our findings reveal that including a large number of unimportant parameters relative to the sample size can effectively reduce the mean squared error of the estimator. Notably, we establish that the estimation difficulties associated with the variance term can be summarized through the trace of the variance-covariance matrix of the regression errors.

Average Adjusted Association: Efficient Estimation with High Dimensional Confounders

The log odds ratio is a common parameter to measure association between (binary) outcome and exposure variables. Much attention has been paid to its parametric but robust estimation, or its nonparametric estimation as a function of confounders. However, discussion on how to use a summary statistic by averaging the log odds ratio function is surprisingly difficult to find despite the popularity and importance of averaging in other contexts such as estimating the average treatment effect. We propose a couple of efficient double/debiased machine learning (DML) estimators of the average log odds ratio, where the odds ratios are adjusted for observed (potentially high dimensional) confounders and are averaged over them. The estimators are built from two equivalent forms of the efficient influence function. The first estimator uses a prospective probability of the outcome conditional on the exposure and confounders; the second one employs a retrospective probability of the exposure conditional on the outcome and confounders. Our framework encompasses random sampling as well as outcome-based or exposure-based sampling. Finally, we illustrate how to apply the proposed estimators using real data.

Fast and Robust Online Inference with Stochastic Gradient Descent via Random Scaling

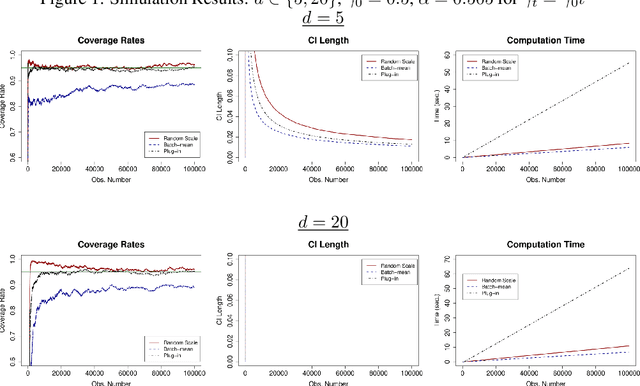
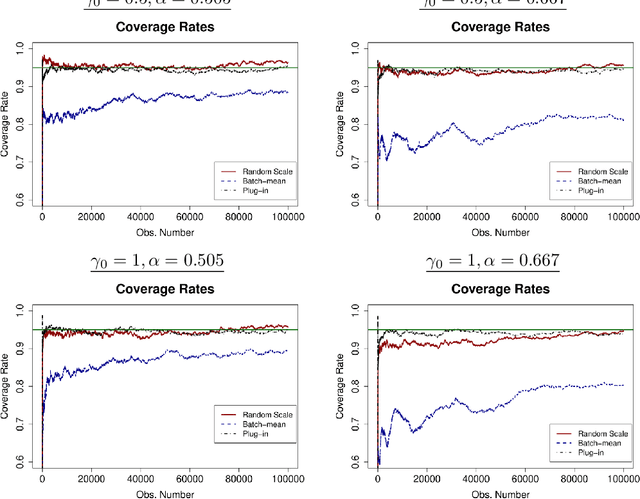
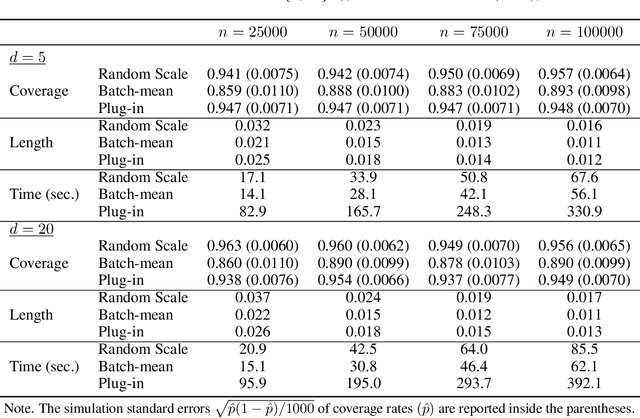
We develop a new method of online inference for a vector of parameters estimated by the Polyak-Ruppert averaging procedure of stochastic gradient descent (SGD) algorithms. We leverage insights from time series regression in econometrics and construct asymptotically pivotal statistics via random scaling. Our approach is fully operational with online data and is rigorously underpinned by a functional central limit theorem. Our proposed inference method has a couple of key advantages over the existing methods. First, the test statistic is computed in an online fashion with only SGD iterates and the critical values can be obtained without any resampling methods, thereby allowing for efficient implementation suitable for massive online data. Second, there is no need to estimate the asymptotic variance and our inference method is shown to be robust to changes in the tuning parameters for SGD algorithms in simulation experiments with synthetic data.

Sketching for Two-Stage Least Squares Estimation

When there is so much data that they become a computation burden, it is not uncommon to compute quantities of interest using a sketch of data of size $m$ instead of the full sample of size $n$. This paper investigates the implications for two-stage least squares (2SLS) estimation when the sketches are obtained by a computationally efficient method known as CountSketch. We obtain three results. First, we establish conditions under which given the full sample, a sketched 2SLS estimate can be arbitrarily close to the full-sample 2SLS estimate with high probability. Second, we give conditions under which the sketched 2SLS estimator converges in probability to the true parameter at a rate of $m^{-1/2}$ and is asymptotically normal. Third, we show that the asymptotic variance can be consistently estimated using the sketched sample and suggest methods for determining an inference-conscious sketch size $m$. The sketched 2SLS estimator is used to estimate returns to education.

Causal Inference in Case-Control Studies

We investigate identification of causal parameters in case-control and related studies. The odds ratio in the sample is our main estimand of interest and we articulate its relationship with causal parameters under various scenarios. It turns out that the odds ratio is generally a sharp upper bound for counterfactual relative risk under some monotonicity assumptions, without resorting to strong ignorability, nor to the rare-disease assumption. Further, we propose semparametrically efficient, easy-to-implement, machine-learning-friendly estimators of the aggregated (log) odds ratio by exploiting an explicit form of the efficient influence function. Using our new estimators, we develop methods for causal inference and illustrate the usefulness of our methods by a real-data example.

High Dimensional Classification through $\ell_0$-Penalized Empirical Risk Minimization

We consider a high dimensional binary classification problem and construct a classification procedure by minimizing the empirical misclassification risk with a penalty on the number of selected features. We derive non-asymptotic probability bounds on the estimated sparsity as well as on the excess misclassification risk. In particular, we show that our method yields a sparse solution whose l0-norm can be arbitrarily close to true sparsity with high probability and obtain the rates of convergence for the excess misclassification risk. The proposed procedure is implemented via the method of mixed integer linear programming. Its numerical performance is illustrated in Monte Carlo experiments.