The Mean Squared Error of the Ridgeless Least Squares Estimator under General Assumptions on Regression Errors

In recent years, there has been a significant growth in research focusing on minimum $\ell_2$ norm (ridgeless) interpolation least squares estimators. However, the majority of these analyses have been limited to a simple regression error structure, assuming independent and identically distributed errors with zero mean and common variance, independent of the feature vectors. Additionally, the main focus of these theoretical analyses has been on the out-of-sample prediction risk. This paper breaks away from the existing literature by examining the mean squared error of the ridgeless interpolation least squares estimator, allowing for more general assumptions about the regression errors. Specifically, we investigate the potential benefits of overparameterization by characterizing the mean squared error in a finite sample. Our findings reveal that including a large number of unimportant parameters relative to the sample size can effectively reduce the mean squared error of the estimator. Notably, we establish that the estimation difficulties associated with the variance term can be summarized through the trace of the variance-covariance matrix of the regression errors.

Bridged Adversarial Training

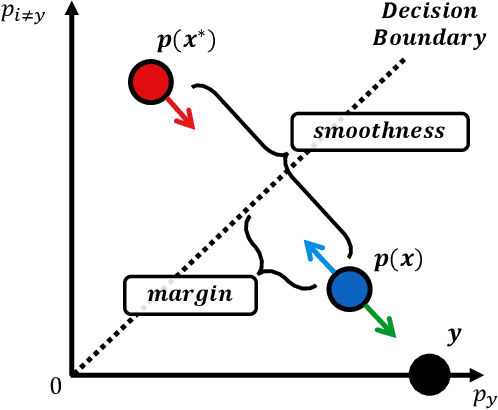
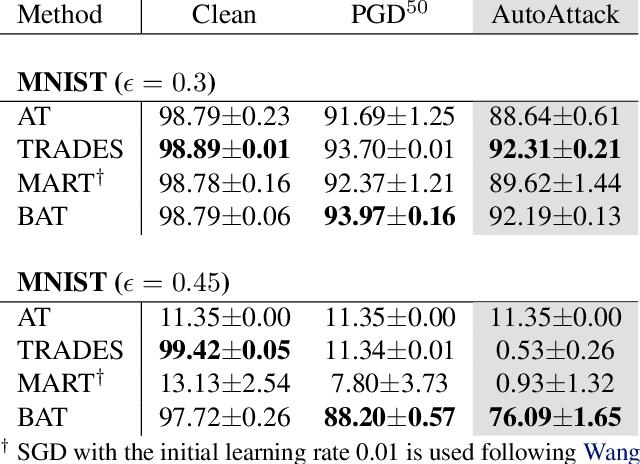
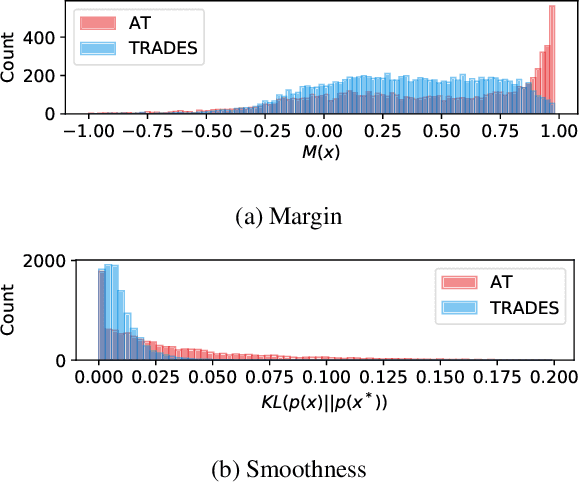
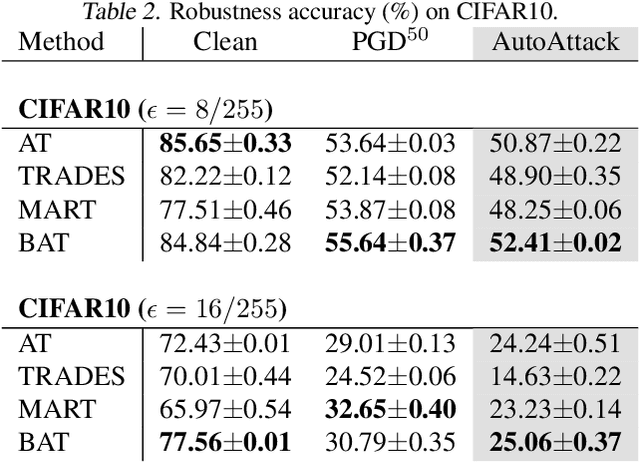
Adversarial robustness is considered as a required property of deep neural networks. In this study, we discover that adversarially trained models might have significantly different characteristics in terms of margin and smoothness, even they show similar robustness. Inspired by the observation, we investigate the effect of different regularizers and discover the negative effect of the smoothness regularizer on maximizing the margin. Based on the analyses, we propose a new method called bridged adversarial training that mitigates the negative effect by bridging the gap between clean and adversarial examples. We provide theoretical and empirical evidence that the proposed method provides stable and better robustness, especially for large perturbations.

GradDiv: Adversarial Robustness of Randomized Neural Networks via Gradient Diversity Regularization

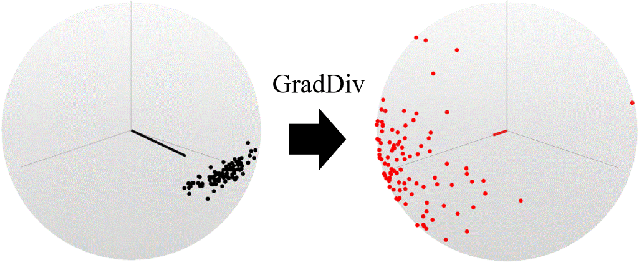
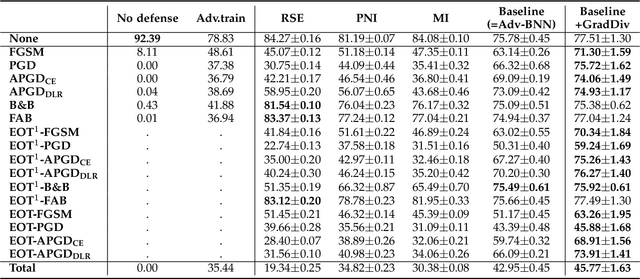
Deep learning is vulnerable to adversarial examples. Many defenses based on randomized neural networks have been proposed to solve the problem, but fail to achieve robustness against attacks using proxy gradients such as the Expectation over Transformation (EOT) attack. We investigate the effect of the adversarial attacks using proxy gradients on randomized neural networks and demonstrate that it highly relies on the directional distribution of the loss gradients of the randomized neural network. We show in particular that proxy gradients are less effective when the gradients are more scattered. To this end, we propose Gradient Diversity (GradDiv) regularizations that minimize the concentration of the gradients to build a robust randomized neural network. Our experiments on MNIST, CIFAR10, and STL10 show that our proposed GradDiv regularizations improve the adversarial robustness of randomized neural networks against a variety of state-of-the-art attack methods. Moreover, our method efficiently reduces the transferability among sample models of randomized neural networks.