Efficient Estimation in NPIV Models: A Comparison of Various Neural Networks-Based Estimators

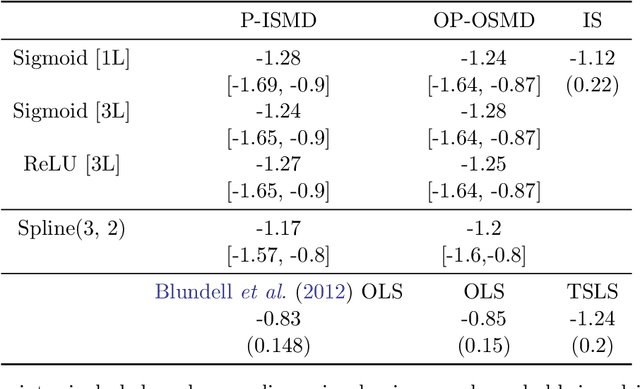
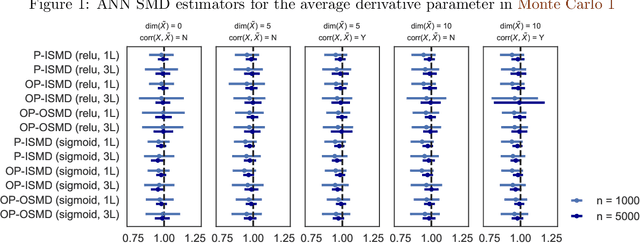
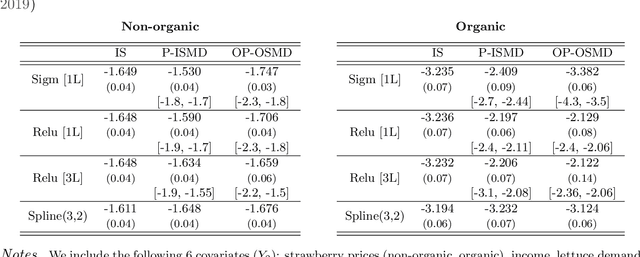
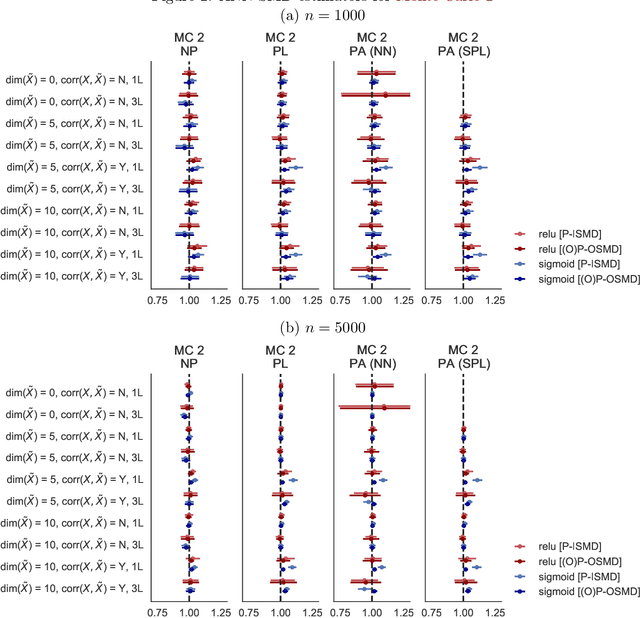
We investigate the computational performance of Artificial Neural Networks (ANNs) in semi-nonparametric instrumental variables (NPIV) models of high dimensional covariates that are relevant to empirical work in economics. We focus on efficient estimation of and inference on expectation functionals (such as weighted average derivatives) and use optimal criterion-based procedures (sieve minimum distance or SMD) and novel efficient score-based procedures (ES). Both these procedures use ANN to approximate the unknown function. Then, we provide a detailed practitioner's recipe for implementing these two classes of estimators. This involves the choice of tuning parameters both for the unknown functions (that include conditional expectations) but also for the choice of estimation of the optimal weights in SMD and the Riesz representers used with the ES estimators. Finally, we conduct a large set of Monte Carlo experiments that compares the finite-sample performance in complicated designs that involve a large set of regressors (up to 13 continuous), and various underlying nonlinearities and covariate correlations. Some of the takeaways from our results include: 1) tuning and optimization are delicate especially as the problem is nonconvex; 2) various architectures of the ANNs do not seem to matter for the designs we consider and given proper tuning, ANN methods perform well; 3) stable inferences are more difficult to achieve with ANN estimators; 4) optimal SMD based estimators perform adequately; 5) there seems to be a gap between implementation and approximation theory. Finally, we apply ANN NPIV to estimate average price elasticity and average derivatives in two demand examples.

Inference on Auctions with Weak Assumptions on Information

Given a sample of bids from independent auctions, this paper examines the question of inference on auction fundamentals (e.g. valuation distributions, welfare measures) under weak assumptions on information structure. The question is important as it allows us to learn about the valuation distribution in a robust way, i.e., without assuming that a particular information structure holds across observations. We leverage the recent contributions of \cite{Bergemann2013} in the robust mechanism design literature that exploit the link between Bayesian Correlated Equilibria and Bayesian Nash Equilibria in incomplete information games to construct an econometrics framework for learning about auction fundamentals using observed data on bids. We showcase our construction of identified sets in private value and common value auctions. Our approach for constructing these sets inherits the computational simplicity of solving for correlated equilibria: checking whether a particular valuation distribution belongs to the identified set is as simple as determining whether a {\it linear} program is feasible. A similar linear program can be used to construct the identified set on various welfare measures and counterfactual objects. For inference and to summarize statistical uncertainty, we propose novel finite sample methods using tail inequalities that are used to construct confidence regions on sets. We also highlight methods based on Bayesian bootstrap and subsampling. A set of Monte Carlo experiments show adequate finite sample properties of our inference procedures. We illustrate our methods using data from OCS auctions.