Jiafeng Chen
Optimal Conditional Inference in Adaptive Experiments
Sep 21, 2023Abstract:We study batched bandit experiments and consider the problem of inference conditional on the realized stopping time, assignment probabilities, and target parameter, where all of these may be chosen adaptively using information up to the last batch of the experiment. Absent further restrictions on the experiment, we show that inference using only the results of the last batch is optimal. When the adaptive aspects of the experiment are known to be location-invariant, in the sense that they are unchanged when we shift all batch-arm means by a constant, we show that there is additional information in the data, captured by one additional linear function of the batch-arm means. In the more restrictive case where the stopping time, assignment probabilities, and target parameter are known to depend on the data only through a collection of polyhedral events, we derive computationally tractable and optimal conditional inference procedures.
Synthetic Control As Online Linear Regression
Feb 17, 2022Abstract:This paper notes a simple connection between synthetic control and online learning. Specifically, we recognize synthetic control as an instance of Follow-The-Leader (FTL). Standard results in online convex optimization then imply that, even when outcomes are chosen by an adversary, synthetic control predictions of counterfactual outcomes for the treated unit perform almost as well as an oracle weighted average of control units' outcomes. Synthetic control on differenced data performs almost as well as oracle weighted difference-in-differences. We argue that this observation further supports the use of synthetic control estimators in comparative case studies.
Efficient Estimation in NPIV Models: A Comparison of Various Neural Networks-Based Estimators
Oct 14, 2021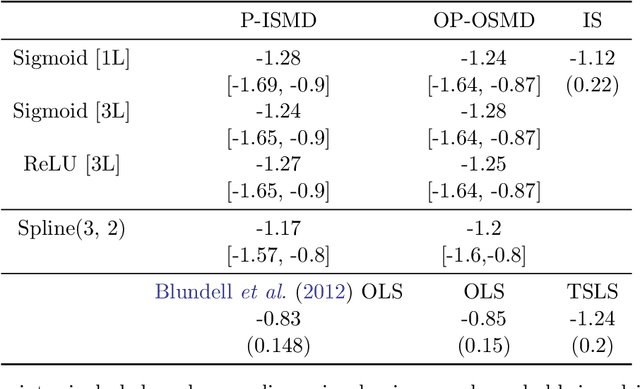
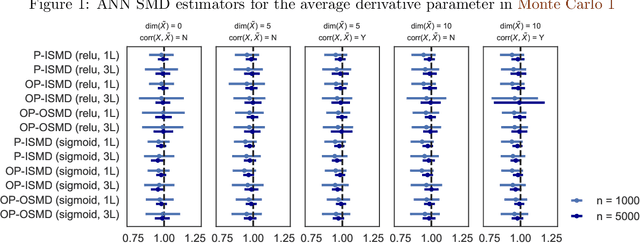
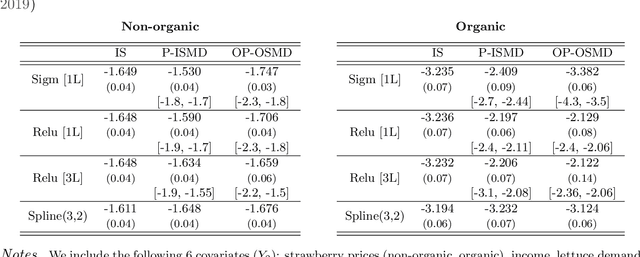
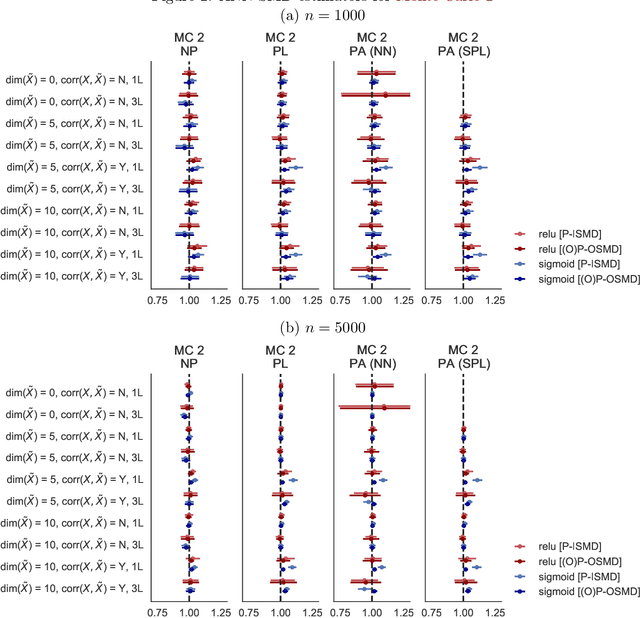
Abstract:We investigate the computational performance of Artificial Neural Networks (ANNs) in semi-nonparametric instrumental variables (NPIV) models of high dimensional covariates that are relevant to empirical work in economics. We focus on efficient estimation of and inference on expectation functionals (such as weighted average derivatives) and use optimal criterion-based procedures (sieve minimum distance or SMD) and novel efficient score-based procedures (ES). Both these procedures use ANN to approximate the unknown function. Then, we provide a detailed practitioner's recipe for implementing these two classes of estimators. This involves the choice of tuning parameters both for the unknown functions (that include conditional expectations) but also for the choice of estimation of the optimal weights in SMD and the Riesz representers used with the ES estimators. Finally, we conduct a large set of Monte Carlo experiments that compares the finite-sample performance in complicated designs that involve a large set of regressors (up to 13 continuous), and various underlying nonlinearities and covariate correlations. Some of the takeaways from our results include: 1) tuning and optimization are delicate especially as the problem is nonconvex; 2) various architectures of the ANNs do not seem to matter for the designs we consider and given proper tuning, ANN methods perform well; 3) stable inferences are more difficult to achieve with ANN estimators; 4) optimal SMD based estimators perform adequately; 5) there seems to be a gap between implementation and approximation theory. Finally, we apply ANN NPIV to estimate average price elasticity and average derivatives in two demand examples.
Mostly Harmless Machine Learning: Learning Optimal Instruments in Linear IV Models
Nov 12, 2020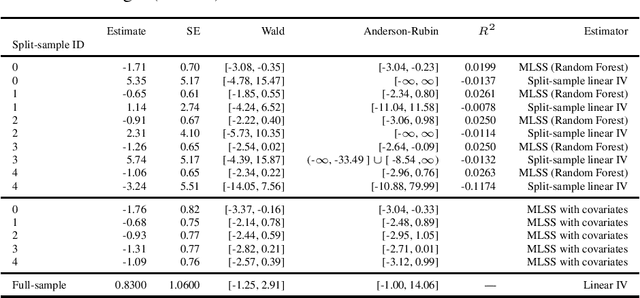
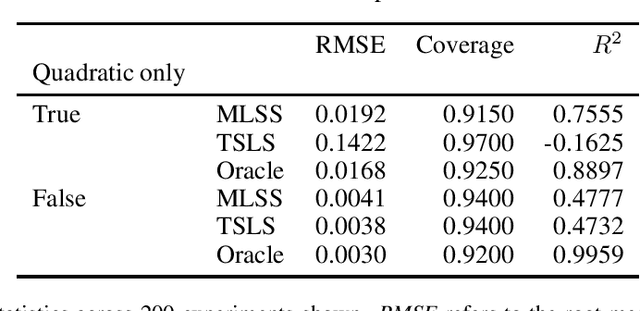
Abstract:We provide some simple theoretical results that justify incorporating machine learning in a standard linear instrumental variable setting, prevalent in empirical research in economics. Machine learning techniques, combined with sample-splitting, extract nonlinear variation in the instrument that may dramatically improve estimation precision and robustness by boosting instrument strength. The analysis is straightforward in the absence of covariates. The presence of linearly included exogenous covariates complicates identification, as the researcher would like to prevent nonlinearities in the covariates from providing the identifying variation. Our procedure can be effectively adapted to account for this complication, based on an argument by Chamberlain (1992). Our method preserves standard intuitions and interpretations of linear instrumental variable methods and provides a simple, user-friendly upgrade to the applied economics toolbox. We illustrate our method with an example in law and criminal justice, examining the causal effect of appellate court reversals on district court sentencing decisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge