Estimating the Long-Term Effects of Novel Treatments

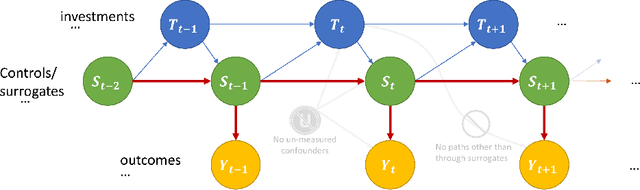
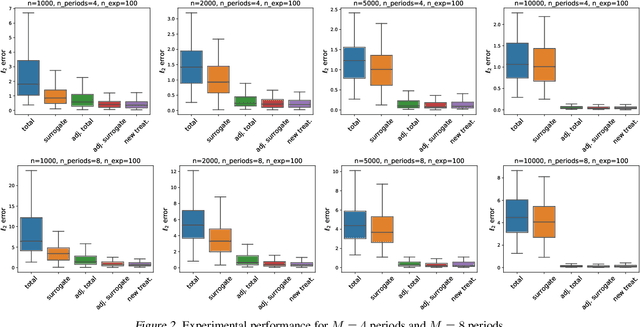
Policy makers typically face the problem of wanting to estimate the long-term effects of novel treatments, while only having historical data of older treatment options. We assume access to a long-term dataset where only past treatments were administered and a short-term dataset where novel treatments have been administered. We propose a surrogate based approach where we assume that the long-term effect is channeled through a multitude of available short-term proxies. Our work combines three major recent techniques in the causal machine learning literature: surrogate indices, dynamic treatment effect estimation and double machine learning, in a unified pipeline. We show that our method is consistent and provides root-n asymptotically normal estimates under a Markovian assumption on the data and the observational policy. We use a data-set from a major corporation that includes customer investments over a three year period to create a semi-synthetic data distribution where the major qualitative properties of the real dataset are preserved. We evaluate the performance of our method and discuss practical challenges of deploying our formal methodology and how to address them.

Mostly Harmless Machine Learning: Learning Optimal Instruments in Linear IV Models

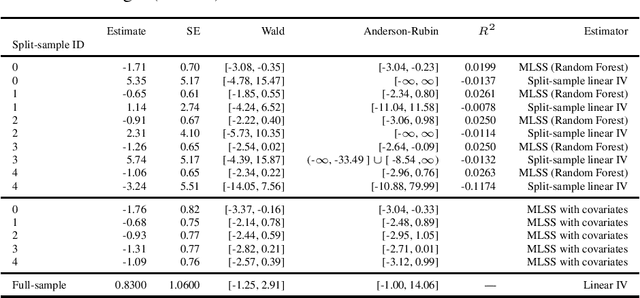
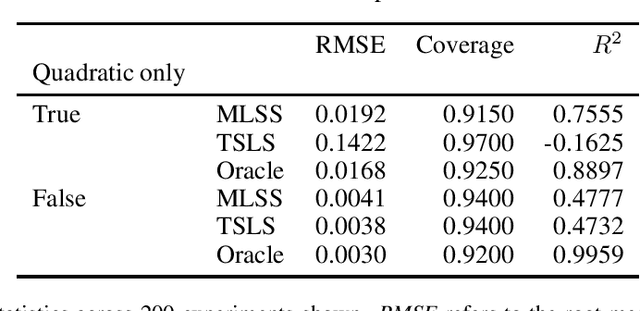
We provide some simple theoretical results that justify incorporating machine learning in a standard linear instrumental variable setting, prevalent in empirical research in economics. Machine learning techniques, combined with sample-splitting, extract nonlinear variation in the instrument that may dramatically improve estimation precision and robustness by boosting instrument strength. The analysis is straightforward in the absence of covariates. The presence of linearly included exogenous covariates complicates identification, as the researcher would like to prevent nonlinearities in the covariates from providing the identifying variation. Our procedure can be effectively adapted to account for this complication, based on an argument by Chamberlain (1992). Our method preserves standard intuitions and interpretations of linear instrumental variable methods and provides a simple, user-friendly upgrade to the applied economics toolbox. We illustrate our method with an example in law and criminal justice, examining the causal effect of appellate court reversals on district court sentencing decisions.

Minimax Estimation of Conditional Moment Models

We develop an approach for estimating models described via conditional moment restrictions, with a prototypical application being non-parametric instrumental variable regression. We introduce a min-max criterion function, under which the estimation problem can be thought of as solving a zero-sum game between a modeler who is optimizing over the hypothesis space of the target model and an adversary who identifies violating moments over a test function space. We analyze the statistical estimation rate of the resulting estimator for arbitrary hypothesis spaces, with respect to an appropriate analogue of the mean squared error metric, for ill-posed inverse problems. We show that when the minimax criterion is regularized with a second moment penalty on the test function and the test function space is sufficiently rich, then the estimation rate scales with the critical radius of the hypothesis and test function spaces, a quantity which typically gives tight fast rates. Our main result follows from a novel localized Rademacher analysis of statistical learning problems defined via minimax objectives. We provide applications of our main results for several hypothesis spaces used in practice such as: reproducing kernel Hilbert spaces, high dimensional sparse linear functions, spaces defined via shape constraints, ensemble estimators such as random forests, and neural networks. For each of these applications we provide computationally efficient optimization methods for solving the corresponding minimax problem (e.g. stochastic first-order heuristics for neural networks). In several applications, we show how our modified mean squared error rate, combined with conditions that bound the ill-posedness of the inverse problem, lead to mean squared error rates. We conclude with an extensive experimental analysis of the proposed methods.

Double/Debiased Machine Learning for Dynamic Treatment Effects

We consider the estimation of treatment effects in settings when multiple treatments are assigned over time and treatments can have a causal effect on future outcomes. We formulate the problem as a linear state space Markov process with a high dimensional state and propose an extension of the double/debiased machine learning framework to estimate the dynamic effects of treatments. Our method allows the use of arbitrary machine learning methods to control for the high dimensional state, subject to a mean square error guarantee, while still allowing parametric estimation and construction of confidence intervals for the dynamic treatment effect parameters of interest. Our method is based on a sequential regression peeling process, which we show can be equivalently interpreted as a Neyman orthogonal moment estimator. This allows us to show root-n asymptotic normality of the estimated causal effects.

Machine Learning Estimation of Heterogeneous Treatment Effects with Instruments

We consider the estimation of heterogeneous treatment effects with arbitrary machine learning methods in the presence of unobserved confounders with the aid of a valid instrument. Such settings arise in A/B tests with an intent-to-treat structure, where the experimenter randomizes over which user will receive a recommendation to take an action, and we are interested in the effect of the downstream action. We develop a statistical learning approach to the estimation of heterogeneous effects, reducing the problem to the minimization of an appropriate loss function that depends on a set of auxiliary models (each corresponding to a separate prediction task). The reduction enables the use of all recent algorithmic advances (e.g. neural nets, forests). We show that the estimated effect model is robust to estimation errors in the auxiliary models, by showing that the loss satisfies a Neyman orthogonality criterion. Our approach can be used to estimate projections of the true effect model on simpler hypothesis spaces. When these spaces are parametric, then the parameter estimates are asymptotically normal, which enables construction of confidence sets. We applied our method to estimate the effect of membership on downstream webpage engagement on TripAdvisor, using as an instrument an intent-to-treat A/B test among 4 million TripAdvisor users, where some users received an easier membership sign-up process. We also validate our method on synthetic data and on public datasets for the effects of schooling on income.

Semi-Parametric Efficient Policy Learning with Continuous Actions

We consider off-policy evaluation and optimization with continuous action spaces. We focus on observational data where the data collection policy is unknown and needs to be estimated. We take a semi-parametric approach where the value function takes a known parametric form in the treatment, but we are agnostic on how it depends on the observed contexts. We propose a doubly robust off-policy estimate for this setting and show that off-policy optimization based on this estimate is robust to estimation errors of the policy function or the regression model. Our results also apply if the model does not satisfy our semi-parametric form, but rather we measure regret in terms of the best projection of the true value function to this functional space. Our work extends prior approaches of policy optimization from observational data that only considered discrete actions. We provide an experimental evaluation of our method in a synthetic data example motivated by optimal personalized pricing and costly resource allocation.

Non-Parametric Inference Adaptive to Intrinsic Dimension

We consider non-parametric estimation and inference of conditional moment models in high dimensions. We show that even when the dimension $D$ of the conditioning variable is larger than the sample size $n$, estimation and inference is feasible as long as the distribution of the conditioning variable has small intrinsic dimension $d$, as measured by the doubling dimension. Our estimation is based on a sub-sampled ensemble of the $k$-nearest neighbors $Z$-estimator. We show that if the intrinsic dimension of the co-variate distribution is equal to $d$, then the finite sample estimation error of our estimator is of order $n^{-1/(d+2)}$ and our estimate is $n^{1/(d+2)}$-asymptotically normal, irrespective of $D$. We discuss extensions and applications to heterogeneous treatment effect estimation.

Adversarial Generalized Method of Moments

We provide an approach for learning deep neural net representations of models described via conditional moment restrictions. Conditional moment restrictions are widely used, as they are the language by which social scientists describe the assumptions they make to enable causal inference. We formulate the problem of estimating the underling model as a zero-sum game between a modeler and an adversary and apply adversarial training. Our approach is similar in nature to Generative Adversarial Networks (GAN), though here the modeler is learning a representation of a function that satisfies a continuum of moment conditions and the adversary is identifying violating moments. We outline ways of constructing effective adversaries in practice, including kernels centered by k-means clustering, and random forests. We examine the practical performance of our approach in the setting of non-parametric instrumental variable regression.

Counterfactual Prediction with Deep Instrumental Variables Networks

We are in the middle of a remarkable rise in the use and capability of artificial intelligence. Much of this growth has been fueled by the success of deep learning architectures: models that map from observables to outputs via multiple layers of latent representations. These deep learning algorithms are effective tools for unstructured prediction, and they can be combined in AI systems to solve complex automated reasoning problems. This paper provides a recipe for combining ML algorithms to solve for causal effects in the presence of instrumental variables -- sources of treatment randomization that are conditionally independent from the response. We show that a flexible IV specification resolves into two prediction tasks that can be solved with deep neural nets: a first-stage network for treatment prediction and a second-stage network whose loss function involves integration over the conditional treatment distribution. This Deep IV framework imposes some specific structure on the stochastic gradient descent routine used for training, but it is general enough that we can take advantage of off-the-shelf ML capabilities and avoid extensive algorithm customization. We outline how to obtain out-of-sample causal validation in order to avoid over-fit. We also introduce schemes for both Bayesian and frequentist inference: the former via a novel adaptation of dropout training, and the latter via a data splitting routine.