Victor Lei
Machine Learning Estimation of Heterogeneous Treatment Effects with Instruments
Jun 06, 2019
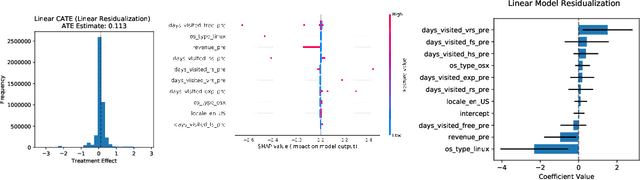
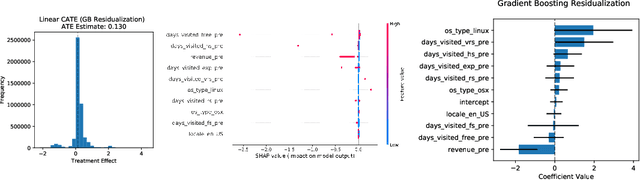
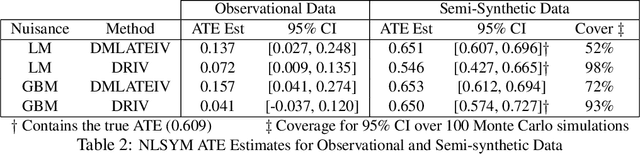
Abstract:We consider the estimation of heterogeneous treatment effects with arbitrary machine learning methods in the presence of unobserved confounders with the aid of a valid instrument. Such settings arise in A/B tests with an intent-to-treat structure, where the experimenter randomizes over which user will receive a recommendation to take an action, and we are interested in the effect of the downstream action. We develop a statistical learning approach to the estimation of heterogeneous effects, reducing the problem to the minimization of an appropriate loss function that depends on a set of auxiliary models (each corresponding to a separate prediction task). The reduction enables the use of all recent algorithmic advances (e.g. neural nets, forests). We show that the estimated effect model is robust to estimation errors in the auxiliary models, by showing that the loss satisfies a Neyman orthogonality criterion. Our approach can be used to estimate projections of the true effect model on simpler hypothesis spaces. When these spaces are parametric, then the parameter estimates are asymptotically normal, which enables construction of confidence sets. We applied our method to estimate the effect of membership on downstream webpage engagement on TripAdvisor, using as an instrument an intent-to-treat A/B test among 4 million TripAdvisor users, where some users received an easier membership sign-up process. We also validate our method on synthetic data and on public datasets for the effects of schooling on income.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge