Estimating the Long-Term Effects of Novel Treatments

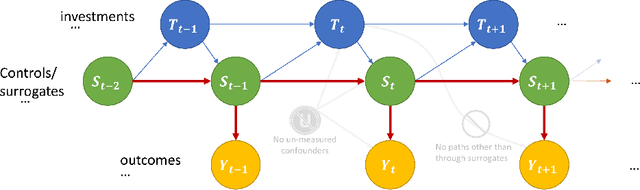
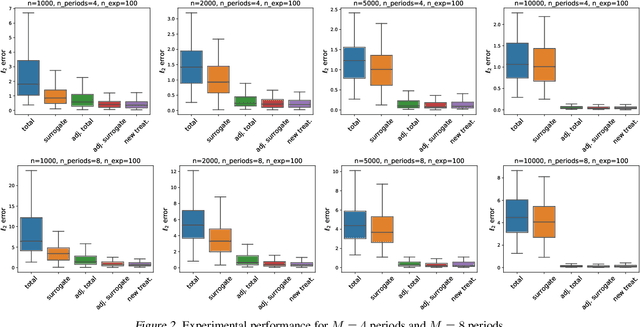
Policy makers typically face the problem of wanting to estimate the long-term effects of novel treatments, while only having historical data of older treatment options. We assume access to a long-term dataset where only past treatments were administered and a short-term dataset where novel treatments have been administered. We propose a surrogate based approach where we assume that the long-term effect is channeled through a multitude of available short-term proxies. Our work combines three major recent techniques in the causal machine learning literature: surrogate indices, dynamic treatment effect estimation and double machine learning, in a unified pipeline. We show that our method is consistent and provides root-n asymptotically normal estimates under a Markovian assumption on the data and the observational policy. We use a data-set from a major corporation that includes customer investments over a three year period to create a semi-synthetic data distribution where the major qualitative properties of the real dataset are preserved. We evaluate the performance of our method and discuss practical challenges of deploying our formal methodology and how to address them.

Machine Learning Estimation of Heterogeneous Treatment Effects with Instruments

We consider the estimation of heterogeneous treatment effects with arbitrary machine learning methods in the presence of unobserved confounders with the aid of a valid instrument. Such settings arise in A/B tests with an intent-to-treat structure, where the experimenter randomizes over which user will receive a recommendation to take an action, and we are interested in the effect of the downstream action. We develop a statistical learning approach to the estimation of heterogeneous effects, reducing the problem to the minimization of an appropriate loss function that depends on a set of auxiliary models (each corresponding to a separate prediction task). The reduction enables the use of all recent algorithmic advances (e.g. neural nets, forests). We show that the estimated effect model is robust to estimation errors in the auxiliary models, by showing that the loss satisfies a Neyman orthogonality criterion. Our approach can be used to estimate projections of the true effect model on simpler hypothesis spaces. When these spaces are parametric, then the parameter estimates are asymptotically normal, which enables construction of confidence sets. We applied our method to estimate the effect of membership on downstream webpage engagement on TripAdvisor, using as an instrument an intent-to-treat A/B test among 4 million TripAdvisor users, where some users received an easier membership sign-up process. We also validate our method on synthetic data and on public datasets for the effects of schooling on income.