A Meta-learner for Heterogeneous Effects in Difference-in-Differences

We address the problem of estimating heterogeneous treatment effects in panel data, adopting the popular Difference-in-Differences (DiD) framework under the conditional parallel trends assumption. We propose a novel doubly robust meta-learner for the Conditional Average Treatment Effect on the Treated (CATT), reducing the estimation to a convex risk minimization problem involving a set of auxiliary models. Our framework allows for the flexible estimation of the CATT, when conditioning on any subset of variables of interest using generic machine learning. Leveraging Neyman orthogonality, our proposed approach is robust to estimation errors in the auxiliary models. As a generalization to our main result, we develop a meta-learning approach for the estimation of general conditional functionals under covariate shift. We also provide an extension to the instrumented DiD setting with non-compliance. Empirical results demonstrate the superiority of our approach over existing baselines.

Estimating the Long-Term Effects of Novel Treatments

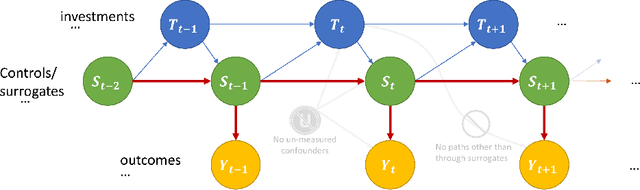
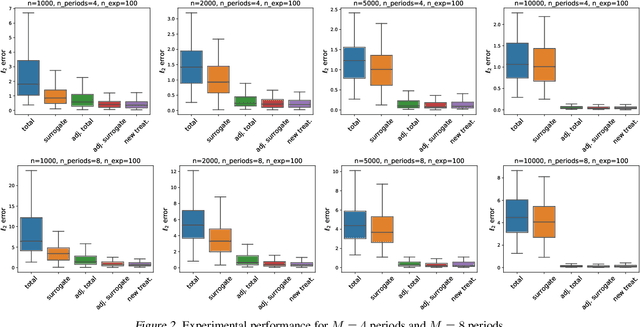
Policy makers typically face the problem of wanting to estimate the long-term effects of novel treatments, while only having historical data of older treatment options. We assume access to a long-term dataset where only past treatments were administered and a short-term dataset where novel treatments have been administered. We propose a surrogate based approach where we assume that the long-term effect is channeled through a multitude of available short-term proxies. Our work combines three major recent techniques in the causal machine learning literature: surrogate indices, dynamic treatment effect estimation and double machine learning, in a unified pipeline. We show that our method is consistent and provides root-n asymptotically normal estimates under a Markovian assumption on the data and the observational policy. We use a data-set from a major corporation that includes customer investments over a three year period to create a semi-synthetic data distribution where the major qualitative properties of the real dataset are preserved. We evaluate the performance of our method and discuss practical challenges of deploying our formal methodology and how to address them.