Regularized DeepIV with Model Selection

In this paper, we study nonparametric estimation of instrumental variable (IV) regressions. While recent advancements in machine learning have introduced flexible methods for IV estimation, they often encounter one or more of the following limitations: (1) restricting the IV regression to be uniquely identified; (2) requiring minimax computation oracle, which is highly unstable in practice; (3) absence of model selection procedure. In this paper, we present the first method and analysis that can avoid all three limitations, while still enabling general function approximation. Specifically, we propose a minimax-oracle-free method called Regularized DeepIV (RDIV) regression that can converge to the least-norm IV solution. Our method consists of two stages: first, we learn the conditional distribution of covariates, and by utilizing the learned distribution, we learn the estimator by minimizing a Tikhonov-regularized loss function. We further show that our method allows model selection procedures that can achieve the oracle rates in the misspecified regime. When extended to an iterative estimator, our method matches the current state-of-the-art convergence rate. Our method is a Tikhonov regularized variant of the popular DeepIV method with a non-parametric MLE first-stage estimator, and our results provide the first rigorous guarantees for this empirically used method, showcasing the importance of regularization which was absent from the original work.

Causal Q-Aggregation for CATE Model Selection

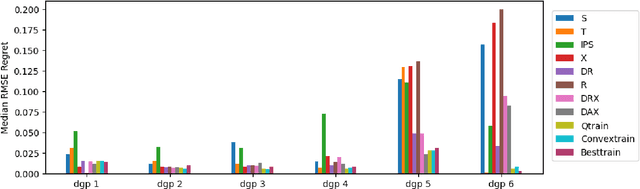
Accurate estimation of conditional average treatment effects (CATE) is at the core of personalized decision making. While there is a plethora of models for CATE estimation, model selection is a nontrivial task, due to the fundamental problem of causal inference. Recent empirical work provides evidence in favor of proxy loss metrics with double robust properties and in favor of model ensembling. However, theoretical understanding is lacking. Direct application of prior theoretical work leads to suboptimal oracle model selection rates due to the non-convexity of the model selection problem. We provide regret rates for the major existing CATE ensembling approaches and propose a new CATE model ensembling approach based on Q-aggregation using the doubly robust loss. Our main result shows that causal Q-aggregation achieves statistically optimal oracle model selection regret rates of $\frac{\log(M)}{n}$ (with $M$ models and $n$ samples), with the addition of higher-order estimation error terms related to products of errors in the nuisance functions. Crucially, our regret rate does not require that any of the candidate CATE models be close to the truth. We validate our new method on many semi-synthetic datasets and also provide extensions of our work to CATE model selection with instrumental variables and unobserved confounding.

Interpretable Predictive Models to Understand Risk Factors for Maternal and Fetal Outcomes

Although most pregnancies result in a good outcome, complications are not uncommon and can be associated with serious implications for mothers and babies. Predictive modeling has the potential to improve outcomes through better understanding of risk factors, heightened surveillance for high risk patients, and more timely and appropriate interventions, thereby helping obstetricians deliver better care. We identify and study the most important risk factors for four types of pregnancy complications: (i) severe maternal morbidity, (ii) shoulder dystocia, (iii) preterm preeclampsia, and (iv) antepartum stillbirth. We use an Explainable Boosting Machine (EBM), a high-accuracy glass-box learning method, for prediction and identification of important risk factors. We undertake external validation and perform an extensive robustness analysis of the EBM models. EBMs match the accuracy of other black-box ML methods such as deep neural networks and random forests, and outperform logistic regression, while being more interpretable. EBMs prove to be robust. The interpretability of the EBM models reveals surprising insights into the features contributing to risk (e.g. maternal height is the second most important feature for shoulder dystocia) and may have potential for clinical application in the prediction and prevention of serious complications in pregnancy.

Using Interpretable Machine Learning to Predict Maternal and Fetal Outcomes

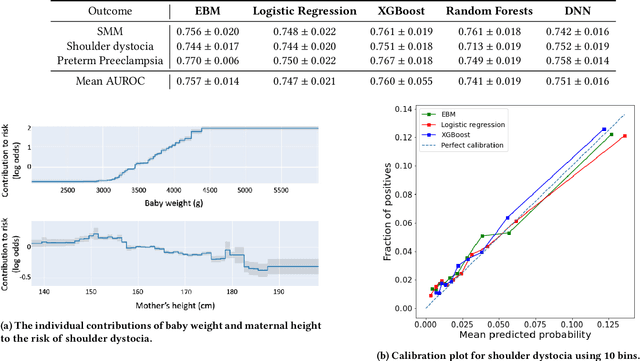
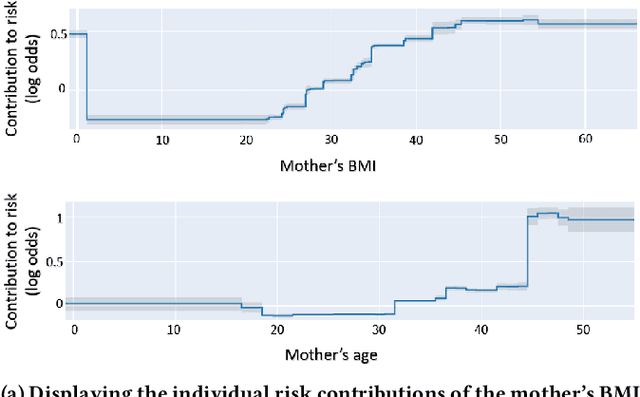
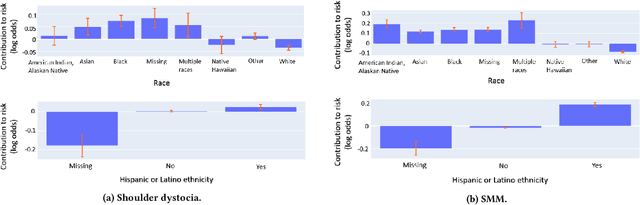
Most pregnancies and births result in a good outcome, but complications are not uncommon and when they do occur, they can be associated with serious implications for mothers and babies. Predictive modeling has the potential to improve outcomes through better understanding of risk factors, heightened surveillance, and more timely and appropriate interventions, thereby helping obstetricians deliver better care. For three types of complications we identify and study the most important risk factors using Explainable Boosting Machine (EBM), a glass box model, in order to gain intelligibility: (i) Severe Maternal Morbidity (SMM), (ii) shoulder dystocia, and (iii) preterm preeclampsia. While using the interpretability of EBM's to reveal surprising insights into the features contributing to risk, our experiments show EBMs match the accuracy of other black-box ML methods such as deep neural nets and random forests.