Semi-Parametric Efficient Policy Learning with Continuous Actions

We consider off-policy evaluation and optimization with continuous action spaces. We focus on observational data where the data collection policy is unknown and needs to be estimated. We take a semi-parametric approach where the value function takes a known parametric form in the treatment, but we are agnostic on how it depends on the observed contexts. We propose a doubly robust off-policy estimate for this setting and show that off-policy optimization based on this estimate is robust to estimation errors of the policy function or the regression model. Our results also apply if the model does not satisfy our semi-parametric form, but rather we measure regret in terms of the best projection of the true value function to this functional space. Our work extends prior approaches of policy optimization from observational data that only considered discrete actions. We provide an experimental evaluation of our method in a synthetic data example motivated by optimal personalized pricing and costly resource allocation.

Generic Machine Learning Inference on Heterogenous Treatment Effects in Randomized Experiments

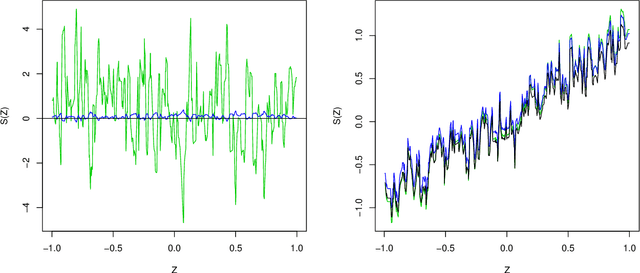
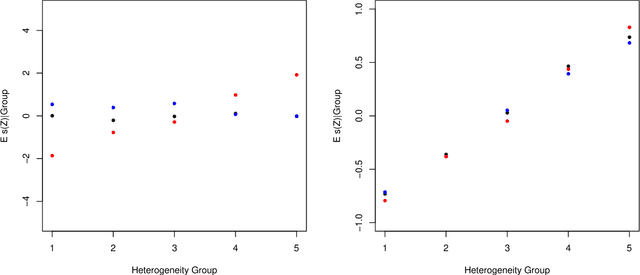
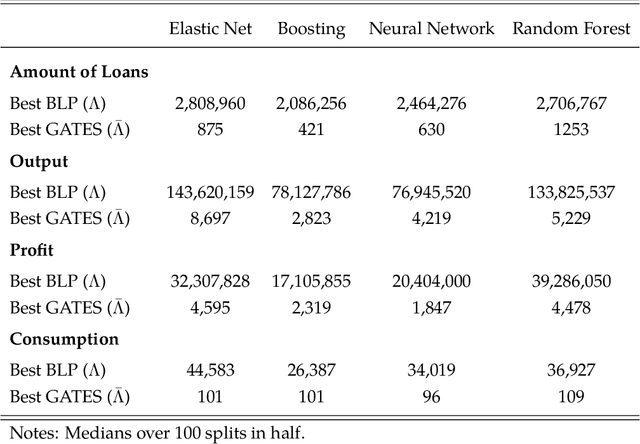
We propose strategies to estimate and make inference on key features of heterogeneous effects in randomized experiments. These key features include best linear predictors of the effects using machine learning proxies, average effects sorted by impact groups, and average characteristics of most and least impacted units. The approach is valid in high dimensional settings, where the effects are proxied by machine learning methods. We post-process these proxies into the estimates of the key features. Our approach is generic, it can be used in conjunction with penalized methods, deep and shallow neural networks, canonical and new random forests, boosted trees, and ensemble methods. Our approach is agnostic and does not make unrealistic or hard-to-check assumptions; we don't require conditions for consistency of the ML methods. Estimation and inference relies on repeated data splitting to avoid overfitting and achieve validity. For inference, we take medians of p-values and medians of confidence intervals, resulting from many different data splits, and then adjust their nominal level to guarantee uniform validity. This variational inference method is shown to be uniformly valid and quantifies the uncertainty coming from both parameter estimation and data splitting. The inference method could be of substantial independent interest in many machine learning applications. An empirical application to the impact of micro-credit on economic development illustrates the use of the approach in randomized experiments. An additional application to the impact of the gender discrimination on wages illustrates the potential use of the approach in observational studies, where machine learning methods can be used to condition flexibly on very high-dimensional controls.

Double/Debiased Machine Learning for Treatment and Causal Parameters

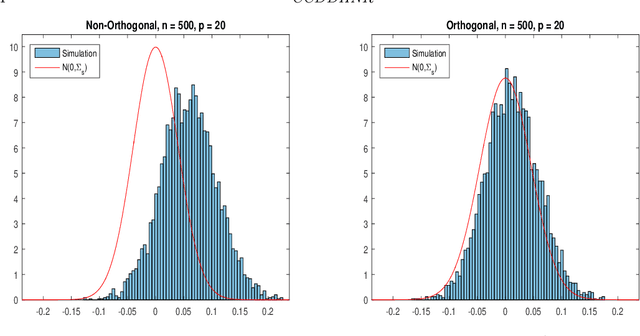
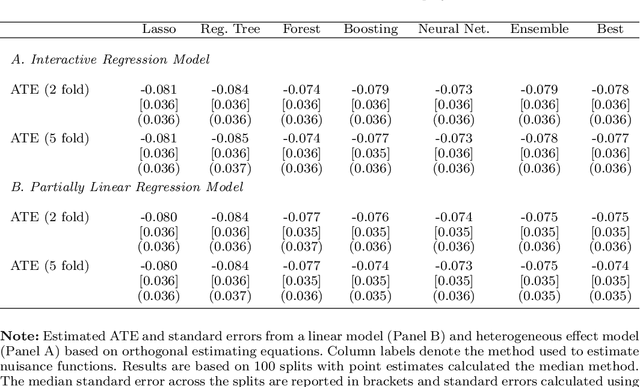
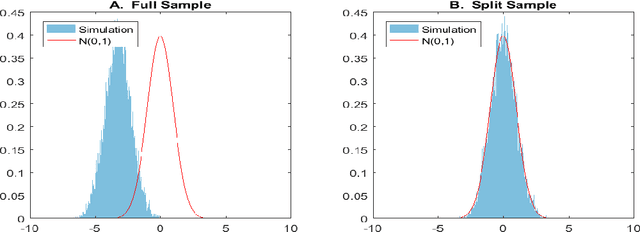
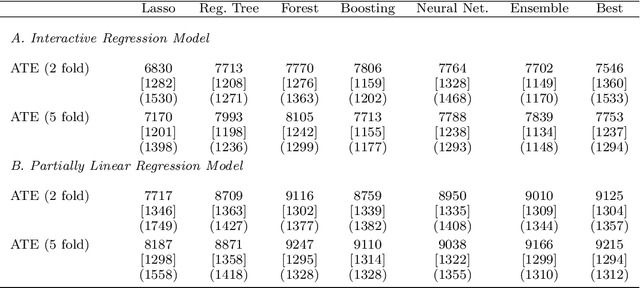
Most modern supervised statistical/machine learning (ML) methods are explicitly designed to solve prediction problems very well. Achieving this goal does not imply that these methods automatically deliver good estimators of causal parameters. Examples of such parameters include individual regression coefficients, average treatment effects, average lifts, and demand or supply elasticities. In fact, estimates of such causal parameters obtained via naively plugging ML estimators into estimating equations for such parameters can behave very poorly due to the regularization bias. Fortunately, this regularization bias can be removed by solving auxiliary prediction problems via ML tools. Specifically, we can form an orthogonal score for the target low-dimensional parameter by combining auxiliary and main ML predictions. The score is then used to build a de-biased estimator of the target parameter which typically will converge at the fastest possible 1/root(n) rate and be approximately unbiased and normal, and from which valid confidence intervals for these parameters of interest may be constructed. The resulting method thus could be called a "double ML" method because it relies on estimating primary and auxiliary predictive models. In order to avoid overfitting, our construction also makes use of the K-fold sample splitting, which we call cross-fitting. This allows us to use a very broad set of ML predictive methods in solving the auxiliary and main prediction problems, such as random forest, lasso, ridge, deep neural nets, boosted trees, as well as various hybrids and aggregators of these methods.

Double/Debiased/Neyman Machine Learning of Treatment Effects

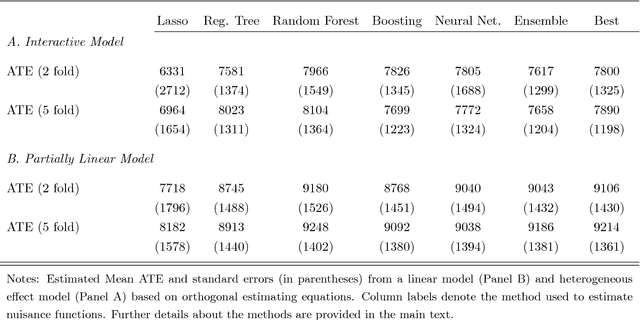
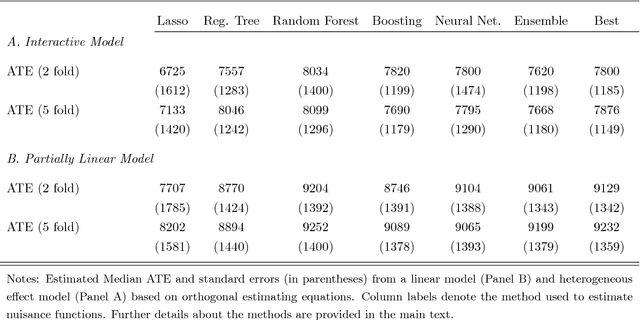
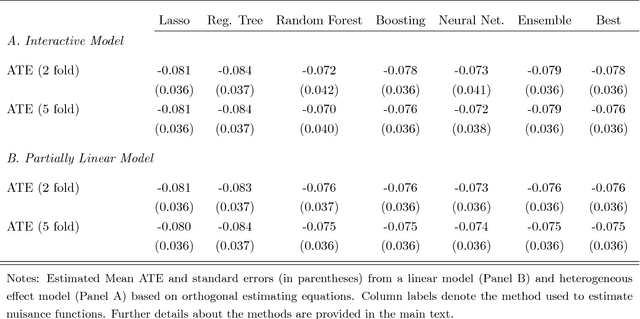
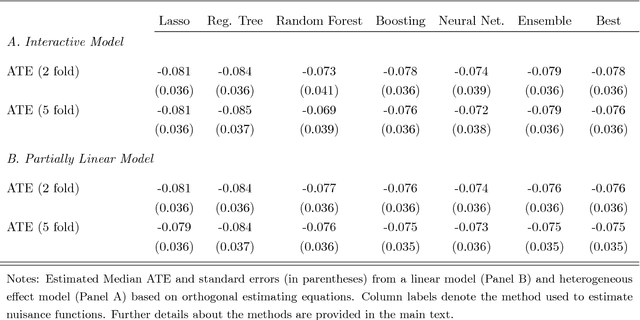
Chernozhukov, Chetverikov, Demirer, Duflo, Hansen, and Newey (2016) provide a generic double/de-biased machine learning (DML) approach for obtaining valid inferential statements about focal parameters, using Neyman-orthogonal scores and cross-fitting, in settings where nuisance parameters are estimated using a new generation of nonparametric fitting methods for high-dimensional data, called machine learning methods. In this note, we illustrate the application of this method in the context of estimating average treatment effects (ATE) and average treatment effects on the treated (ATTE) using observational data. A more general discussion and references to the existing literature are available in Chernozhukov, Chetverikov, Demirer, Duflo, Hansen, and Newey (2016).