Weighted-average quantile regression

In this paper, we introduce the weighted-average quantile regression framework, $\int_0^1 q_{Y|X}(u)\psi(u)du = X'\beta$, where $Y$ is a dependent variable, $X$ is a vector of covariates, $q_{Y|X}$ is the quantile function of the conditional distribution of $Y$ given $X$, $\psi$ is a weighting function, and $\beta$ is a vector of parameters. We argue that this framework is of interest in many applied settings and develop an estimator of the vector of parameters $\beta$. We show that our estimator is $\sqrt T$-consistent and asymptotically normal with mean zero and easily estimable covariance matrix, where $T$ is the size of available sample. We demonstrate the usefulness of our estimator by applying it in two empirical settings. In the first setting, we focus on financial data and study the factor structures of the expected shortfalls of the industry portfolios. In the second setting, we focus on wage data and study inequality and social welfare dependence on commonly used individual characteristics.

Double/Debiased Machine Learning for Treatment and Causal Parameters

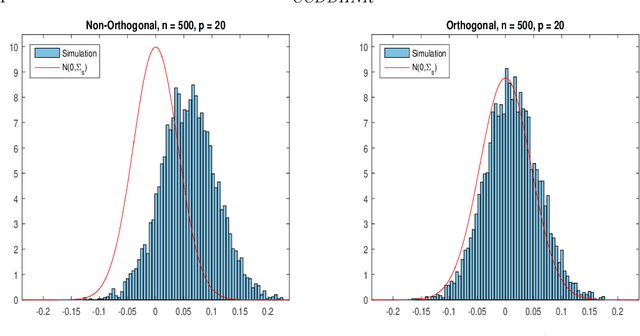
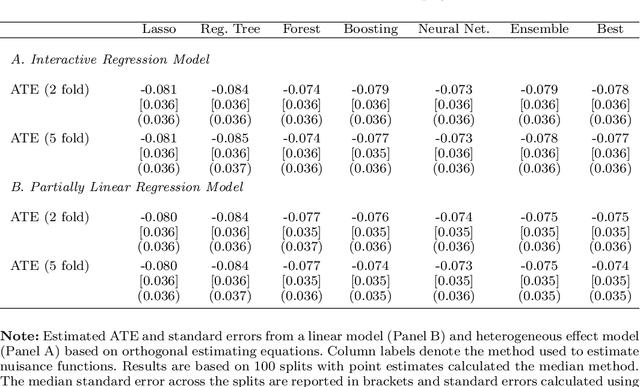
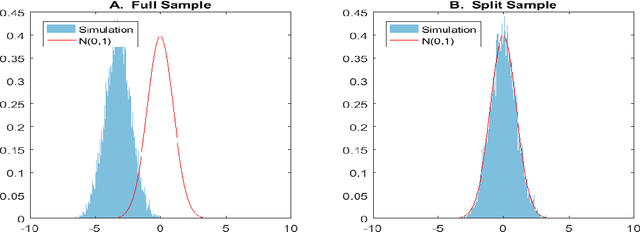
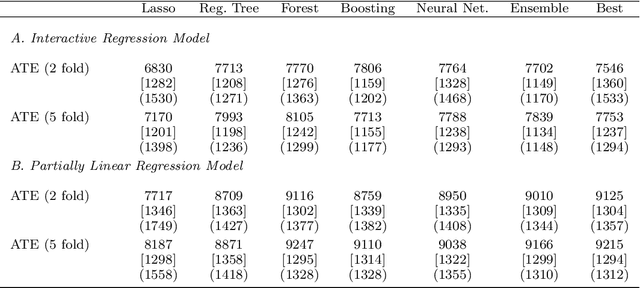
Most modern supervised statistical/machine learning (ML) methods are explicitly designed to solve prediction problems very well. Achieving this goal does not imply that these methods automatically deliver good estimators of causal parameters. Examples of such parameters include individual regression coefficients, average treatment effects, average lifts, and demand or supply elasticities. In fact, estimates of such causal parameters obtained via naively plugging ML estimators into estimating equations for such parameters can behave very poorly due to the regularization bias. Fortunately, this regularization bias can be removed by solving auxiliary prediction problems via ML tools. Specifically, we can form an orthogonal score for the target low-dimensional parameter by combining auxiliary and main ML predictions. The score is then used to build a de-biased estimator of the target parameter which typically will converge at the fastest possible 1/root(n) rate and be approximately unbiased and normal, and from which valid confidence intervals for these parameters of interest may be constructed. The resulting method thus could be called a "double ML" method because it relies on estimating primary and auxiliary predictive models. In order to avoid overfitting, our construction also makes use of the K-fold sample splitting, which we call cross-fitting. This allows us to use a very broad set of ML predictive methods in solving the auxiliary and main prediction problems, such as random forest, lasso, ridge, deep neural nets, boosted trees, as well as various hybrids and aggregators of these methods.

Double/Debiased/Neyman Machine Learning of Treatment Effects

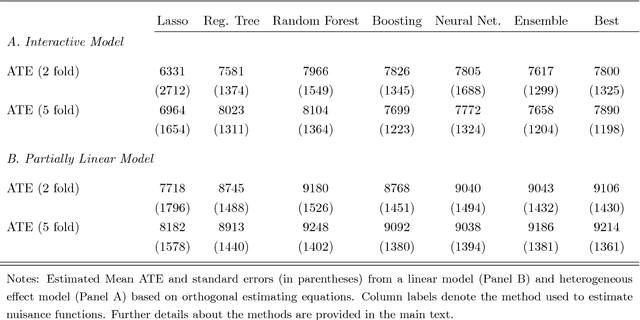
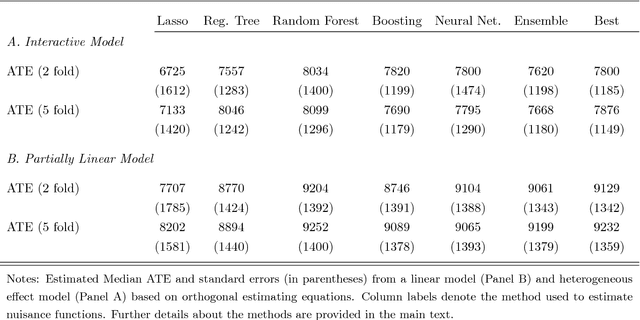
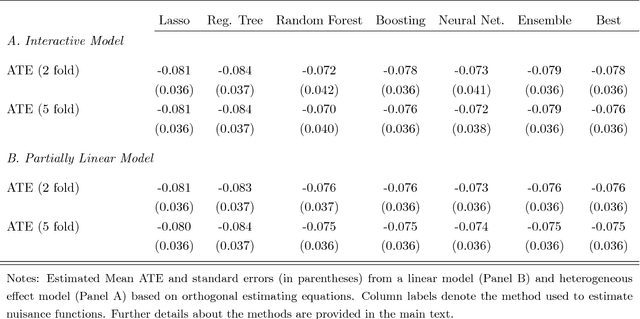
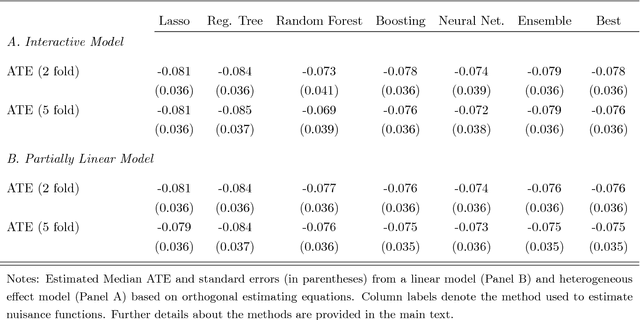
Chernozhukov, Chetverikov, Demirer, Duflo, Hansen, and Newey (2016) provide a generic double/de-biased machine learning (DML) approach for obtaining valid inferential statements about focal parameters, using Neyman-orthogonal scores and cross-fitting, in settings where nuisance parameters are estimated using a new generation of nonparametric fitting methods for high-dimensional data, called machine learning methods. In this note, we illustrate the application of this method in the context of estimating average treatment effects (ATE) and average treatment effects on the treated (ATTE) using observational data. A more general discussion and references to the existing literature are available in Chernozhukov, Chetverikov, Demirer, Duflo, Hansen, and Newey (2016).