TransformerLSR: Attentive Joint Model of Longitudinal Data, Survival, and Recurrent Events with Concurrent Latent Structure

In applications such as biomedical studies, epidemiology, and social sciences, recurrent events often co-occur with longitudinal measurements and a terminal event, such as death. Therefore, jointly modeling longitudinal measurements, recurrent events, and survival data while accounting for their dependencies is critical. While joint models for the three components exist in statistical literature, many of these approaches are limited by heavy parametric assumptions and scalability issues. Recently, incorporating deep learning techniques into joint modeling has shown promising results. However, current methods only address joint modeling of longitudinal measurements at regularly-spaced observation times and survival events, neglecting recurrent events. In this paper, we develop TransformerLSR, a flexible transformer-based deep modeling and inference framework to jointly model all three components simultaneously. TransformerLSR integrates deep temporal point processes into the joint modeling framework, treating recurrent and terminal events as two competing processes dependent on past longitudinal measurements and recurrent event times. Additionally, TransformerLSR introduces a novel trajectory representation and model architecture to potentially incorporate a priori knowledge of known latent structures among concurrent longitudinal variables. We demonstrate the effectiveness and necessity of TransformerLSR through simulation studies and analyzing a real-world medical dataset on patients after kidney transplantation.

MoMA: Model-based Mirror Ascent for Offline Reinforcement Learning

Model-based offline reinforcement learning methods (RL) have achieved state-of-the-art performance in many decision-making problems thanks to their sample efficiency and generalizability. Despite these advancements, existing model-based offline RL approaches either focus on theoretical studies without developing practical algorithms or rely on a restricted parametric policy space, thus not fully leveraging the advantages of an unrestricted policy space inherent to model-based methods. To address this limitation, we develop MoMA, a model-based mirror ascent algorithm with general function approximations under partial coverage of offline data. MoMA distinguishes itself from existing literature by employing an unrestricted policy class. In each iteration, MoMA conservatively estimates the value function by a minimization procedure within a confidence set of transition models in the policy evaluation step, then updates the policy with general function approximations instead of commonly-used parametric policy classes in the policy improvement step. Under some mild assumptions, we establish theoretical guarantees of MoMA by proving an upper bound on the suboptimality of the returned policy. We also provide a practically implementable, approximate version of the algorithm. The effectiveness of MoMA is demonstrated via numerical studies.

A Policy Gradient Method for Confounded POMDPs

In this paper, we propose a policy gradient method for confounded partially observable Markov decision processes (POMDPs) with continuous state and observation spaces in the offline setting. We first establish a novel identification result to non-parametrically estimate any history-dependent policy gradient under POMDPs using the offline data. The identification enables us to solve a sequence of conditional moment restrictions and adopt the min-max learning procedure with general function approximation for estimating the policy gradient. We then provide a finite-sample non-asymptotic bound for estimating the gradient uniformly over a pre-specified policy class in terms of the sample size, length of horizon, concentratability coefficient and the measure of ill-posedness in solving the conditional moment restrictions. Lastly, by deploying the proposed gradient estimation in the gradient ascent algorithm, we show the global convergence of the proposed algorithm in finding the history-dependent optimal policy under some technical conditions. To the best of our knowledge, this is the first work studying the policy gradient method for POMDPs under the offline setting.

Offline Reinforcement Learning with Instrumental Variables in Confounded Markov Decision Processes

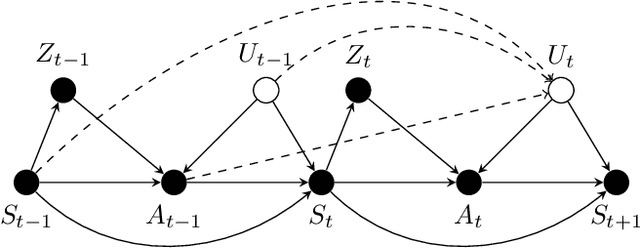
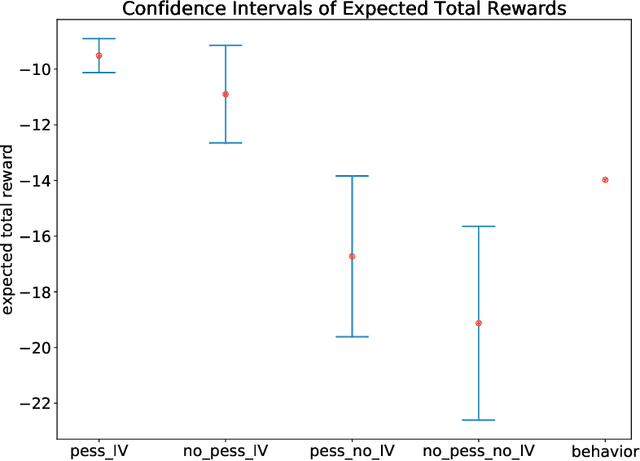
We study the offline reinforcement learning (RL) in the face of unmeasured confounders. Due to the lack of online interaction with the environment, offline RL is facing the following two significant challenges: (i) the agent may be confounded by the unobserved state variables; (ii) the offline data collected a prior does not provide sufficient coverage for the environment. To tackle the above challenges, we study the policy learning in the confounded MDPs with the aid of instrumental variables. Specifically, we first establish value function (VF)-based and marginalized importance sampling (MIS)-based identification results for the expected total reward in the confounded MDPs. Then by leveraging pessimism and our identification results, we propose various policy learning methods with the finite-sample suboptimality guarantee of finding the optimal in-class policy under minimal data coverage and modeling assumptions. Lastly, our extensive theoretical investigations and one numerical study motivated by the kidney transplantation demonstrate the promising performance of the proposed methods.

Data-driven discovery of interpretable causal relations for deep learning material laws with uncertainty propagation

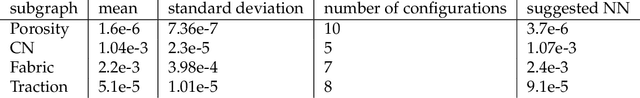
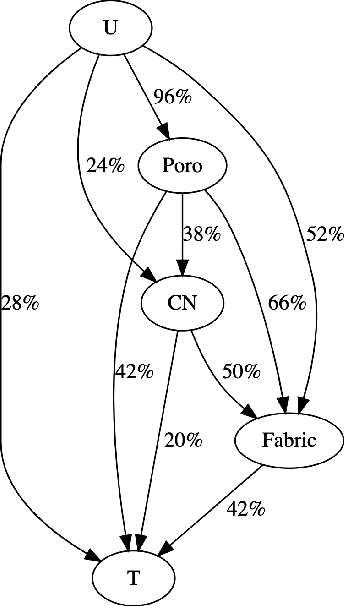
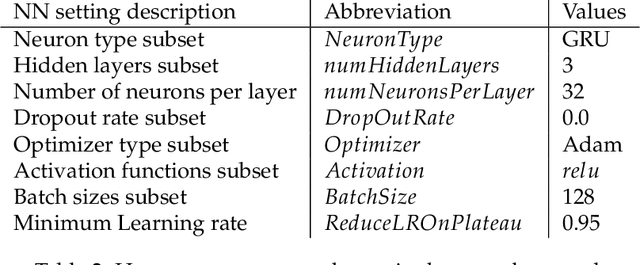
This paper presents a computational framework that generates ensemble predictive mechanics models with uncertainty quantification (UQ). We first develop a causal discovery algorithm to infer causal relations among time-history data measured during each representative volume element (RVE) simulation through a directed acyclic graph (DAG). With multiple plausible sets of causal relationships estimated from multiple RVE simulations, the predictions are propagated in the derived causal graph while using a deep neural network equipped with dropout layers as a Bayesian approximation for uncertainty quantification. We select two representative numerical examples (traction-separation laws for frictional interfaces, elastoplasticity models for granular assembles) to examine the accuracy and robustness of the proposed causal discovery method for the common material law predictions in civil engineering applications.

A Bayesian Nonparametric Approach for Estimating Individualized Treatment-Response Curves

We study the problem of estimating the continuous response over time to interventions using observational time series---a retrospective dataset where the policy by which the data are generated is unknown to the learner. We are motivated by applications where response varies by individuals and therefore, estimating responses at the individual-level is valuable for personalizing decision-making. We refer to this as the problem of estimating individualized treatment response (ITR) curves. In statistics, G-computation formula (Robins, 1986) has been commonly used for estimating treatment responses from observational data containing sequential treatment assignments. However, past studies have focused predominantly on obtaining point-in-time estimates at the population level. We leverage the G-computation formula and develop a novel Bayesian nonparametric (BNP) method that can flexibly model functional data and provide posterior inference over the treatment response curves at both the individual and population level. On a challenging dataset containing time series from patients admitted to a hospital, we estimate responses to treatments used in managing kidney function and show that the resulting fits are more accurate than alternative approaches. Accurate methods for obtaining ITRs from observational data can dramatically accelerate the pace at which personalized treatment plans become possible.