Offline Reinforcement Learning for Human-Guided Human-Machine Interaction with Private Information

Motivated by the human-machine interaction such as training chatbots for improving customer satisfaction, we study human-guided human-machine interaction involving private information. We model this interaction as a two-player turn-based game, where one player (Alice, a human) guides the other player (Bob, a machine) towards a common goal. Specifically, we focus on offline reinforcement learning (RL) in this game, where the goal is to find a policy pair for Alice and Bob that maximizes their expected total rewards based on an offline dataset collected a priori. The offline setting presents two challenges: (i) We cannot collect Bob's private information, leading to a confounding bias when using standard RL methods, and (ii) a distributional mismatch between the behavior policy used to collect data and the desired policy we aim to learn. To tackle the confounding bias, we treat Bob's previous action as an instrumental variable for Alice's current decision making so as to adjust for the unmeasured confounding. We develop a novel identification result and use it to propose a new off-policy evaluation (OPE) method for evaluating policy pairs in this two-player turn-based game. To tackle the distributional mismatch, we leverage the idea of pessimism and use our OPE method to develop an off-policy learning algorithm for finding a desirable policy pair for both Alice and Bob. Finally, we prove that under mild assumptions such as partial coverage of the offline data, the policy pair obtained through our method converges to the optimal one at a satisfactory rate.

Offline Reinforcement Learning with Instrumental Variables in Confounded Markov Decision Processes

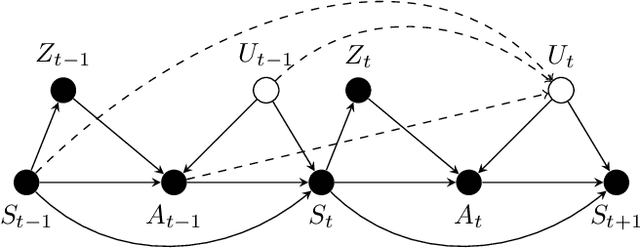
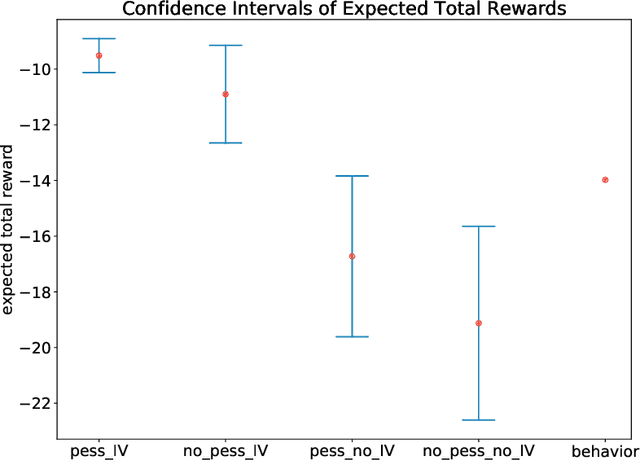
We study the offline reinforcement learning (RL) in the face of unmeasured confounders. Due to the lack of online interaction with the environment, offline RL is facing the following two significant challenges: (i) the agent may be confounded by the unobserved state variables; (ii) the offline data collected a prior does not provide sufficient coverage for the environment. To tackle the above challenges, we study the policy learning in the confounded MDPs with the aid of instrumental variables. Specifically, we first establish value function (VF)-based and marginalized importance sampling (MIS)-based identification results for the expected total reward in the confounded MDPs. Then by leveraging pessimism and our identification results, we propose various policy learning methods with the finite-sample suboptimality guarantee of finding the optimal in-class policy under minimal data coverage and modeling assumptions. Lastly, our extensive theoretical investigations and one numerical study motivated by the kidney transplantation demonstrate the promising performance of the proposed methods.

SCORE: Spurious COrrelation REduction for Offline Reinforcement Learning

Offline reinforcement learning (RL) aims to learn the optimal policy from a pre-collected dataset without online interactions. Most of the existing studies focus on distributional shift caused by out-of-distribution actions. However, even in-distribution actions can raise serious problems. Since the dataset only contains limited information about the underlying model, offline RL is vulnerable to spurious correlations, i.e., the agent tends to prefer actions that by chance lead to high returns, resulting in a highly suboptimal policy. To address such a challenge, we propose a practical and theoretically guaranteed algorithm SCORE that reduces spurious correlations by combing an uncertainty penalty into policy evaluation. We show that this is consistent with the pessimism principle studied in theory, and the proposed algorithm converges to the optimal policy with a sublinear rate under mild assumptions. By conducting extensive experiments on existing benchmarks, we show that SCORE not only benefits from a solid theory but also obtains strong empirical results on a variety of tasks.

Provably Efficient Generative Adversarial Imitation Learning for Online and Offline Setting with Linear Function Approximation

In generative adversarial imitation learning (GAIL), the agent aims to learn a policy from an expert demonstration so that its performance cannot be discriminated from the expert policy on a certain predefined reward set. In this paper, we study GAIL in both online and offline settings with linear function approximation, where both the transition and reward function are linear in the feature maps. Besides the expert demonstration, in the online setting the agent can interact with the environment, while in the offline setting the agent only accesses an additional dataset collected by a prior. For online GAIL, we propose an optimistic generative adversarial policy optimization algorithm (OGAP) and prove that OGAP achieves $\widetilde{\mathcal{O}}(H^2 d^{3/2}K^{1/2}+KH^{3/2}dN_1^{-1/2})$ regret. Here $N_1$ represents the number of trajectories of the expert demonstration, $d$ is the feature dimension, and $K$ is the number of episodes. For offline GAIL, we propose a pessimistic generative adversarial policy optimization algorithm (PGAP). For an arbitrary additional dataset, we obtain the optimality gap of PGAP, achieving the minimax lower bound in the utilization of the additional dataset. Assuming sufficient coverage on the additional dataset, we show that PGAP achieves $\widetilde{\mathcal{O}}(H^{2}dK^{-1/2} +H^2d^{3/2}N_2^{-1/2}+H^{3/2}dN_1^{-1/2} \ )$ optimality gap. Here $N_2$ represents the number of trajectories of the additional dataset with sufficient coverage.

Instrumental Variable Value Iteration for Causal Offline Reinforcement Learning

In offline reinforcement learning (RL) an optimal policy is learnt solely from a priori collected observational data. However, in observational data, actions are often confounded by unobserved variables. Instrumental variables (IVs), in the context of RL, are the variables whose influence on the state variables are all mediated through the action. When a valid instrument is present, we can recover the confounded transition dynamics through observational data. We study a confounded Markov decision process where the transition dynamics admit an additive nonlinear functional form. Using IVs, we derive a conditional moment restriction (CMR) through which we can identify transition dynamics based on observational data. We propose a provably efficient IV-aided Value Iteration (IVVI) algorithm based on a primal-dual reformulation of CMR. To the best of our knowledge, this is the first provably efficient algorithm for instrument-aided offline RL.

Single-Timescale Actor-Critic Provably Finds Globally Optimal Policy

We study the global convergence and global optimality of actor-critic, one of the most popular families of reinforcement learning algorithms. While most existing works on actor-critic employ bi-level or two-timescale updates, we focus on the more practical single-timescale setting, where the actor and critic are updated simultaneously. Specifically, in each iteration, the critic update is obtained by applying the Bellman evaluation operator only once while the actor is updated in the policy gradient direction computed using the critic. Moreover, we consider two function approximation settings where both the actor and critic are represented by linear or deep neural networks. For both cases, we prove that the actor sequence converges to a globally optimal policy at a sublinear $O(K^{-1/2})$ rate, where $K$ is the number of iterations. To the best of our knowledge, we establish the rate of convergence and global optimality of single-timescale actor-critic with linear function approximation for the first time. Moreover, under the broader scope of policy optimization with nonlinear function approximation, we prove that actor-critic with deep neural network finds the globally optimal policy at a sublinear rate for the first time.

Actor-Critic Provably Finds Nash Equilibria of Linear-Quadratic Mean-Field Games

We study discrete-time mean-field Markov games with infinite numbers of agents where each agent aims to minimize its ergodic cost. We consider the setting where the agents have identical linear state transitions and quadratic cost functions, while the aggregated effect of the agents is captured by the population mean of their states, namely, the mean-field state. For such a game, based on the Nash certainty equivalence principle, we provide sufficient conditions for the existence and uniqueness of its Nash equilibrium. Moreover, to find the Nash equilibrium, we propose a mean-field actor-critic algorithm with linear function approximation, which does not require knowing the model of dynamics. Specifically, at each iteration of our algorithm, we use the single-agent actor-critic algorithm to approximately obtain the optimal policy of the each agent given the current mean-field state, and then update the mean-field state. In particular, we prove that our algorithm converges to the Nash equilibrium at a linear rate. To the best of our knowledge, this is the first success of applying model-free reinforcement learning with function approximation to discrete-time mean-field Markov games with provable non-asymptotic global convergence guarantees.

Credible Sample Elicitation by Deep Learning, for Deep Learning

It is important to collect credible training samples $(x,y)$ for building data-intensive learning systems (e.g., a deep learning system). In the literature, there is a line of studies on eliciting distributional information from self-interested agents who hold a relevant information. Asking people to report complex distribution $p(x)$, though theoretically viable, is challenging in practice. This is primarily due to the heavy cognitive loads required for human agents to reason and report this high dimensional information. Consider the example where we are interested in building an image classifier via first collecting a certain category of high-dimensional image data. While classical elicitation results apply to eliciting a complex and generative (and continuous) distribution $p(x)$ for this image data, we are interested in eliciting samples $x_i \sim p(x)$ from agents. This paper introduces a deep learning aided method to incentivize credible sample contributions from selfish and rational agents. The challenge to do so is to design an incentive-compatible score function to score each reported sample to induce truthful reports, instead of an arbitrary or even adversarial one. We show that with accurate estimation of a certain $f$-divergence function we are able to achieve approximate incentive compatibility in eliciting truthful samples. We then present an efficient estimator with theoretical guarantee via studying the variational forms of $f$-divergence function. Our work complements the literature of information elicitation via introducing the problem of \emph{sample elicitation}. We also show a connection between this sample elicitation problem and $f$-GAN, and how this connection can help reconstruct an estimator of the distribution based on collected samples.