Distributional Random Forests for Complex Survey Designs on Reproducing Kernel Hilbert Spaces

We study estimation of the conditional law $P(Y|X=\mathbf{x})$ and continuous functionals $Ψ(P(Y|X=\mathbf{x}))$ when $Y$ takes values in a locally compact Polish space, $X \in \mathbb{R}^p$, and the observations arise from a complex survey design. We propose a survey-calibrated distributional random forest (SDRF) that incorporates complex-design features via a pseudo-population bootstrap, PSU-level honesty, and a Maximum Mean Discrepancy (MMD) split criterion computed from kernel mean embeddings of Hájek-type (design-weighted) node distributions. We provide a framework for analyzing forest-style estimators under survey designs; establish design consistency for the finite-population target and model consistency for the super-population target under explicit conditions on the design, kernel, resampling multipliers, and tree partitions. As far as we are aware, these are the first results on model-free estimation of conditional distributions under survey designs. Simulations under a stratified two-stage cluster design provide finite sample performance and demonstrate the statistical error price of ignoring the survey design. The broad applicability of SDRF is demonstrated using NHANES: We estimate the tolerance regions of the conditional joint distribution of two diabetes biomarkers, illustrating how distributional heterogeneity can support subgroup-specific risk profiling for diabetes mellitus in the U.S. population.

Off-Policy Reinforcement Learning with High Dimensional Reward

Conventional off-policy reinforcement learning (RL) focuses on maximizing the expected return of scalar rewards. Distributional RL (DRL), in contrast, studies the distribution of returns with the distributional Bellman operator in a Euclidean space, leading to highly flexible choices for utility. This paper establishes robust theoretical foundations for DRL. We prove the contraction property of the Bellman operator even when the reward space is an infinite-dimensional separable Banach space. Furthermore, we demonstrate that the behavior of high- or infinite-dimensional returns can be effectively approximated using a lower-dimensional Euclidean space. Leveraging these theoretical insights, we propose a novel DRL algorithm that tackles problems which have been previously intractable using conventional reinforcement learning approaches.

Medical Knowledge Integration into Reinforcement Learning Algorithms for Dynamic Treatment Regimes

The goal of precision medicine is to provide individualized treatment at each stage of chronic diseases, a concept formalized by Dynamic Treatment Regimes (DTR). These regimes adapt treatment strategies based on decision rules learned from clinical data to enhance therapeutic effectiveness. Reinforcement Learning (RL) algorithms allow to determine these decision rules conditioned by individual patient data and their medical history. The integration of medical expertise into these models makes possible to increase confidence in treatment recommendations and facilitate the adoption of this approach by healthcare professionals and patients. In this work, we examine the mathematical foundations of RL, contextualize its application in the field of DTR, and present an overview of methods to improve its effectiveness by integrating medical expertise.

A Flexible Framework for Incorporating Patient Preferences Into Q-Learning

In real-world healthcare problems, there are often multiple competing outcomes of interest, such as treatment efficacy and side effect severity. However, statistical methods for estimating dynamic treatment regimes (DTRs) usually assume a single outcome of interest, and the few methods that deal with composite outcomes suffer from important limitations. This includes restrictions to a single time point and two outcomes, the inability to incorporate self-reported patient preferences and limited theoretical guarantees. To this end, we propose a new method to address these limitations, which we dub Latent Utility Q-Learning (LUQ-Learning). LUQ-Learning uses a latent model approach to naturally extend Q-learning to the composite outcome setting and adopt the ideal trade-off between outcomes to each patient. Unlike previous approaches, our framework allows for an arbitrary number of time points and outcomes, incorporates stated preferences and achieves strong asymptotic performance with realistic assumptions on the data. We conduct simulation experiments based on an ongoing trial for low back pain as well as a well-known completed trial for schizophrenia. In all experiments, our method achieves highly competitive empirical performance compared to several alternative baselines.

Revisiting Bellman Errors for Offline Model Selection

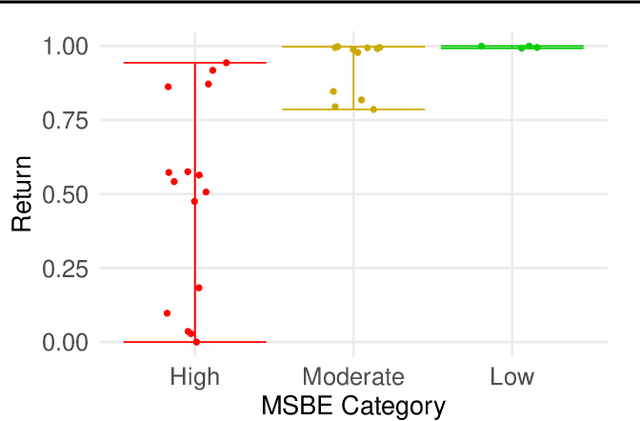
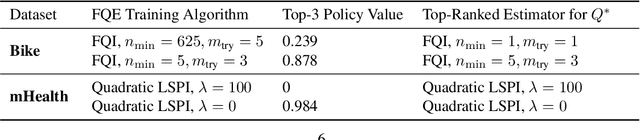
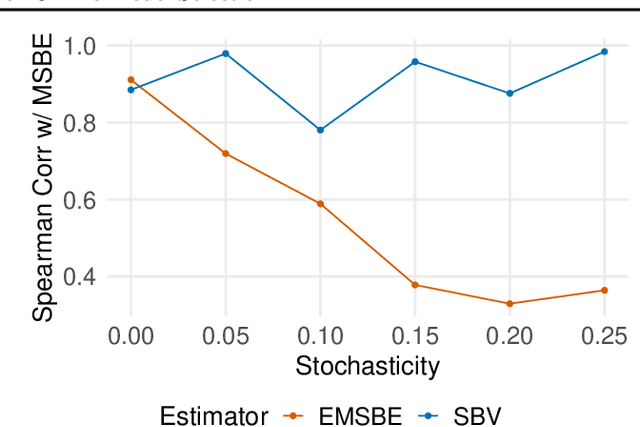
Offline model selection (OMS), that is, choosing the best policy from a set of many policies given only logged data, is crucial for applying offline RL in real-world settings. One idea that has been extensively explored is to select policies based on the mean squared Bellman error (MSBE) of the associated Q-functions. However, previous work has struggled to obtain adequate OMS performance with Bellman errors, leading many researchers to abandon the idea. Through theoretical and empirical analyses, we elucidate why previous work has seen pessimistic results with Bellman errors and identify conditions under which OMS algorithms based on Bellman errors will perform well. Moreover, we develop a new estimator of the MSBE that is more accurate than prior methods and obtains impressive OMS performance on diverse discrete control tasks, including Atari games. We open-source our data and code to enable researchers to conduct OMS experiments more easily.

Offline Reinforcement Learning with Instrumental Variables in Confounded Markov Decision Processes

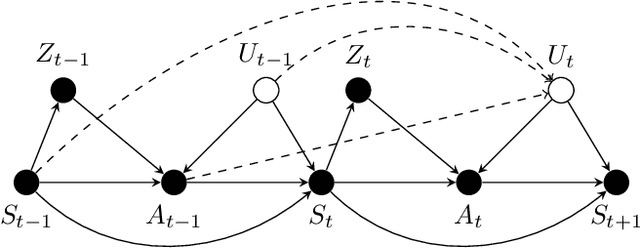
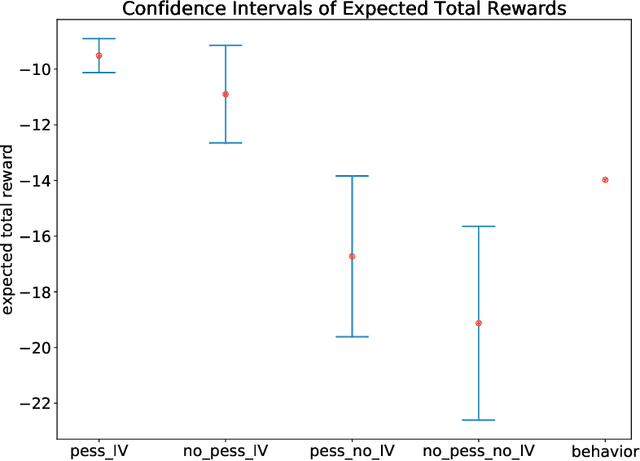
We study the offline reinforcement learning (RL) in the face of unmeasured confounders. Due to the lack of online interaction with the environment, offline RL is facing the following two significant challenges: (i) the agent may be confounded by the unobserved state variables; (ii) the offline data collected a prior does not provide sufficient coverage for the environment. To tackle the above challenges, we study the policy learning in the confounded MDPs with the aid of instrumental variables. Specifically, we first establish value function (VF)-based and marginalized importance sampling (MIS)-based identification results for the expected total reward in the confounded MDPs. Then by leveraging pessimism and our identification results, we propose various policy learning methods with the finite-sample suboptimality guarantee of finding the optimal in-class policy under minimal data coverage and modeling assumptions. Lastly, our extensive theoretical investigations and one numerical study motivated by the kidney transplantation demonstrate the promising performance of the proposed methods.

Neural interval-censored Cox regression with feature selection

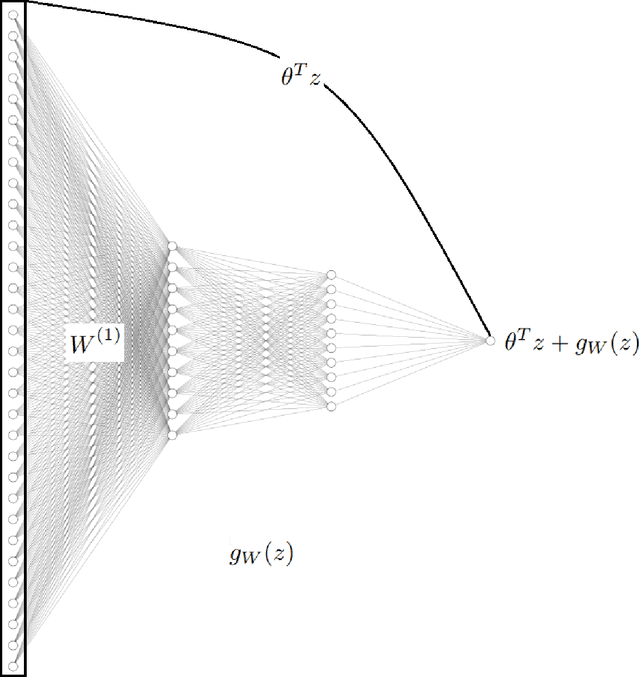
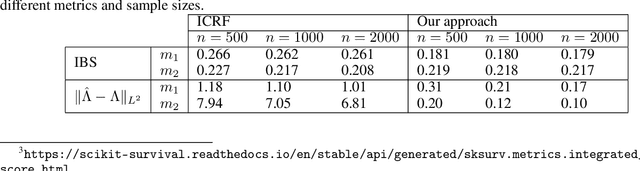
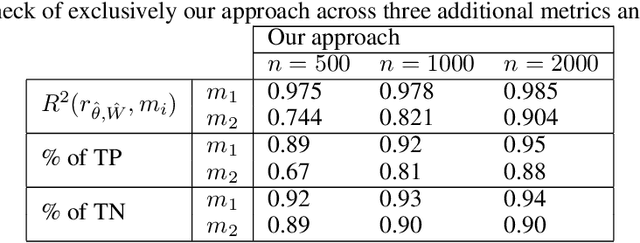
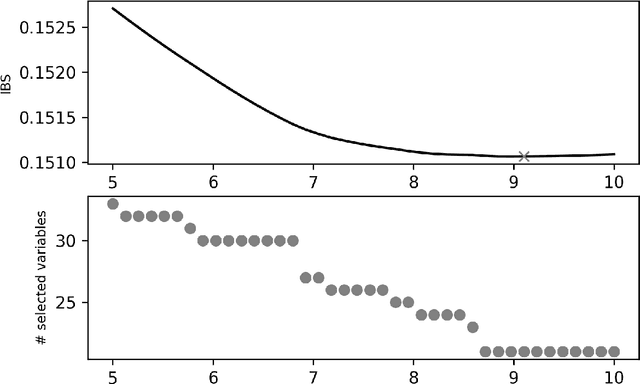
The classical Cox model emerged in 1972 promoting breakthroughs in how patient prognosis is quantified using time-to-event analysis in biomedicine. One of the most useful characteristics of the model for practitioners is the interpretability of the variables in the analysis. However, this comes at the price of introducing strong assumptions concerning the functional form of the regression model. To break this gap, this paper aims to exploit the explainability advantages of the classical Cox model in the setting of interval-censoring using a new Lasso neural network that simultaneously selects the most relevant variables while quantifying non-linear relations between predictors and survival times. The gain of the new method is illustrated empirically in an extensive simulation study with examples that involve linear and non-linear ground dependencies. We also demonstrate the performance of our strategy in the analysis of physiological, clinical and accelerometer data from the NHANES 2003-2006 waves to predict the effect of physical activity on the survival of patients. Our method outperforms the prior results in the literature that use the traditional Cox model.

Discussion of Multiscale Fisher's Independence Test for Multivariate Dependence

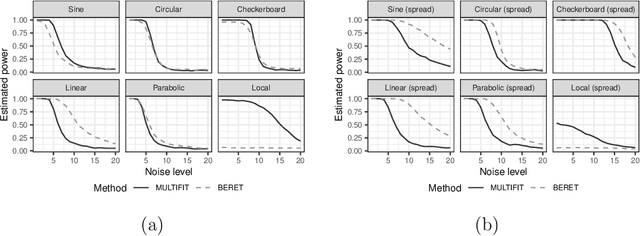
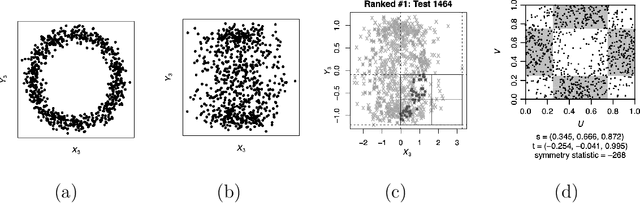
The multiscale Fisher's independence test (MULTIFIT hereafter) proposed by Gorsky & Ma (2022) is a novel method to test independence between two random vectors. By its design, this test is particularly useful in detecting local dependence. Moreover, by adopting a resampling-free approach, it can easily accommodate massive sample sizes. Another benefit of the proposed method is its ability to interpret the nature of dependency. We congratulate the authors, Shai Gorksy and Li Ma, for their very interesting and elegant work. In this comment, we would like to discuss a general framework unifying the MULTIFIT and other tests and compare it with the binary expansion randomized ensemble test (BERET hereafter) proposed by Lee et al. (In press). We also would like to contribute our thoughts on potential extensions of the method.

Kernel Assisted Learning for Personalized Dose Finding

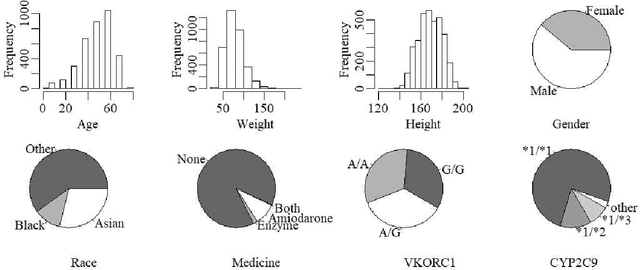
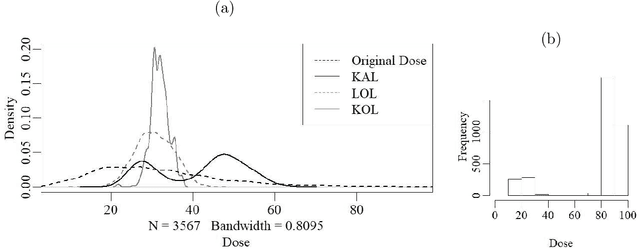
An individualized dose rule recommends a dose level within a continuous safe dose range based on patient level information such as physical conditions, genetic factors and medication histories. Traditionally, personalized dose finding process requires repeating clinical visits of the patient and frequent adjustments of the dosage. Thus the patient is constantly exposed to the risk of underdosing and overdosing during the process. Statistical methods for finding an optimal individualized dose rule can lower the costs and risks for patients. In this article, we propose a kernel assisted learning method for estimating the optimal individualized dose rule. The proposed methodology can also be applied to all other continuous decision-making problems. Advantages of the proposed method include robustness to model misspecification and capability of providing statistical inference for the estimated parameters. In the simulation studies, we show that this method is capable of identifying the optimal individualized dose rule and produces favorable expected outcomes in the population. Finally, we illustrate our approach using data from a warfarin dosing study for thrombosis patients.

Missing Data Imputation for Classification Problems

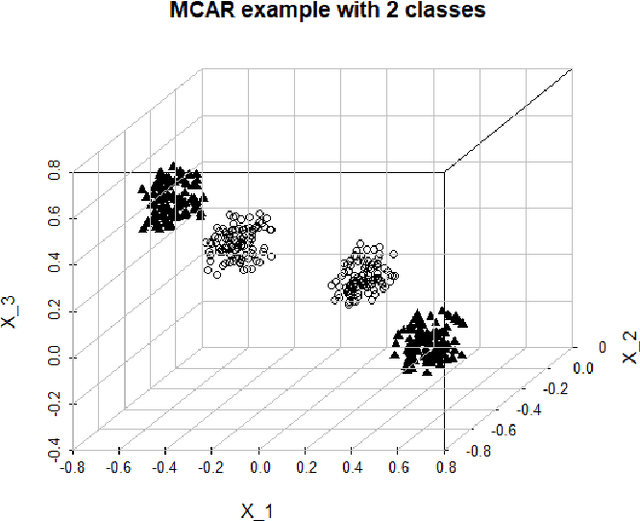
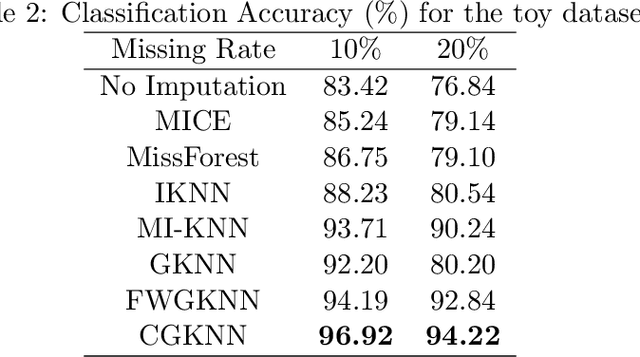
Imputation of missing data is a common application in various classification problems where the feature training matrix has missingness. A widely used solution to this imputation problem is based on the lazy learning technique, $k$-nearest neighbor (kNN) approach. However, most of the previous work on missing data does not take into account the presence of the class label in the classification problem. Also, existing kNN imputation methods use variants of Minkowski distance as a measure of distance, which does not work well with heterogeneous data. In this paper, we propose a novel iterative kNN imputation technique based on class weighted grey distance between the missing datum and all the training data. Grey distance works well in heterogeneous data with missing instances. The distance is weighted by Mutual Information (MI) which is a measure of feature relevance between the features and the class label. This ensures that the imputation of the training data is directed towards improving classification performance. This class weighted grey kNN imputation algorithm demonstrates improved performance when compared to other kNN imputation algorithms, as well as standard imputation algorithms such as MICE and missForest, in imputation and classification problems. These problems are based on simulated scenarios and UCI datasets with various rates of missingness.