Model-Free Kernel Conformal Depth Measures Algorithm for Uncertainty Quantification in Regression Models in Separable Hilbert Spaces

Depth measures are powerful tools for defining level sets in emerging, non--standard, and complex random objects such as high-dimensional multivariate data, functional data, and random graphs. Despite their favorable theoretical properties, the integration of depth measures into regression modeling to provide prediction regions remains a largely underexplored area of research. To address this gap, we propose a novel, model-free uncertainty quantification algorithm based on conditional depth measures--specifically, conditional kernel mean embeddings and an integrated depth measure. These new algorithms can be used to define prediction and tolerance regions when predictors and responses are defined in separable Hilbert spaces. The use of kernel mean embeddings ensures faster convergence rates in prediction region estimation. To enhance the practical utility of the algorithms with finite samples, we also introduce a conformal prediction variant that provides marginal, non-asymptotic guarantees for the derived prediction regions. Additionally, we establish both conditional and unconditional consistency results, as well as fast convergence rates in certain homoscedastic settings. We evaluate the finite--sample performance of our model in extensive simulation studies involving various types of functional data and traditional Euclidean scenarios. Finally, we demonstrate the practical relevance of our approach through a digital health application related to physical activity, aiming to provide personalized recommendations

Continuous Temporal Learning of Probability Distributions via Neural ODEs with Applications in Continuous Glucose Monitoring Data

Modeling the continuous--time dynamics of probability distributions from time--dependent data samples is a fundamental problem in many fields, including digital health. The aim is to analyze how the distribution of a biomarker, such as glucose, evolves over time and how these changes may reflect the progression of chronic diseases such as diabetes. In this paper, we propose a novel probabilistic model based on a mixture of Gaussian distributions to capture how samples from a continuous-time stochastic process evolve over the time. To model potential distribution shifts over time, we introduce a time-dependent function parameterized by a Neural Ordinary Differential Equation (Neural ODE) and estimate it non--parametrically using the Maximum Mean Discrepancy (MMD). The proposed model is highly interpretable, detects subtle temporal shifts, and remains computationally efficient. Through simulation studies, we show that it performs competitively in terms of estimation accuracy against state-of-the-art, less interpretable methods such as normalized gradient--flows and non--parameteric kernel density estimators. Finally, we demonstrate the utility of our method on digital clinical--trial data, showing how the interventions alters the time-dependent distribution of glucose levels and enabling a rigorous comparison of control and treatment groups from novel mathematical and clinical perspectives.

Variable Selection Methods for Multivariate, Functional, and Complex Biomedical Data in the AI Age

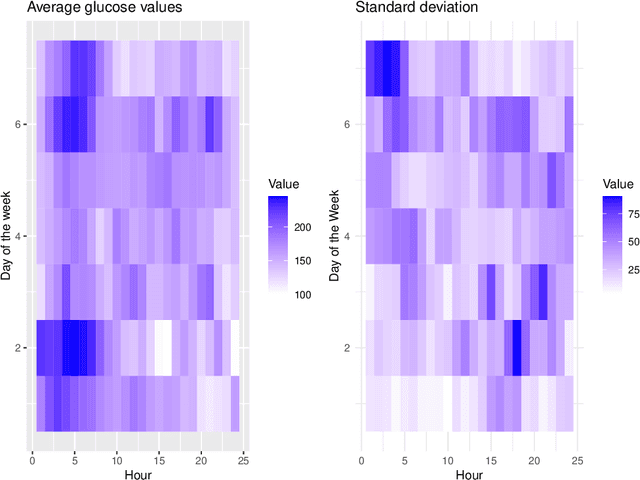
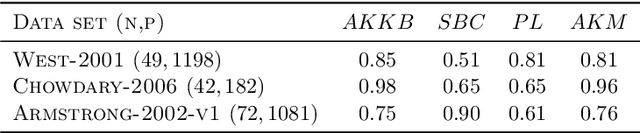
Many problems within personalized medicine and digital health rely on the analysis of continuous-time functional biomarkers and other complex data structures emerging from high-resolution patient monitoring. In this context, this work proposes new optimization-based variable selection methods for multivariate, functional, and even more general outcomes in metrics spaces based on best-subset selection. Our framework applies to several types of regression models, including linear, quantile, or non parametric additive models, and to a broad range of random responses, such as univariate, multivariate Euclidean data, functional, and even random graphs. Our analysis demonstrates that our proposed methodology outperforms state-of-the-art methods in accuracy and, especially, in speed-achieving several orders of magnitude improvement over competitors across various type of statistical responses as the case of mathematical functions. While our framework is general and is not designed for a specific regression and scientific problem, the article is self-contained and focuses on biomedical applications. In the clinical areas, serves as a valuable resource for professionals in biostatistics, statistics, and artificial intelligence interested in variable selection problem in this new technological AI-era.

Conformal Prediction in Dynamic Biological Systems

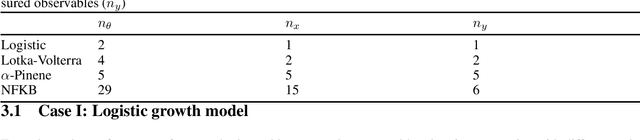
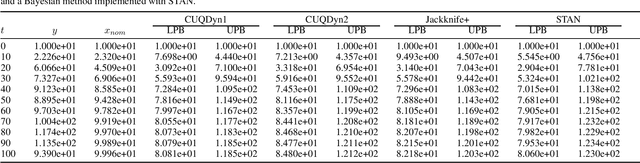
Uncertainty quantification (UQ) is the process of systematically determining and characterizing the degree of confidence in computational model predictions. In the context of systems biology, especially with dynamic models, UQ is crucial because it addresses the challenges posed by nonlinearity and parameter sensitivity, allowing us to properly understand and extrapolate the behavior of complex biological systems. Here, we focus on dynamic models represented by deterministic nonlinear ordinary differential equations. Many current UQ approaches in this field rely on Bayesian statistical methods. While powerful, these methods often require strong prior specifications and make parametric assumptions that may not always hold in biological systems. Additionally, these methods face challenges in domains where sample sizes are limited, and statistical inference becomes constrained, with computational speed being a bottleneck in large models of biological systems. As an alternative, we propose the use of conformal inference methods, introducing two novel algorithms that, in some instances, offer non-asymptotic guarantees, enhancing robustness and scalability across various applications. We demonstrate the efficacy of our proposed algorithms through several scenarios, highlighting their advantages over traditional Bayesian approaches. The proposed methods show promising results for diverse biological data structures and scenarios, offering a general framework to quantify uncertainty for dynamic models of biological systems.The software for the methodology and the reproduction of the results is available at https://zenodo.org/doi/10.5281/zenodo.13644870.

Uncertainty quantification in metric spaces

This paper introduces a novel uncertainty quantification framework for regression models where the response takes values in a separable metric space, and the predictors are in a Euclidean space. The proposed algorithms can efficiently handle large datasets and are agnostic to the predictive base model used. Furthermore, the algorithms possess asymptotic consistency guarantees and, in some special homoscedastic cases, we provide non-asymptotic guarantees. To illustrate the effectiveness of the proposed uncertainty quantification framework, we use a linear regression model for metric responses (known as the global Fr\'echet model) in various clinical applications related to precision and digital medicine. The different clinical outcomes analyzed are represented as complex statistical objects, including multivariate Euclidean data, Laplacian graphs, and probability distributions.

Deep Learning Framework with Uncertainty Quantification for Survey Data: Assessing and Predicting Diabetes Mellitus Risk in the American Population

Complex survey designs are commonly employed in many medical cohorts. In such scenarios, developing case-specific predictive risk score models that reflect the unique characteristics of the study design is essential. This approach is key to minimizing potential selective biases in results. The objectives of this paper are: (i) To propose a general predictive framework for regression and classification using neural network (NN) modeling, which incorporates survey weights into the estimation process; (ii) To introduce an uncertainty quantification algorithm for model prediction, tailored for data from complex survey designs; (iii) To apply this method in developing robust risk score models to assess the risk of Diabetes Mellitus in the US population, utilizing data from the NHANES 2011-2014 cohort. The theoretical properties of our estimators are designed to ensure minimal bias and the statistical consistency, thereby ensuring that our models yield reliable predictions and contribute novel scientific insights in diabetes research. While focused on diabetes, this NN predictive framework is adaptable to create clinical models for a diverse range of diseases and medical cohorts. The software and the data used in this paper is publicly available on GitHub.

kNN Algorithm for Conditional Mean and Variance Estimation with Automated Uncertainty Quantification and Variable Selection

In this paper, we introduce a kNN-based regression method that synergizes the scalability and adaptability of traditional non-parametric kNN models with a novel variable selection technique. This method focuses on accurately estimating the conditional mean and variance of random response variables, thereby effectively characterizing conditional distributions across diverse scenarios.Our approach incorporates a robust uncertainty quantification mechanism, leveraging our prior estimation work on conditional mean and variance. The employment of kNN ensures scalable computational efficiency in predicting intervals and statistical accuracy in line with optimal non-parametric rates. Additionally, we introduce a new kNN semi-parametric algorithm for estimating ROC curves, accounting for covariates. For selecting the smoothing parameter k, we propose an algorithm with theoretical guarantees.Incorporation of variable selection enhances the performance of the method significantly over conventional kNN techniques in various modeling tasks. We validate the approach through simulations in low, moderate, and high-dimensional covariate spaces. The algorithm's effectiveness is particularly notable in biomedical applications as demonstrated in two case studies. Concluding with a theoretical analysis, we highlight the consistency and convergence rate of our method over traditional kNN models, particularly when the underlying regression model takes values in a low-dimensional space.

Kernel Biclustering algorithm in Hilbert Spaces

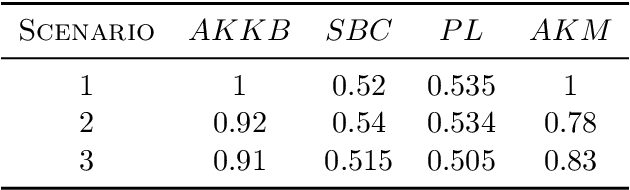
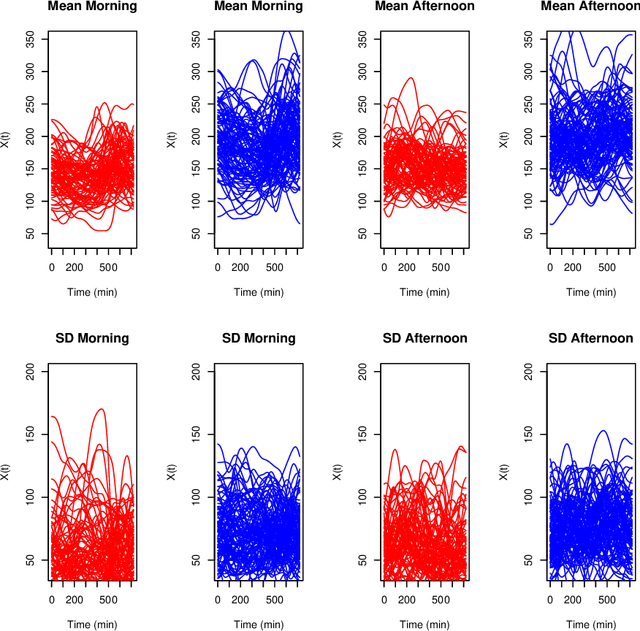
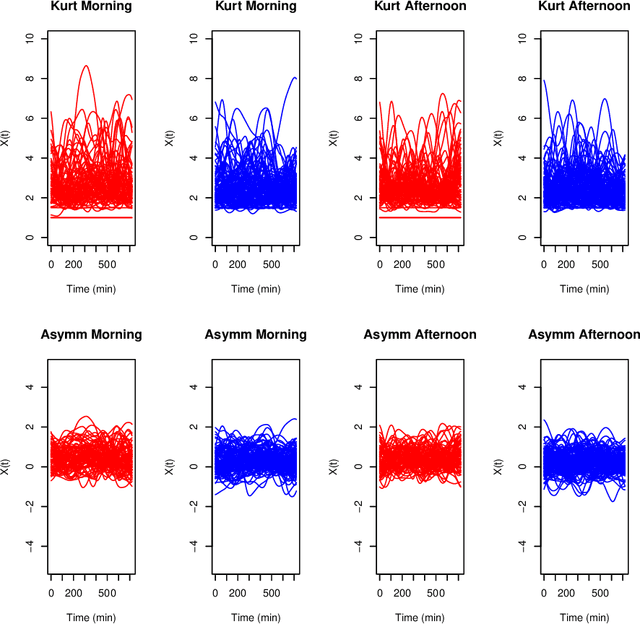
Biclustering algorithms partition data and covariates simultaneously, providing new insights in several domains, such as analyzing gene expression to discover new biological functions. This paper develops a new model-free biclustering algorithm in abstract spaces using the notions of energy distance (ED) and the maximum mean discrepancy (MMD) -- two distances between probability distributions capable of handling complex data such as curves or graphs. The proposed method can learn more general and complex cluster shapes than most existing literature approaches, which usually focus on detecting mean and variance differences. Although the biclustering configurations of our approach are constrained to create disjoint structures at the datum and covariate levels, the results are competitive. Our results are similar to state-of-the-art methods in their optimal scenarios, assuming a proper kernel choice, outperforming them when cluster differences are concentrated in higher-order moments. The model's performance has been tested in several situations that involve simulated and real-world datasets. Finally, new theoretical consistency results are established using some tools of the theory of optimal transport.

Neural interval-censored Cox regression with feature selection

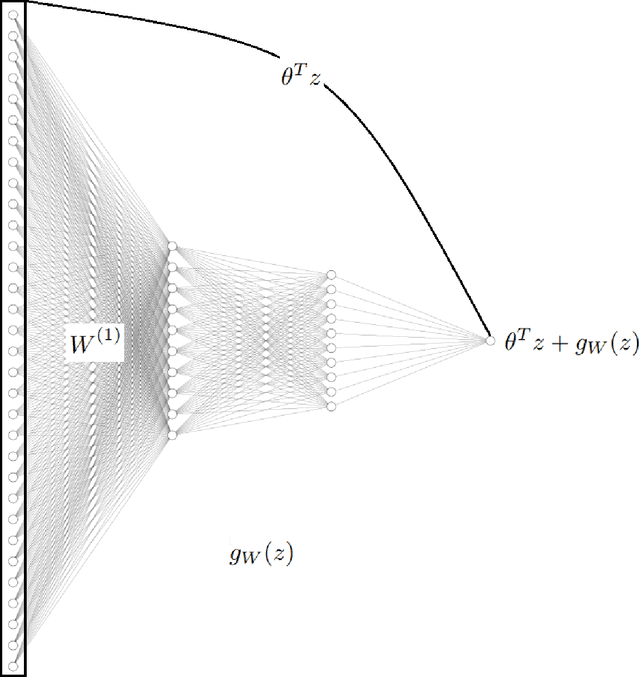
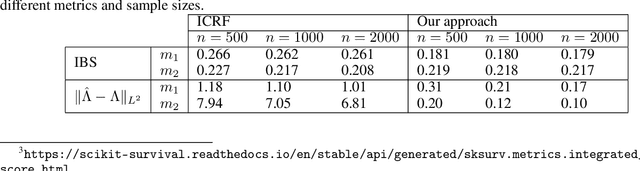
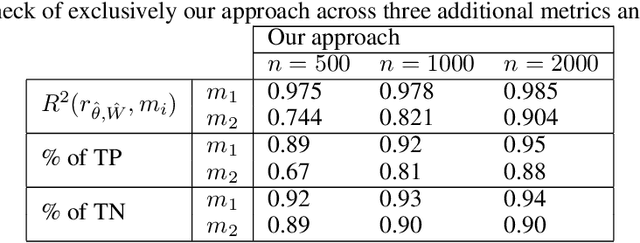
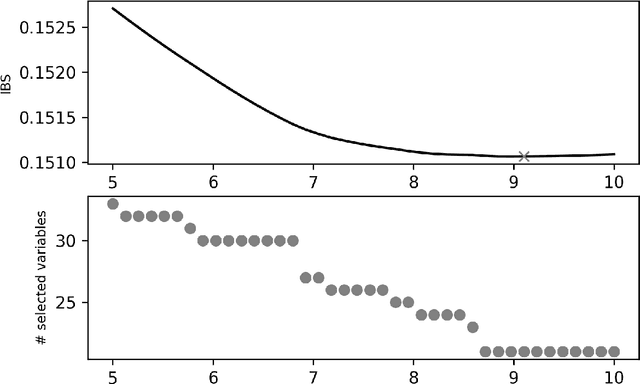
The classical Cox model emerged in 1972 promoting breakthroughs in how patient prognosis is quantified using time-to-event analysis in biomedicine. One of the most useful characteristics of the model for practitioners is the interpretability of the variables in the analysis. However, this comes at the price of introducing strong assumptions concerning the functional form of the regression model. To break this gap, this paper aims to exploit the explainability advantages of the classical Cox model in the setting of interval-censoring using a new Lasso neural network that simultaneously selects the most relevant variables while quantifying non-linear relations between predictors and survival times. The gain of the new method is illustrated empirically in an extensive simulation study with examples that involve linear and non-linear ground dependencies. We also demonstrate the performance of our strategy in the analysis of physiological, clinical and accelerometer data from the NHANES 2003-2006 waves to predict the effect of physical activity on the survival of patients. Our method outperforms the prior results in the literature that use the traditional Cox model.

Hypothesis testing for matched pairs with missing data by maximum mean discrepancy: An application to continuous glucose monitoring

A frequent problem in statistical science is how to properly handle missing data in matched paired observations. There is a large body of literature coping with the univariate case. Yet, the ongoing technological progress in measuring biological systems raises the need for addressing more complex data, e.g., graphs, strings and probability distributions, among others. In order to fill this gap, this paper proposes new estimators of the maximum mean discrepancy (MMD) to handle complex matched pairs with missing data. These estimators can detect differences in data distributions under different missingness mechanisms. The validity of this approach is proven and further studied in an extensive simulation study, and results of statistical consistency are provided. Data from continuous glucose monitoring in a longitudinal population-based diabetes study are used to illustrate the application of this approach. By employing the new distributional representations together with cluster analysis, new clinical criteria on how glucose changes vary at the distributional level over five years can be explored.