A Central Limit Theorem for the permutation importance measure

Random Forests have become a widely used tool in machine learning since their introduction in 2001, known for their strong performance in classification and regression tasks. One key feature of Random Forests is the Random Forest Permutation Importance Measure (RFPIM), an internal, non-parametric measure of variable importance. While widely used, theoretical work on RFPIM is sparse, and most research has focused on empirical findings. However, recent progress has been made, such as establishing consistency of the RFPIM, although a mathematical analysis of its asymptotic distribution is still missing. In this paper, we provide a formal proof of a Central Limit Theorem for RFPIM using U-Statistics theory. Our approach deviates from the conventional Random Forest model by assuming a random number of trees and imposing conditions on the regression functions and error terms, which must be bounded and additive, respectively. Our result aims at improving the theoretical understanding of RFPIM rather than conducting comprehensive hypothesis testing. However, our contributions provide a solid foundation and demonstrate the potential for future work to extend to practical applications which we also highlight with a small simulation study.

A Multiple kernel testing procedure for non-proportional hazards in factorial designs

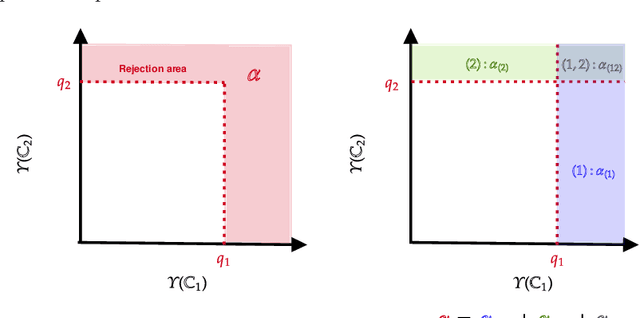
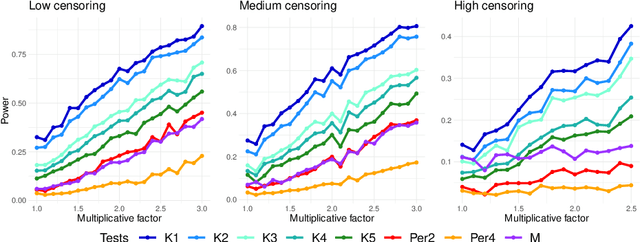
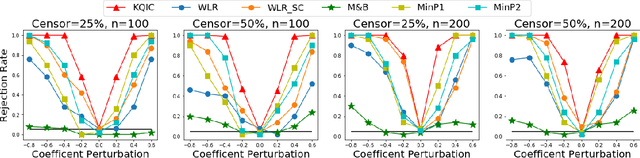
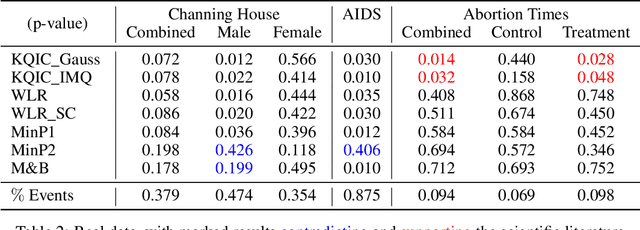
In this paper we propose a Multiple kernel testing procedure to infer survival data when several factors (e.g. different treatment groups, gender, medical history) and their interaction are of interest simultaneously. Our method is able to deal with complex data and can be seen as an alternative to the omnipresent Cox model when assumptions such as proportionality cannot be justified. Our methodology combines well-known concepts from Survival Analysis, Machine Learning and Multiple Testing: differently weighted log-rank tests, kernel methods and multiple contrast tests. By that, complex hazard alternatives beyond the classical proportional hazard set-up can be detected. Moreover, multiple comparisons are performed by fully exploiting the dependence structure of the single testing procedures to avoid a loss of power. In all, this leads to a flexible and powerful procedure for factorial survival designs whose theoretical validity is proven by martingale arguments and the theory for $V$-statistics. We evaluate the performance of our method in an extensive simulation study and illustrate it by a real data analysis.

Hypothesis testing for matched pairs with missing data by maximum mean discrepancy: An application to continuous glucose monitoring

A frequent problem in statistical science is how to properly handle missing data in matched paired observations. There is a large body of literature coping with the univariate case. Yet, the ongoing technological progress in measuring biological systems raises the need for addressing more complex data, e.g., graphs, strings and probability distributions, among others. In order to fill this gap, this paper proposes new estimators of the maximum mean discrepancy (MMD) to handle complex matched pairs with missing data. These estimators can detect differences in data distributions under different missingness mechanisms. The validity of this approach is proven and further studied in an extensive simulation study, and results of statistical consistency are provided. Data from continuous glucose monitoring in a longitudinal population-based diabetes study are used to illustrate the application of this approach. By employing the new distributional representations together with cluster analysis, new clinical criteria on how glucose changes vary at the distributional level over five years can be explored.

A kernel test for quasi-independence

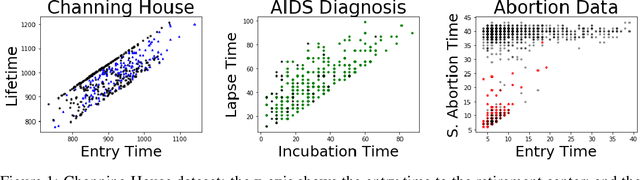
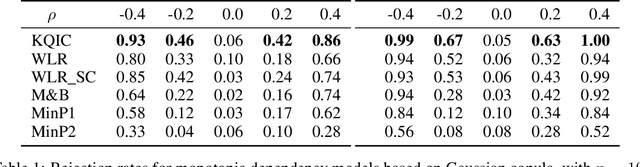
We consider settings in which the data of interest correspond to pairs of ordered times, e.g, the birth times of the first and second child, the times at which a new user creates an account and makes the first purchase on a website, and the entry and survival times of patients in a clinical trial. In these settings, the two times are not independent (the second occurs after the first), yet it is still of interest to determine whether there exists significant dependence {\em beyond} their ordering in time. We refer to this notion as "quasi-(in)dependence". For instance, in a clinical trial, to avoid biased selection, we might wish to verify that recruitment times are quasi-independent of survival times, where dependencies might arise due to seasonal effects. In this paper, we propose a nonparametric statistical test of quasi-independence. Our test considers a potentially infinite space of alternatives, making it suitable for complex data where the nature of the possible quasi-dependence is not known in advance. Standard parametric approaches are recovered as special cases, such as the classical conditional Kendall's tau, and log-rank tests. The tests apply in the right-censored setting: an essential feature in clinical trials, where patients can withdraw from the study. We provide an asymptotic analysis of our test-statistic, and demonstrate in experiments that our test obtains better power than existing approaches, while being more computationally efficient.