A Multiple kernel testing procedure for non-proportional hazards in factorial designs

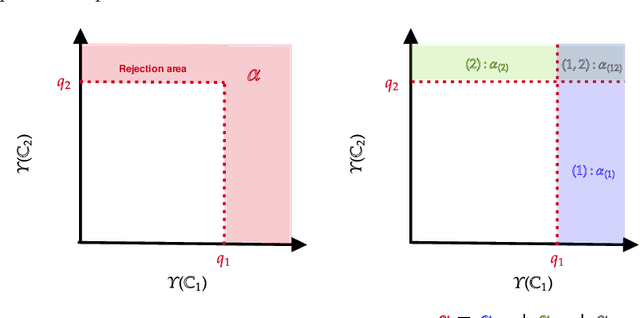
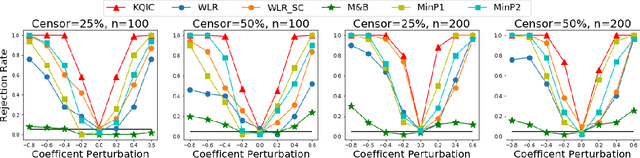
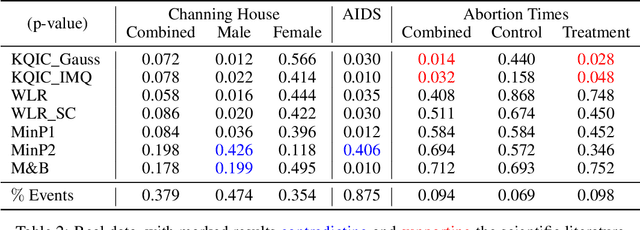
In this paper we propose a Multiple kernel testing procedure to infer survival data when several factors (e.g. different treatment groups, gender, medical history) and their interaction are of interest simultaneously. Our method is able to deal with complex data and can be seen as an alternative to the omnipresent Cox model when assumptions such as proportionality cannot be justified. Our methodology combines well-known concepts from Survival Analysis, Machine Learning and Multiple Testing: differently weighted log-rank tests, kernel methods and multiple contrast tests. By that, complex hazard alternatives beyond the classical proportional hazard set-up can be detected. Moreover, multiple comparisons are performed by fully exploiting the dependence structure of the single testing procedures to avoid a loss of power. In all, this leads to a flexible and powerful procedure for factorial survival designs whose theoretical validity is proven by martingale arguments and the theory for $V$-statistics. We evaluate the performance of our method in an extensive simulation study and illustrate it by a real data analysis.

A kernel test for quasi-independence

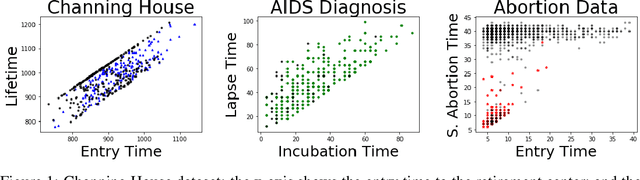
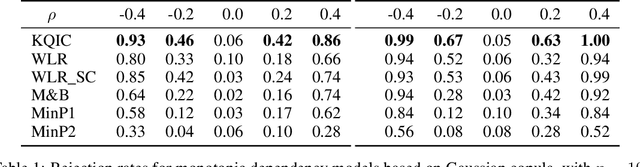
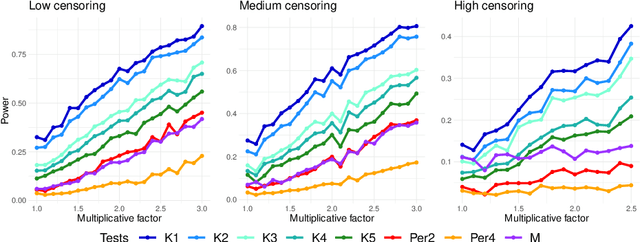
We consider settings in which the data of interest correspond to pairs of ordered times, e.g, the birth times of the first and second child, the times at which a new user creates an account and makes the first purchase on a website, and the entry and survival times of patients in a clinical trial. In these settings, the two times are not independent (the second occurs after the first), yet it is still of interest to determine whether there exists significant dependence {\em beyond} their ordering in time. We refer to this notion as "quasi-(in)dependence". For instance, in a clinical trial, to avoid biased selection, we might wish to verify that recruitment times are quasi-independent of survival times, where dependencies might arise due to seasonal effects. In this paper, we propose a nonparametric statistical test of quasi-independence. Our test considers a potentially infinite space of alternatives, making it suitable for complex data where the nature of the possible quasi-dependence is not known in advance. Standard parametric approaches are recovered as special cases, such as the classical conditional Kendall's tau, and log-rank tests. The tests apply in the right-censored setting: an essential feature in clinical trials, where patients can withdraw from the study. We provide an asymptotic analysis of our test-statistic, and demonstrate in experiments that our test obtains better power than existing approaches, while being more computationally efficient.

Gaussian Processes for Survival Analysis

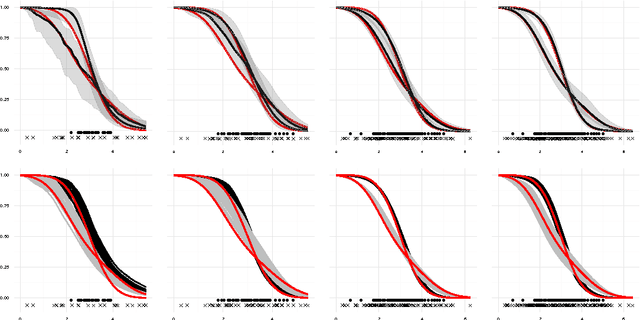
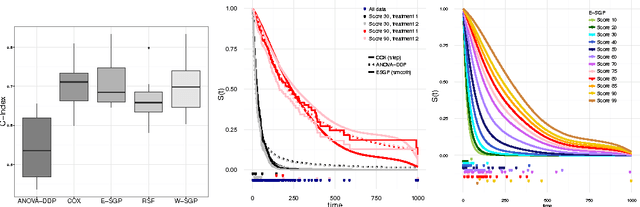
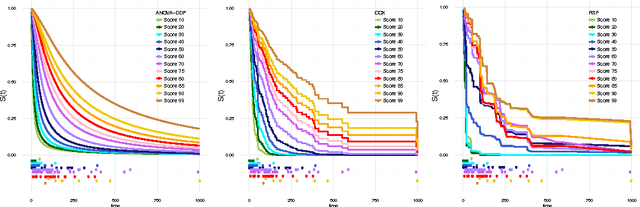
We introduce a semi-parametric Bayesian model for survival analysis. The model is centred on a parametric baseline hazard, and uses a Gaussian process to model variations away from it nonparametrically, as well as dependence on covariates. As opposed to many other methods in survival analysis, our framework does not impose unnecessary constraints in the hazard rate or in the survival function. Furthermore, our model handles left, right and interval censoring mechanisms common in survival analysis. We propose a MCMC algorithm to perform inference and an approximation scheme based on random Fourier features to make computations faster. We report experimental results on synthetic and real data, showing that our model performs better than competing models such as Cox proportional hazards, ANOVA-DDP and random survival forests.