A Multiple kernel testing procedure for non-proportional hazards in factorial designs

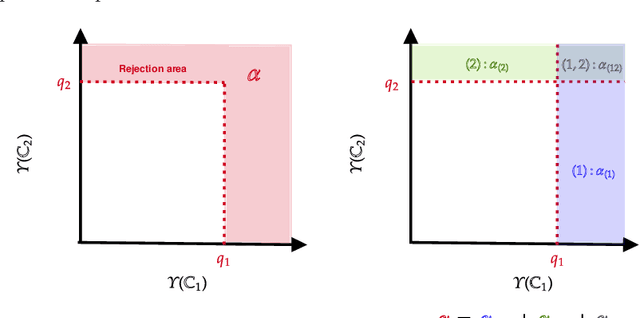
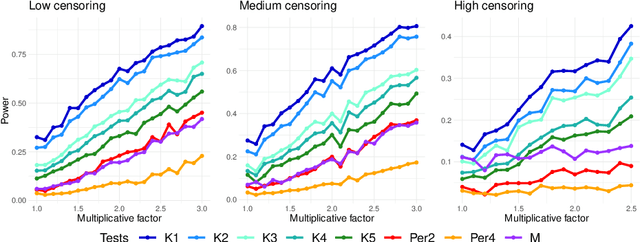
In this paper we propose a Multiple kernel testing procedure to infer survival data when several factors (e.g. different treatment groups, gender, medical history) and their interaction are of interest simultaneously. Our method is able to deal with complex data and can be seen as an alternative to the omnipresent Cox model when assumptions such as proportionality cannot be justified. Our methodology combines well-known concepts from Survival Analysis, Machine Learning and Multiple Testing: differently weighted log-rank tests, kernel methods and multiple contrast tests. By that, complex hazard alternatives beyond the classical proportional hazard set-up can be detected. Moreover, multiple comparisons are performed by fully exploiting the dependence structure of the single testing procedures to avoid a loss of power. In all, this leads to a flexible and powerful procedure for factorial survival designs whose theoretical validity is proven by martingale arguments and the theory for $V$-statistics. We evaluate the performance of our method in an extensive simulation study and illustrate it by a real data analysis.

Gaussian Processes for Survival Analysis

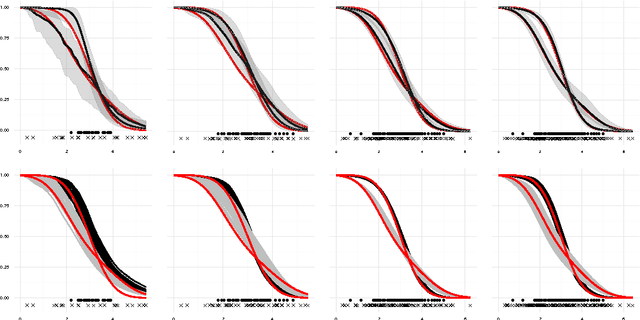
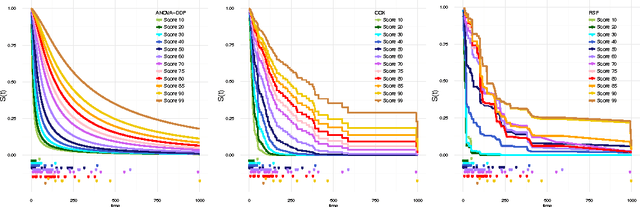
We introduce a semi-parametric Bayesian model for survival analysis. The model is centred on a parametric baseline hazard, and uses a Gaussian process to model variations away from it nonparametrically, as well as dependence on covariates. As opposed to many other methods in survival analysis, our framework does not impose unnecessary constraints in the hazard rate or in the survival function. Furthermore, our model handles left, right and interval censoring mechanisms common in survival analysis. We propose a MCMC algorithm to perform inference and an approximation scheme based on random Fourier features to make computations faster. We report experimental results on synthetic and real data, showing that our model performs better than competing models such as Cox proportional hazards, ANOVA-DDP and random survival forests.