A Multiple kernel testing procedure for non-proportional hazards in factorial designs
Paper and Code
Jun 15, 2022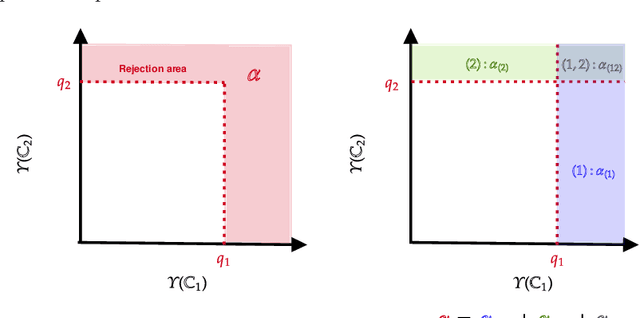

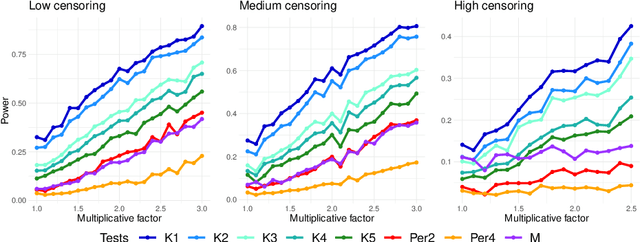

In this paper we propose a Multiple kernel testing procedure to infer survival data when several factors (e.g. different treatment groups, gender, medical history) and their interaction are of interest simultaneously. Our method is able to deal with complex data and can be seen as an alternative to the omnipresent Cox model when assumptions such as proportionality cannot be justified. Our methodology combines well-known concepts from Survival Analysis, Machine Learning and Multiple Testing: differently weighted log-rank tests, kernel methods and multiple contrast tests. By that, complex hazard alternatives beyond the classical proportional hazard set-up can be detected. Moreover, multiple comparisons are performed by fully exploiting the dependence structure of the single testing procedures to avoid a loss of power. In all, this leads to a flexible and powerful procedure for factorial survival designs whose theoretical validity is proven by martingale arguments and the theory for $V$-statistics. We evaluate the performance of our method in an extensive simulation study and illustrate it by a real data analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge