A Central Limit Theorem for the permutation importance measure

Random Forests have become a widely used tool in machine learning since their introduction in 2001, known for their strong performance in classification and regression tasks. One key feature of Random Forests is the Random Forest Permutation Importance Measure (RFPIM), an internal, non-parametric measure of variable importance. While widely used, theoretical work on RFPIM is sparse, and most research has focused on empirical findings. However, recent progress has been made, such as establishing consistency of the RFPIM, although a mathematical analysis of its asymptotic distribution is still missing. In this paper, we provide a formal proof of a Central Limit Theorem for RFPIM using U-Statistics theory. Our approach deviates from the conventional Random Forest model by assuming a random number of trees and imposing conditions on the regression functions and error terms, which must be bounded and additive, respectively. Our result aims at improving the theoretical understanding of RFPIM rather than conducting comprehensive hypothesis testing. However, our contributions provide a solid foundation and demonstrate the potential for future work to extend to practical applications which we also highlight with a small simulation study.

TREE: Tree Regularization for Efficient Execution

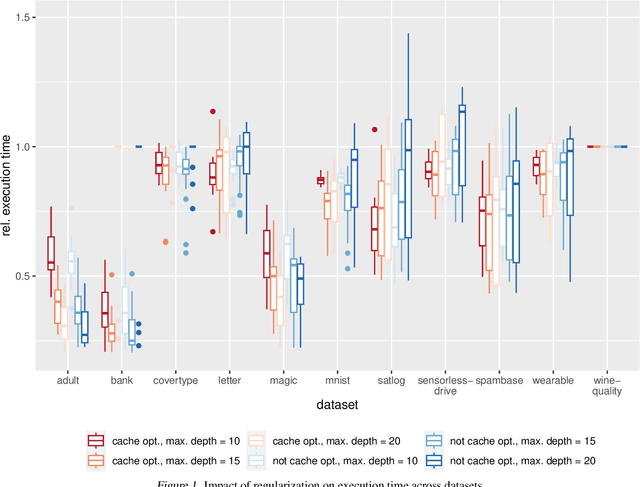
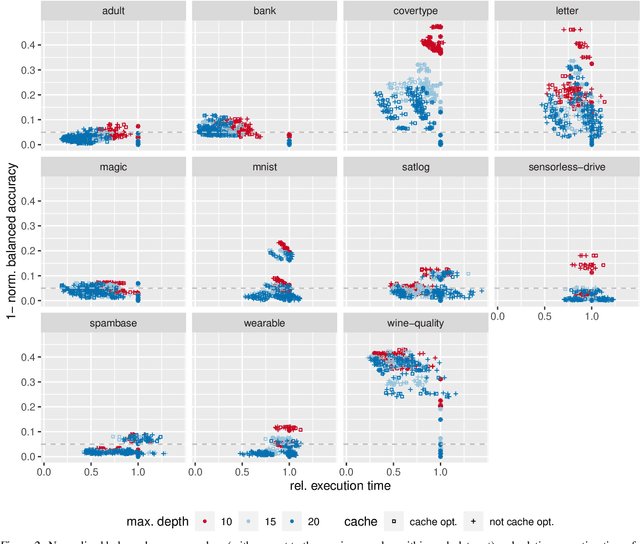
The rise of machine learning methods on heavily resource constrained devices requires not only the choice of a suitable model architecture for the target platform, but also the optimization of the chosen model with regard to execution time consumption for inference in order to optimally utilize the available resources. Random forests and decision trees are shown to be a suitable model for such a scenario, since they are not only heavily tunable towards the total model size, but also offer a high potential for optimizing their executions according to the underlying memory architecture. In addition to the straightforward strategy of enforcing shorter paths through decision trees and hence reducing the execution time for inference, hardware-aware implementations can optimize the execution time in an orthogonal manner. One particular hardware-aware optimization is to layout the memory of decision trees in such a way, that higher probably paths are less likely to be evicted from system caches. This works particularly well when splits within tree nodes are uneven and have a high probability to visit one of the child nodes. In this paper, we present a method to reduce path lengths by rewarding uneven probability distributions during the training of decision trees at the cost of a minimal accuracy degradation. Specifically, we regularize the impurity computation of the CART algorithm in order to favor not only low impurity, but also highly asymmetric distributions for the evaluation of split criteria and hence offer a high optimization potential for a memory architecture-aware implementation. We show that especially for binary classification data sets and data sets with many samples, this form of regularization can lead to an reduction of up to approximately four times in the execution time with a minimal accuracy degradation.

Comparing statistical and machine learning methods for time series forecasting in data-driven logistics -- A simulation study

Many planning and decision activities in logistics and supply chain management are based on forecasts of multiple time dependent factors. Therefore, the quality of planning depends on the quality of the forecasts. We compare various forecasting methods in terms of out of the box forecasting performance on a broad set of simulated time series. We simulate various linear and non-linear time series and look at the one step forecast performance of statistical learning methods.

Dataset Bias in Human Activity Recognition

When creating multi-channel time-series datasets for Human Activity Recognition (HAR), researchers are faced with the issue of subject selection criteria. It is unknown what physical characteristics and/or soft-biometrics, such as age, height, and weight, need to be taken into account to train a classifier to achieve robustness towards heterogeneous populations in the training and testing data. This contribution statistically curates the training data to assess to what degree the physical characteristics of humans influence HAR performance. We evaluate the performance of a state-of-the-art convolutional neural network on two HAR datasets that vary in the sensors, activities, and recording for time-series HAR. The training data is intentionally biased with respect to human characteristics to determine the features that impact motion behaviour. The evaluations brought forth the impact of the subjects' characteristics on HAR. Thus, providing insights regarding the robustness of the classifier with respect to heterogeneous populations. The study is a step forward in the direction of fair and trustworthy artificial intelligence by attempting to quantify representation bias in multi-channel time series HAR data.

Machine Learning for Multi-Output Regression: When should a holistic multivariate approach be preferred over separate univariate ones?

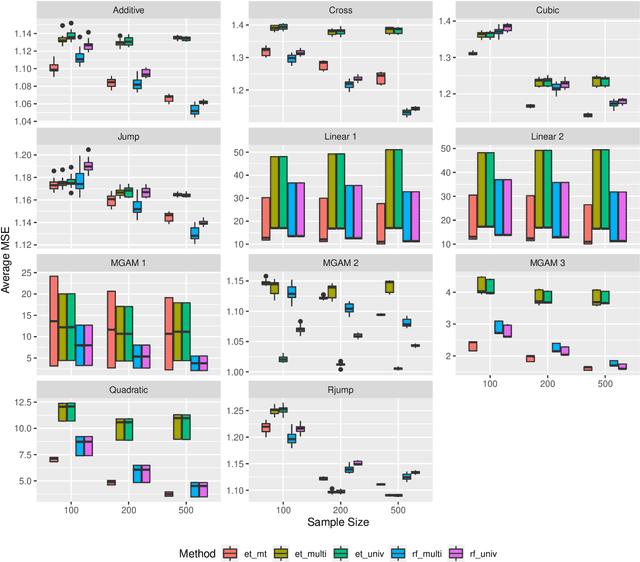
Tree-based ensembles such as the Random Forest are modern classics among statistical learning methods. In particular, they are used for predicting univariate responses. In case of multiple outputs the question arises whether we separately fit univariate models or directly follow a multivariate approach. For the latter, several possibilities exist that are, e.g. based on modified splitting or stopping rules for multi-output regression. In this work we compare these methods in extensive simulations to help in answering the primary question when to use multivariate ensemble techniques.