Conformal Prediction in Dynamic Biological Systems
Paper and Code
Sep 04, 2024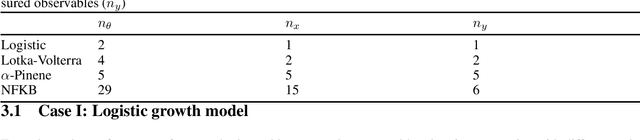


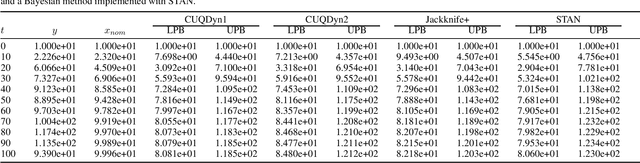
Uncertainty quantification (UQ) is the process of systematically determining and characterizing the degree of confidence in computational model predictions. In the context of systems biology, especially with dynamic models, UQ is crucial because it addresses the challenges posed by nonlinearity and parameter sensitivity, allowing us to properly understand and extrapolate the behavior of complex biological systems. Here, we focus on dynamic models represented by deterministic nonlinear ordinary differential equations. Many current UQ approaches in this field rely on Bayesian statistical methods. While powerful, these methods often require strong prior specifications and make parametric assumptions that may not always hold in biological systems. Additionally, these methods face challenges in domains where sample sizes are limited, and statistical inference becomes constrained, with computational speed being a bottleneck in large models of biological systems. As an alternative, we propose the use of conformal inference methods, introducing two novel algorithms that, in some instances, offer non-asymptotic guarantees, enhancing robustness and scalability across various applications. We demonstrate the efficacy of our proposed algorithms through several scenarios, highlighting their advantages over traditional Bayesian approaches. The proposed methods show promising results for diverse biological data structures and scenarios, offering a general framework to quantify uncertainty for dynamic models of biological systems.The software for the methodology and the reproduction of the results is available at https://zenodo.org/doi/10.5281/zenodo.13644870.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge