Duyeol Lee
Discussion of Multiscale Fisher's Independence Test for Multivariate Dependence
Apr 26, 2022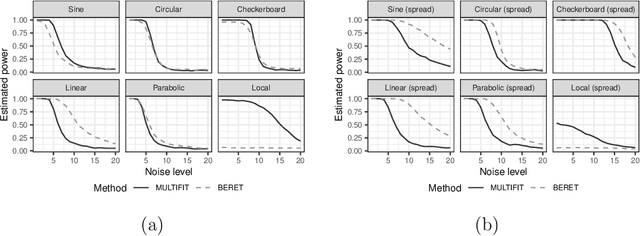
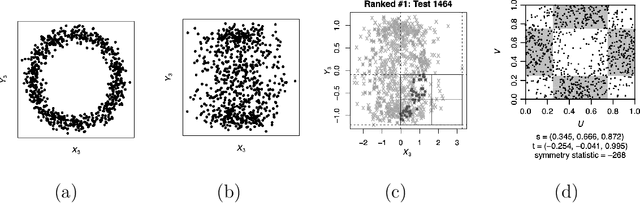
Abstract:The multiscale Fisher's independence test (MULTIFIT hereafter) proposed by Gorsky & Ma (2022) is a novel method to test independence between two random vectors. By its design, this test is particularly useful in detecting local dependence. Moreover, by adopting a resampling-free approach, it can easily accommodate massive sample sizes. Another benefit of the proposed method is its ability to interpret the nature of dependency. We congratulate the authors, Shai Gorksy and Li Ma, for their very interesting and elegant work. In this comment, we would like to discuss a general framework unifying the MULTIFIT and other tests and compare it with the binary expansion randomized ensemble test (BERET hereafter) proposed by Lee et al. (In press). We also would like to contribute our thoughts on potential extensions of the method.
Testing Independence with the Binary Expansion Randomized Ensemble Test
Dec 11, 2019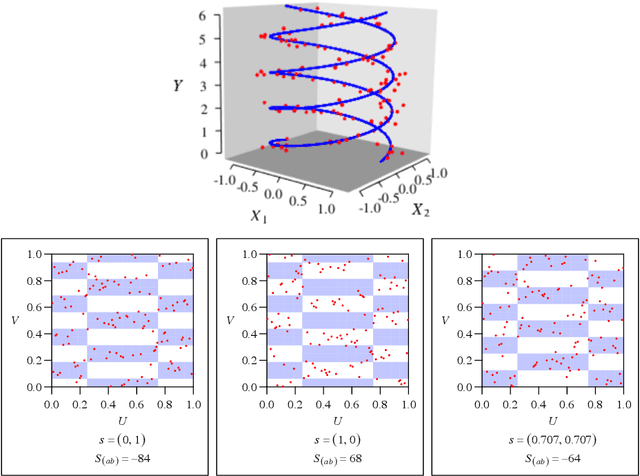
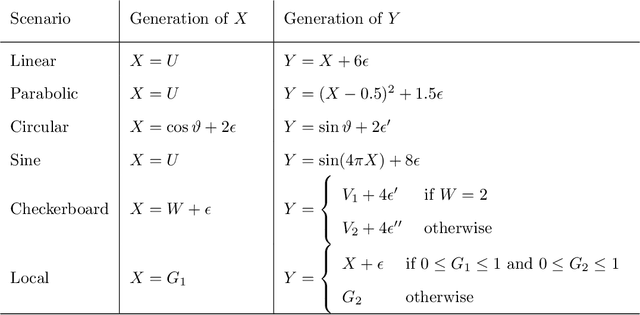
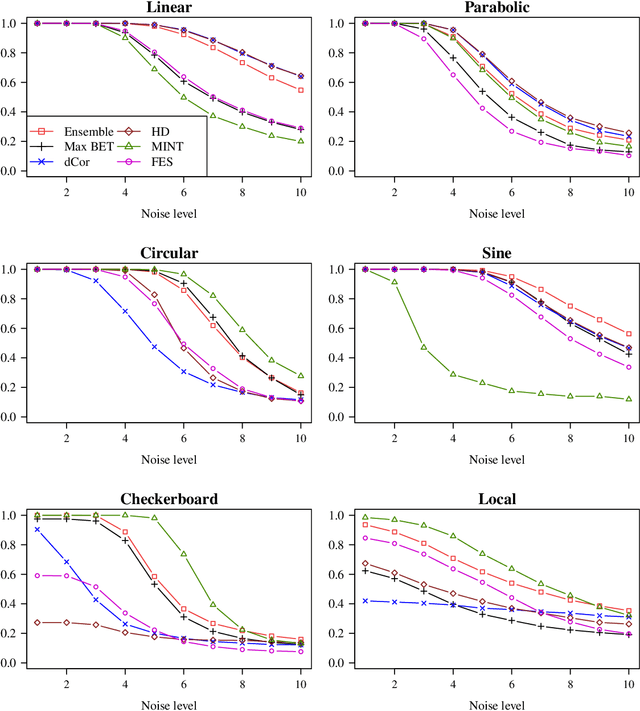

Abstract:Recently, the binary expansion testing framework was introduced to test the independence of two continuous random variables by utilizing symmetry statistics that are complete sufficient statistics for dependence. We develop a new test by an ensemble method that uses the sum of squared symmetry statistics and distance correlation. Simulation studies suggest that this method improves the power while preserving the clear interpretation of the binary expansion testing. We extend this method to tests of independence of random vectors in arbitrary dimension. By random projections, the proposed binary expansion randomized ensemble test transforms the multivariate independence testing problem into a univariate problem. Simulation studies and data example analyses show that the proposed method provides relatively robust performance compared with existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge