TransformerLSR: Attentive Joint Model of Longitudinal Data, Survival, and Recurrent Events with Concurrent Latent Structure

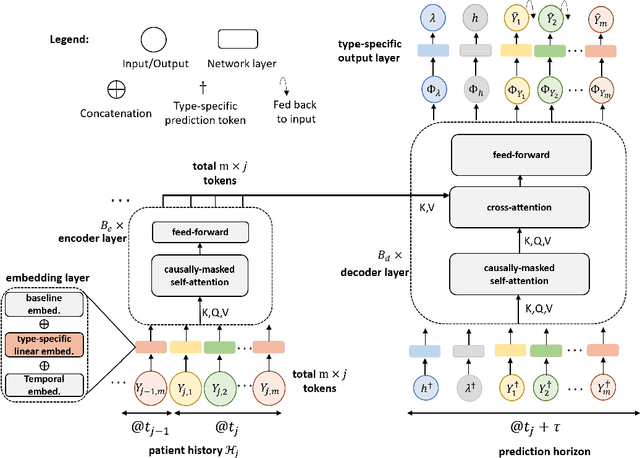
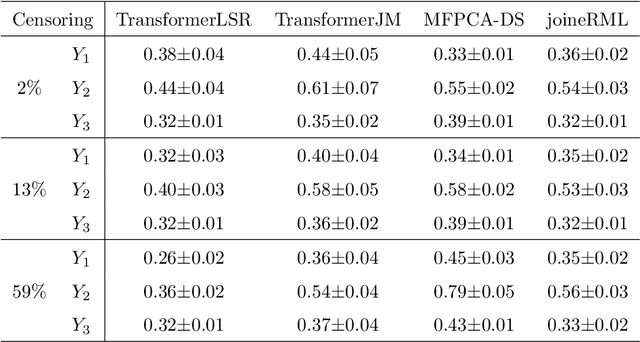
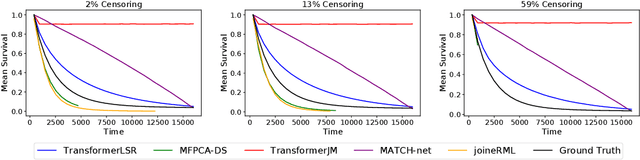
In applications such as biomedical studies, epidemiology, and social sciences, recurrent events often co-occur with longitudinal measurements and a terminal event, such as death. Therefore, jointly modeling longitudinal measurements, recurrent events, and survival data while accounting for their dependencies is critical. While joint models for the three components exist in statistical literature, many of these approaches are limited by heavy parametric assumptions and scalability issues. Recently, incorporating deep learning techniques into joint modeling has shown promising results. However, current methods only address joint modeling of longitudinal measurements at regularly-spaced observation times and survival events, neglecting recurrent events. In this paper, we develop TransformerLSR, a flexible transformer-based deep modeling and inference framework to jointly model all three components simultaneously. TransformerLSR integrates deep temporal point processes into the joint modeling framework, treating recurrent and terminal events as two competing processes dependent on past longitudinal measurements and recurrent event times. Additionally, TransformerLSR introduces a novel trajectory representation and model architecture to potentially incorporate a priori knowledge of known latent structures among concurrent longitudinal variables. We demonstrate the effectiveness and necessity of TransformerLSR through simulation studies and analyzing a real-world medical dataset on patients after kidney transplantation.

MoMA: Model-based Mirror Ascent for Offline Reinforcement Learning

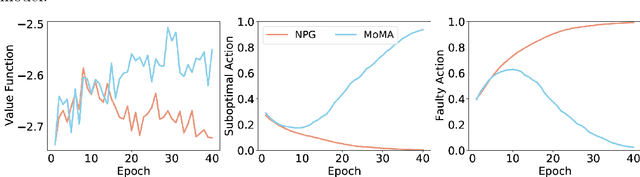
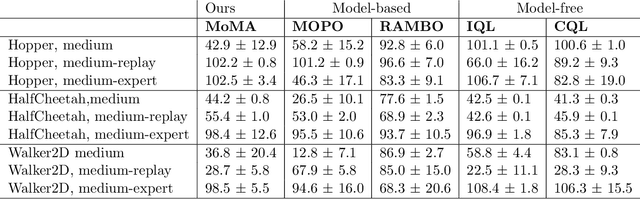
Model-based offline reinforcement learning methods (RL) have achieved state-of-the-art performance in many decision-making problems thanks to their sample efficiency and generalizability. Despite these advancements, existing model-based offline RL approaches either focus on theoretical studies without developing practical algorithms or rely on a restricted parametric policy space, thus not fully leveraging the advantages of an unrestricted policy space inherent to model-based methods. To address this limitation, we develop MoMA, a model-based mirror ascent algorithm with general function approximations under partial coverage of offline data. MoMA distinguishes itself from existing literature by employing an unrestricted policy class. In each iteration, MoMA conservatively estimates the value function by a minimization procedure within a confidence set of transition models in the policy evaluation step, then updates the policy with general function approximations instead of commonly-used parametric policy classes in the policy improvement step. Under some mild assumptions, we establish theoretical guarantees of MoMA by proving an upper bound on the suboptimality of the returned policy. We also provide a practically implementable, approximate version of the algorithm. The effectiveness of MoMA is demonstrated via numerical studies.

A Scalable Framework for Sparse Clustering Without Shrinkage

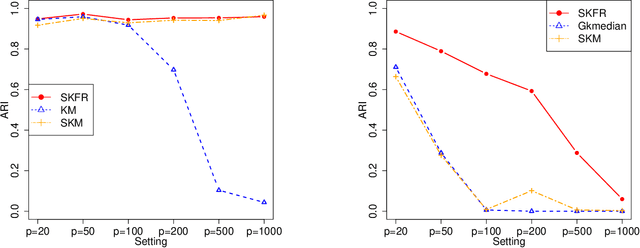
Clustering, a fundamental activity in unsupervised learning, is notoriously difficult when the feature space is high-dimensional. Fortunately, in many realistic scenarios, only a handful of features are relevant in distinguishing clusters. This has motivated the development of sparse clustering techniques that typically rely on k-means within outer algorithms of high computational complexity. Current techniques also require careful tuning of shrinkage parameters, further limiting their scalability. In this paper, we propose a novel framework for sparse k-means clustering that is intuitive, simple to implement, and competitive with state-of-the-art algorithms. We show that our algorithm enjoys consistency and convergence guarantees. Our core method readily generalizes to several task-specific algorithms such as clustering on subsets of attributes and in partially observed data settings. We showcase these contributions via simulated experiments and benchmark datasets, as well as a case study on mouse protein expression.