Extensions to the Proximal Distance of Method of Constrained Optimization

The current paper studies the problem of minimizing a loss $f(\boldsymbol{x})$ subject to constraints of the form $\boldsymbol{D}\boldsymbol{x} \in S$, where $S$ is a closed set, convex or not, and $\boldsymbol{D}$ is a fusion matrix. Fusion constraints can capture smoothness, sparsity, or more general constraint patterns. To tackle this generic class of problems, we combine the Beltrami-Courant penalty method of optimization with the proximal distance principle. The latter is driven by minimization of penalized objectives $f(\boldsymbol{x})+\frac{\rho}{2}\text{dist}(\boldsymbol{D}\boldsymbol{x},S)^2$ involving large tuning constants $\rho$ and the squared Euclidean distance of $\boldsymbol{D}\boldsymbol{x}$ from $S$. The next iterate $\boldsymbol{x}_{n+1}$ of the corresponding proximal distance algorithm is constructed from the current iterate $\boldsymbol{x}_n$ by minimizing the majorizing surrogate function $f(\boldsymbol{x})+\frac{\rho}{2}\|\boldsymbol{D}\boldsymbol{x}-\mathcal{P}_S(\boldsymbol{D}\boldsymbol{x}_n)\|^2$. For fixed $\rho$ and convex $f(\boldsymbol{x})$ and $S$, we prove convergence, provide convergence rates, and demonstrate linear convergence under stronger assumptions. We also construct a steepest descent (SD) variant to avoid costly linear system solves. To benchmark our algorithms, we adapt the alternating direction method of multipliers (ADMM) and compare on extensive numerical tests including problems in metric projection, convex regression, convex clustering, total variation image denoising, and projection of a matrix to one that has a good condition number. Our experiments demonstrate the superior speed and acceptable accuracy of the steepest variant on high-dimensional problems. Julia code to replicate all of our experiments can be found at https://github.com/alanderos91/ProximalDistanceAlgorithms.jl.

A Scalable Framework for Sparse Clustering Without Shrinkage

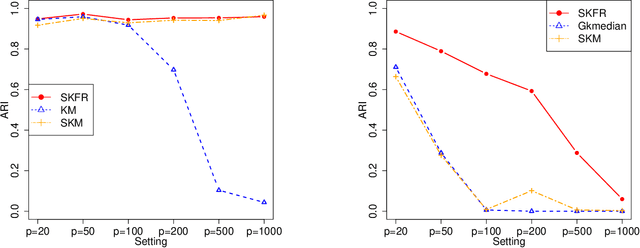
Clustering, a fundamental activity in unsupervised learning, is notoriously difficult when the feature space is high-dimensional. Fortunately, in many realistic scenarios, only a handful of features are relevant in distinguishing clusters. This has motivated the development of sparse clustering techniques that typically rely on k-means within outer algorithms of high computational complexity. Current techniques also require careful tuning of shrinkage parameters, further limiting their scalability. In this paper, we propose a novel framework for sparse k-means clustering that is intuitive, simple to implement, and competitive with state-of-the-art algorithms. We show that our algorithm enjoys consistency and convergence guarantees. Our core method readily generalizes to several task-specific algorithms such as clustering on subsets of attributes and in partially observed data settings. We showcase these contributions via simulated experiments and benchmark datasets, as well as a case study on mouse protein expression.

Generalized Linear Model Regression under Distance-to-set Penalties

Estimation in generalized linear models (GLM) is complicated by the presence of constraints. One can handle constraints by maximizing a penalized log-likelihood. Penalties such as the lasso are effective in high dimensions, but often lead to unwanted shrinkage. This paper explores instead penalizing the squared distance to constraint sets. Distance penalties are more flexible than algebraic and regularization penalties, and avoid the drawback of shrinkage. To optimize distance penalized objectives, we make use of the majorization-minimization principle. Resulting algorithms constructed within this framework are amenable to acceleration and come with global convergence guarantees. Applications to shape constraints, sparse regression, and rank-restricted matrix regression on synthetic and real data showcase strong empirical performance, even under non-convex constraints.

Iterative Hard Thresholding for Model Selection in Genome-Wide Association Studies

A genome-wide association study (GWAS) correlates marker variation with trait variation in a sample of individuals. Each study subject is genotyped at a multitude of SNPs (single nucleotide polymorphisms) spanning the genome. Here we assume that subjects are unrelated and collected at random and that trait values are normally distributed or transformed to normality. Over the past decade, researchers have been remarkably successful in applying GWAS analysis to hundreds of traits. The massive amount of data produced in these studies present unique computational challenges. Penalized regression with LASSO or MCP penalties is capable of selecting a handful of associated SNPs from millions of potential SNPs. Unfortunately, model selection can be corrupted by false positives and false negatives, obscuring the genetic underpinning of a trait. This paper introduces the iterative hard thresholding (IHT) algorithm to the GWAS analysis of continuous traits. Our parallel implementation of IHT accommodates SNP genotype compression and exploits multiple CPU cores and graphics processing units (GPUs). This allows statistical geneticists to leverage commodity desktop computers in GWAS analysis and to avoid supercomputing. We evaluate IHT performance on both simulated and real GWAS data and conclude that it reduces false positive and false negative rates while remaining competitive in computational time with penalized regression. Source code is freely available at https://github.com/klkeys/IHT.jl.

An MM Algorithm for Split Feasibility Problems

The classical multi-set split feasibility problem seeks a point in the intersection of finitely many closed convex domain constraints, whose image under a linear mapping also lies in the intersection of finitely many closed convex range constraints. Split feasibility generalizes important inverse problems including convex feasibility, linear complementarity, and regression with constraint sets. When a feasible point does not exist, solution methods that proceed by minimizing a proximity function can be used to obtain optimal approximate solutions to the problem. We present an extension of the proximity function approach that generalizes the linear split feasibility problem to allow for non-linear mappings. Our algorithm is based on the principle of majorization-minimization, is amenable to quasi-Newton acceleration, and comes complete with convergence guarantees under mild assumptions. Furthermore, we show that the Euclidean norm appearing in the proximity function of the non-linear split feasibility problem can be replaced by arbitrary Bregman divergences. We explore several examples illustrating the merits of non-linear formulations over the linear case, with a focus on optimization for intensity-modulated radiation therapy.

Splitting Methods for Convex Clustering

Clustering is a fundamental problem in many scientific applications. Standard methods such as $k$-means, Gaussian mixture models, and hierarchical clustering, however, are beset by local minima, which are sometimes drastically suboptimal. Recently introduced convex relaxations of $k$-means and hierarchical clustering shrink cluster centroids toward one another and ensure a unique global minimizer. In this work we present two splitting methods for solving the convex clustering problem. The first is an instance of the alternating direction method of multipliers (ADMM); the second is an instance of the alternating minimization algorithm (AMA). In contrast to previously considered algorithms, our ADMM and AMA formulations provide simple and unified frameworks for solving the convex clustering problem under the previously studied norms and open the door to potentially novel norms. We demonstrate the performance of our algorithm on both simulated and real data examples. While the differences between the two algorithms appear to be minor on the surface, complexity analysis and numerical experiments show AMA to be significantly more efficient.

Distance Majorization and Its Applications

The problem of minimizing a continuously differentiable convex function over an intersection of closed convex sets is ubiquitous in applied mathematics. It is particularly interesting when it is easy to project onto each separate set, but nontrivial to project onto their intersection. Algorithms based on Newton's method such as the interior point method are viable for small to medium-scale problems. However, modern applications in statistics, engineering, and machine learning are posing problems with potentially tens of thousands of parameters or more. We revisit this convex programming problem and propose an algorithm that scales well with dimensionality. Our proposal is an instance of a sequential unconstrained minimization technique and revolves around three ideas: the majorization-minimization (MM) principle, the classical penalty method for constrained optimization, and quasi-Newton acceleration of fixed-point algorithms. The performance of our distance majorization algorithms is illustrated in several applications.