Towards Tuning-Free Minimum-Volume Nonnegative Matrix Factorization

Nonnegative Matrix Factorization (NMF) is a versatile and powerful tool for discovering latent structures in data matrices, with many variations proposed in the literature. Recently, Leplat et al.\@ (2019) introduced a minimum-volume NMF for the identifiable recovery of rank-deficient matrices in the presence of noise. The performance of their formulation, however, requires the selection of a tuning parameter whose optimal value depends on the unknown noise level. In this work, we propose an alternative formulation of minimum-volume NMF inspired by the square-root lasso and its tuning-free properties. Our formulation also requires the selection of a tuning parameter, but its optimal value does not depend on the noise level. To fit our NMF model, we propose a majorization-minimization (MM) algorithm that comes with global convergence guarantees. We show empirically that the optimal choice of our tuning parameter is insensitive to the noise level in the data.

A Majorization-Minimization Gauss-Newton Method for 1-Bit Matrix Completion

In 1-bit matrix completion, the aim is to estimate an underlying low-rank matrix from a partial set of binary observations. We propose a novel method for 1-bit matrix completion called MMGN. Our method is based on the majorization-minimization (MM) principle, which yields a sequence of standard low-rank matrix completion problems in our setting. We solve each of these sub-problems by a factorization approach that explicitly enforces the assumed low-rank structure and then apply a Gauss-Newton method. Our numerical studies and application to a real-data example illustrate that MMGN outputs comparable if not more accurate estimates, is often significantly faster, and is less sensitive to the spikiness of the underlying matrix than existing methods.

Multi-way Graph Signal Processing on Tensors: Integrative analysis of irregular geometries

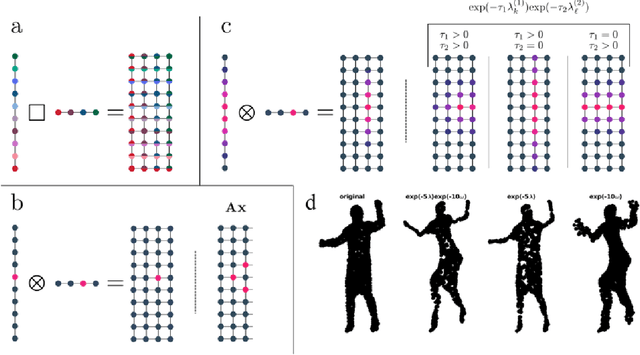
Graph signal processing (GSP) is an important methodology for studying arbitrarily structured data. As acquired data is increasingly taking the form of multi-way tensors, new signal processing tools are needed to maximally utilize the multi-way structure within the data. We review modern signal processing frameworks generalizing GSP to multi-way data, starting from graph signals coupled to familiar regular axes such as time in sensor networks, and then extending to general graphs across all tensor modes. This widely applicable paradigm motivates reformulating and improving upon classical problems and approaches to creatively address the challenges in tensor-based data. We synthesize common themes arising from current efforts to combine GSP with tensor analysis and highlight future directions in extending GSP to the multi-way paradigm.

Co-manifold learning with missing data

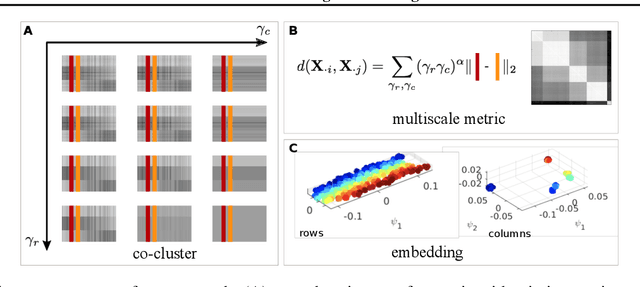
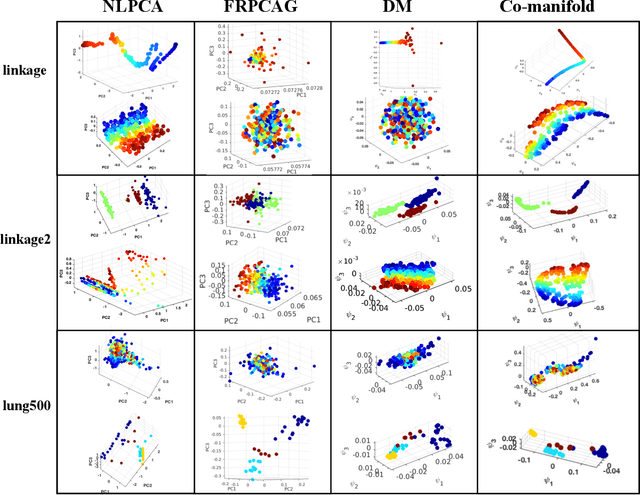
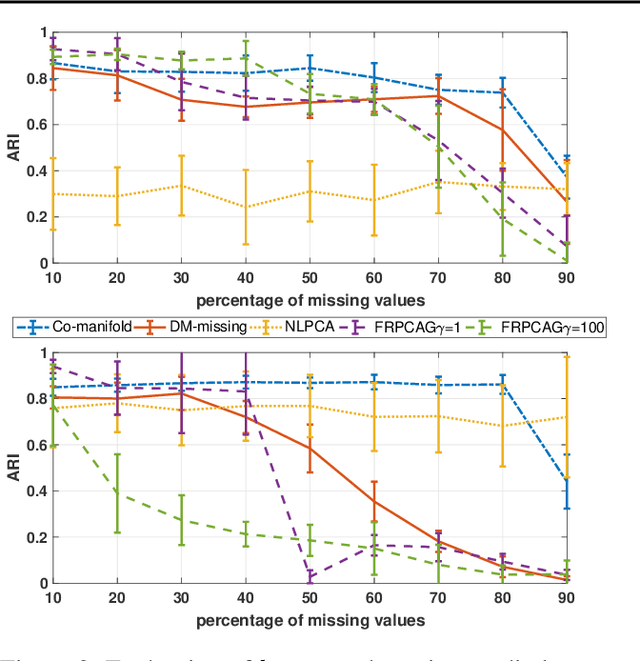
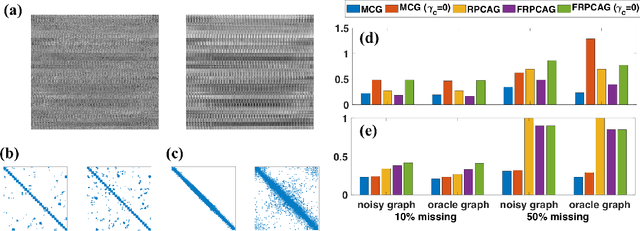
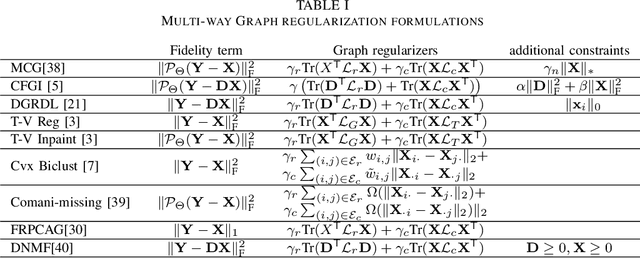
Representation learning is typically applied to only one mode of a data matrix, either its rows or columns. Yet in many applications, there is an underlying geometry to both the rows and the columns. We propose utilizing this coupled structure to perform co-manifold learning: uncovering the underlying geometry of both the rows and the columns of a given matrix, where we focus on a missing data setting. Our unsupervised approach consists of three components. We first solve a family of optimization problems to estimate a complete matrix at multiple scales of smoothness. We then use this collection of smooth matrix estimates to compute pairwise distances on the rows and columns based on a new multi-scale metric that implicitly introduces a coupling between the rows and the columns. Finally, we construct row and column representations from these multi-scale metrics. We demonstrate that our approach outperforms competing methods in both data visualization and clustering.

Recovering Trees with Convex Clustering

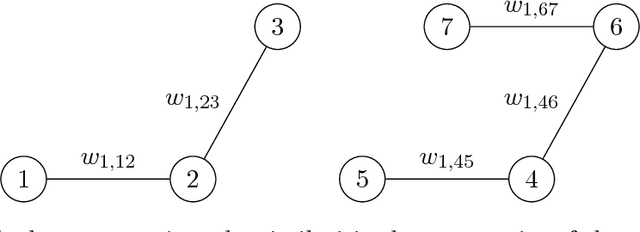
Convex clustering refers, for given $\left\{x_1, \dots, x_n\right\} \subset \mathbb{R}^p$, to the minimization of \begin{eqnarray*} u(\gamma) & = & \underset{u_1, \dots, u_n }{\arg\min}\;\sum_{i=1}^{n}{\lVert x_i - u_i \rVert^2} + \gamma \sum_{i,j=1}^{n}{w_{ij} \lVert u_i - u_j\rVert},\\ \end{eqnarray*} where $w_{ij} \geq 0$ is an affinity that quantifies the similarity between $x_i$ and $x_j$. We prove that if the affinities $w_{ij}$ reflect a tree structure in the $\left\{x_1, \dots, x_n\right\}$, then the convex clustering solution path reconstructs the tree exactly. The main technical ingredient implies the following combinatorial byproduct: for every set $\left\{x_1, \dots, x_n \right\} \subset \mathbb{R}^p$ of $n \geq 2$ distinct points, there exist at least $n/6$ points with the property that for any of these points $x$ there is a unit vector $v \in \mathbb{R}^p$ such that, when viewed from $x$, `most' points lie in the direction $v$ \begin{eqnarray*} \frac{1}{n-1}\sum_{i=1 \atop x_i \neq x}^{n}{ \left\langle \frac{x_i - x}{\lVert x_i - x \rVert}, v \right\rangle} & \geq & \frac{1}{4}. \end{eqnarray*}

Provable Convex Co-clustering of Tensors

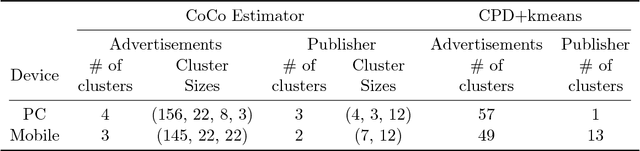
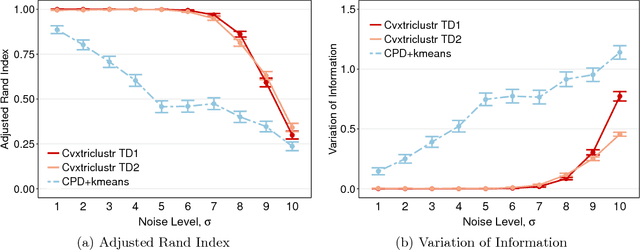
Cluster analysis is a fundamental tool for pattern discovery of complex heterogeneous data. Prevalent clustering methods mainly focus on vector or matrix-variate data and are not applicable to general-order tensors, which arise frequently in modern scientific and business applications. Moreover, there is a gap between statistical guarantees and computational efficiency for existing tensor clustering solutions due to the nature of their non-convex formulations. In this work, we bridge this gap by developing a provable convex formulation of tensor co-clustering. Our convex co-clustering (CoCo) estimator enjoys stability guarantees and is both computationally and storage efficient. We further establish a non-asymptotic error bound for the CoCo estimator, which reveals a surprising "blessing of dimensionality" phenomenon that does not exist in vector or matrix-variate cluster analysis. Our theoretical findings are supported by extensive simulated studies. Finally, we apply the CoCo estimator to the cluster analysis of advertisement click tensor data from a major online company. Our clustering results provide meaningful business insights to improve advertising effectiveness.

Generalized Linear Model Regression under Distance-to-set Penalties

Estimation in generalized linear models (GLM) is complicated by the presence of constraints. One can handle constraints by maximizing a penalized log-likelihood. Penalties such as the lasso are effective in high dimensions, but often lead to unwanted shrinkage. This paper explores instead penalizing the squared distance to constraint sets. Distance penalties are more flexible than algebraic and regularization penalties, and avoid the drawback of shrinkage. To optimize distance penalized objectives, we make use of the majorization-minimization principle. Resulting algorithms constructed within this framework are amenable to acceleration and come with global convergence guarantees. Applications to shape constraints, sparse regression, and rank-restricted matrix regression on synthetic and real data showcase strong empirical performance, even under non-convex constraints.

An MM Algorithm for Split Feasibility Problems

The classical multi-set split feasibility problem seeks a point in the intersection of finitely many closed convex domain constraints, whose image under a linear mapping also lies in the intersection of finitely many closed convex range constraints. Split feasibility generalizes important inverse problems including convex feasibility, linear complementarity, and regression with constraint sets. When a feasible point does not exist, solution methods that proceed by minimizing a proximity function can be used to obtain optimal approximate solutions to the problem. We present an extension of the proximity function approach that generalizes the linear split feasibility problem to allow for non-linear mappings. Our algorithm is based on the principle of majorization-minimization, is amenable to quasi-Newton acceleration, and comes complete with convergence guarantees under mild assumptions. Furthermore, we show that the Euclidean norm appearing in the proximity function of the non-linear split feasibility problem can be replaced by arbitrary Bregman divergences. We explore several examples illustrating the merits of non-linear formulations over the linear case, with a focus on optimization for intensity-modulated radiation therapy.

Shape Constrained Tensor Decompositions using Sparse Representations in Over-Complete Libraries

We consider $N$-way data arrays and low-rank tensor factorizations where the time mode is coded as a sparse linear combination of temporal elements from an over-complete library. Our method, Shape Constrained Tensor Decomposition (SCTD) is based upon the CANDECOMP/PARAFAC (CP) decomposition which produces $r$-rank approximations of data tensors via outer products of vectors in each dimension of the data. By constraining the vector in the temporal dimension to known analytic forms which are selected from a large set of candidate functions, more readily interpretable decompositions are achieved and analytic time dependencies discovered. The SCTD method circumvents traditional {\em flattening} techniques where an $N$-way array is reshaped into a matrix in order to perform a singular value decomposition. A clear advantage of the SCTD algorithm is its ability to extract transient and intermittent phenomena which is often difficult for SVD-based methods. We motivate the SCTD method using several intuitively appealing results before applying it on a number of high-dimensional, real-world data sets in order to illustrate the efficiency of the algorithm in extracting interpretable spatio-temporal modes. With the rise of data-driven discovery methods, the decomposition proposed provides a viable technique for analyzing multitudes of data in a more comprehensible fashion.

Convex Biclustering

In the biclustering problem, we seek to simultaneously group observations and features. While biclustering has applications in a wide array of domains, ranging from text mining to collaborative filtering, the problem of identifying structure in high dimensional genomic data motivates this work. In this context, biclustering enables us to identify subsets of genes that are co-expressed only within a subset of experimental conditions. We present a convex formulation of the biclustering problem that possesses a unique global minimizer and an iterative algorithm, COBRA, that is guaranteed to identify it. Our approach generates an entire solution path of possible biclusters as a single tuning parameter is varied. We also show how to reduce the problem of selecting this tuning parameter to solving a trivial modification of the convex biclustering problem. The key contributions of our work are its simplicity, interpretability, and algorithmic guarantees - features that arguably are lacking in the current alternative algorithms. We demonstrate the advantages of our approach, which includes stably and reproducibly identifying biclusterings, on simulated and real microarray data.