Multi-way Graph Signal Processing on Tensors: Integrative analysis of irregular geometries

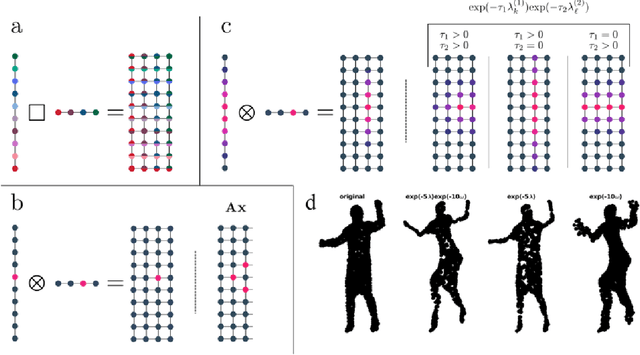
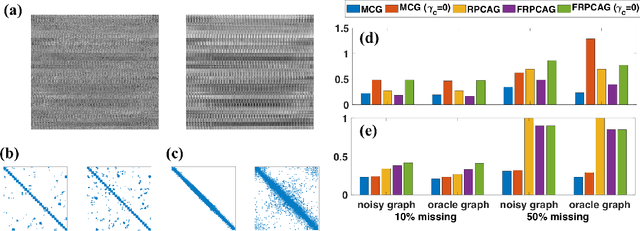
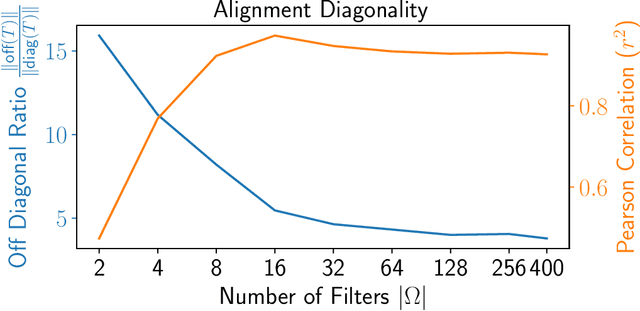
Graph signal processing (GSP) is an important methodology for studying arbitrarily structured data. As acquired data is increasingly taking the form of multi-way tensors, new signal processing tools are needed to maximally utilize the multi-way structure within the data. We review modern signal processing frameworks generalizing GSP to multi-way data, starting from graph signals coupled to familiar regular axes such as time in sensor networks, and then extending to general graphs across all tensor modes. This widely applicable paradigm motivates reformulating and improving upon classical problems and approaches to creatively address the challenges in tensor-based data. We synthesize common themes arising from current efforts to combine GSP with tensor analysis and highlight future directions in extending GSP to the multi-way paradigm.

Compressed Diffusion

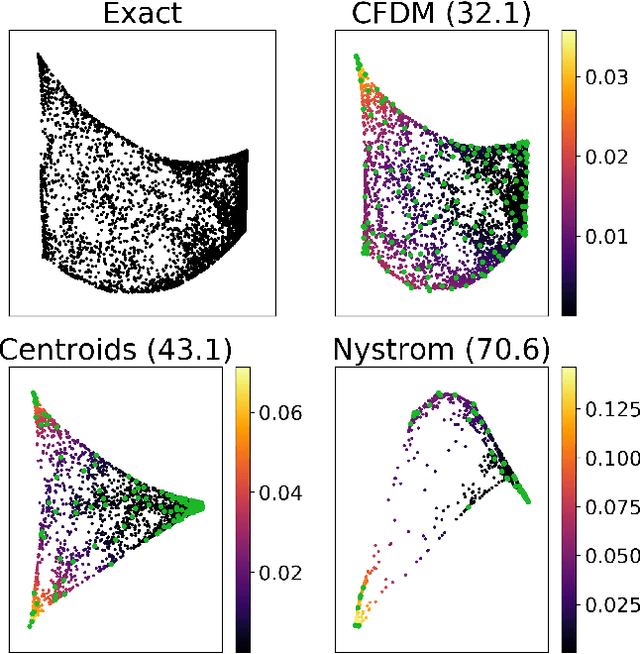
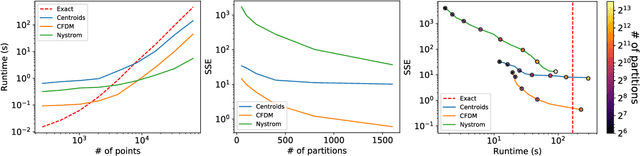
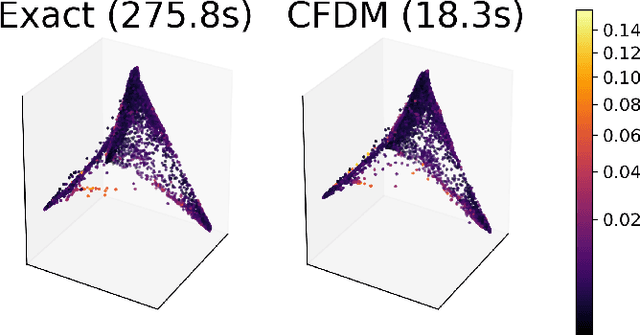
Diffusion maps are a commonly used kernel-based method for manifold learning, which can reveal intrinsic structures in data and embed them in low dimensions. However, as with most kernel methods, its implementation requires a heavy computational load, reaching up to cubic complexity in the number of data points. This limits its usability in modern data analysis. Here, we present a new approach to computing the diffusion geometry, and related embeddings, from a compressed diffusion process between data regions rather than data points. Our construction is based on an adaptation of the previously proposed measure-based (MGC) kernel that robustly captures the local geometry around data points. We use this MGC kernel to efficiently compress diffusion relations from pointwise to data region resolution. Finally, a spectral embedding of the data regions provides coordinates that are used to interpolate and approximate the pointwise diffusion map embedding of data. We analyze theoretical connections between our construction and the original diffusion geometry of diffusion maps, and demonstrate the utility of our method in analyzing big datasets, where it outperforms competing approaches.

Graph Spectral Regularization for Neural Network Interpretability

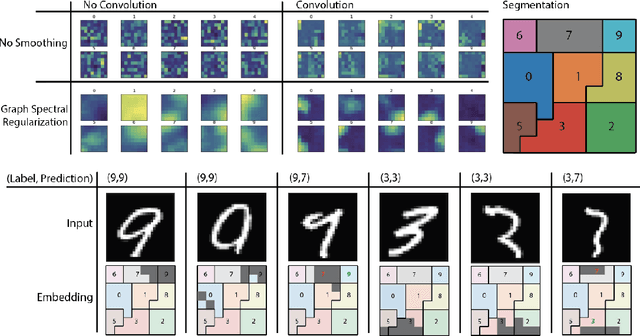
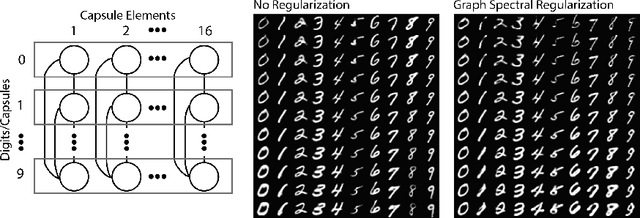
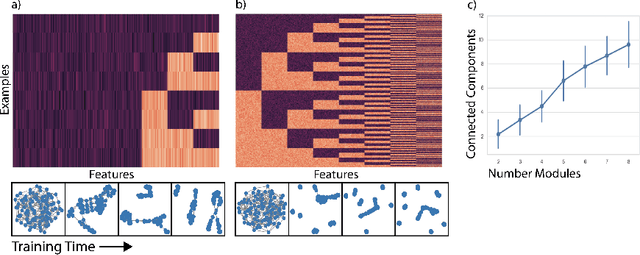
Deep neural networks can learn meaningful representations of data. However, these representations are hard to interpret. For example, visualizing a latent layer is generally only possible for at most three dimensions. Neural networks are able to learn and benefit from much higher dimensional representationsm but these are not visually interpretable because neurons have arbitrary ordering within a layer. Here, we utilize the ability of a human observer to identify patterns in structured representations to visualize higher dimensions. To do so, we propose a class of regularizations we call Graph Spectral Regularizations that impose graph structure on latent layers. This is achieved by treating activations as signals on a predefined graph and constraining those activations using graph filters, such as low pass and wavelet-like filters. This framework allows for any kind of graphs and filters to achieve a wide range of structured regularizations depending on the inference needs of the data. First, we show a synthetic example where a graph-structured layer reveals topological features of the data. Next, we show that a smoothing regularization imposes semantically consistent ordering of nodes when applied to capsule nets. Further, we show that the graph-structured layer, using wavelet-like spatially localized filters, can form local receptive fields for improved image and biomedical data interpretation. In other words, the mapping between latent layer, neurons and the output space becomes clear due to the localization of the activations. Finally, we show that when structured as a grid, the representations create coherent images that allow for image processing techniques such as convolutions.

Manifold Alignment with Feature Correspondence

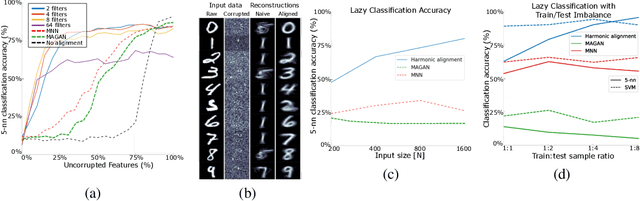
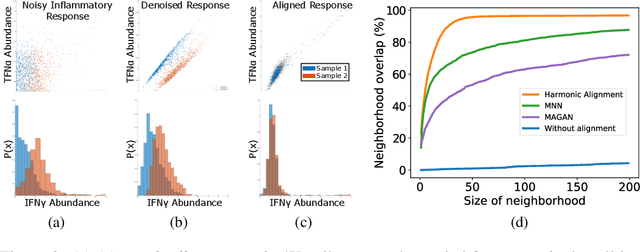
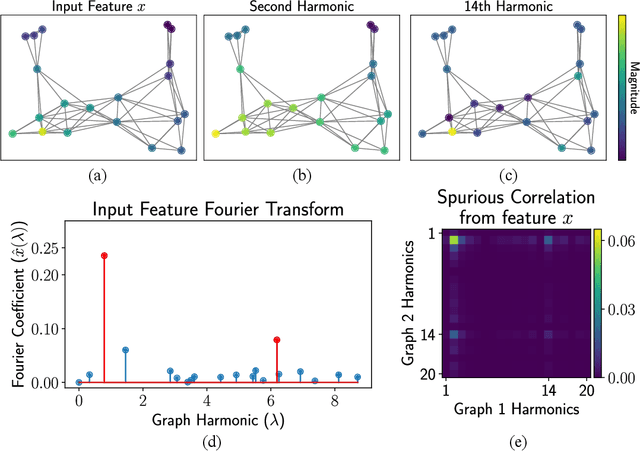
We propose a novel framework for combining datasets via alignment of their associated intrinsic dimensions. Our approach assumes that two datasets are sampled from a common latent space, i.e., they measure equivalent systems. Thus, we expect there to exist a natural (albeit unknown) alignment of the data manifolds associated with the intrinsic geometry of these datasets, which are perturbed by measurement artifacts in the sampling process. Importantly, we do not assume any individual correspondence (partial or complete) between data points. Instead, we rely on our assumption that a subset of data features have correspondence across datasets. We leverage this assumption to estimate relations between intrinsic manifold dimensions, which are given by diffusion map coordinates over each of the datasets. We compute a correlation matrix between diffusion coordinates of the datasets by considering graph (or manifold) Fourier coefficients of corresponding data features. We then orthogonalize this correlation matrix to form an isometric transformation between the diffusion maps of the datasets. Finally, we apply this transformation to the diffusion coordinates and construct a unified diffusion geometry of the datasets together. We show that this approach successfully corrects misalignment artifacts and enables data integration.

Geometry-Based Data Generation

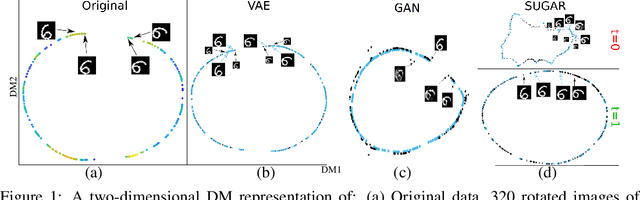
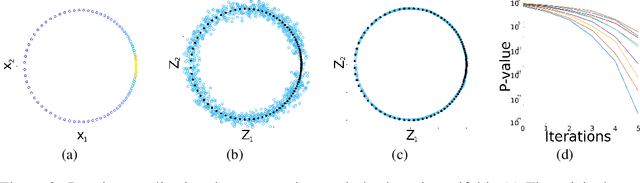
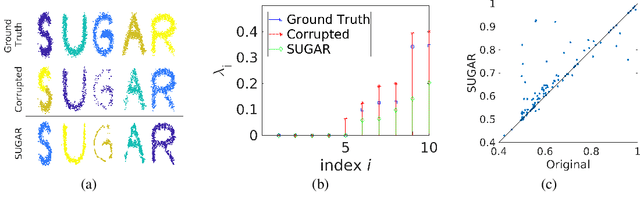
Many generative models attempt to replicate the density of their input data. However, this approach is often undesirable, since data density is highly affected by sampling biases, noise, and artifacts. We propose a method called SUGAR (Synthesis Using Geometrically Aligned Random-walks) that uses a diffusion process to learn a manifold geometry from the data. Then, it generates new points evenly along the manifold by pulling randomly generated points into its intrinsic structure using a diffusion kernel. SUGAR equalizes the density along the manifold by selectively generating points in sparse areas of the manifold. We demonstrate how the approach corrects sampling biases and artifacts, while also revealing intrinsic patterns (e.g. progression) and relations in the data. The method is applicable for correcting missing data, finding hypothetical data points, and learning relationships between data features.