Graph Spectral Regularization for Neural Network Interpretability

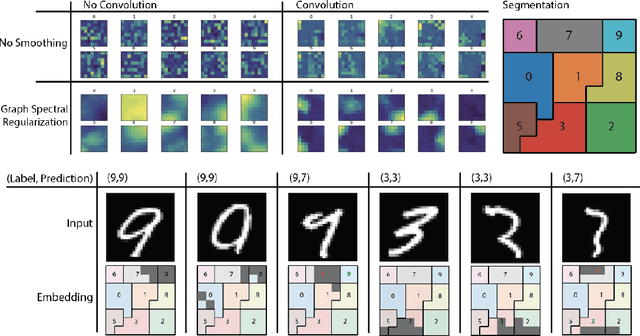
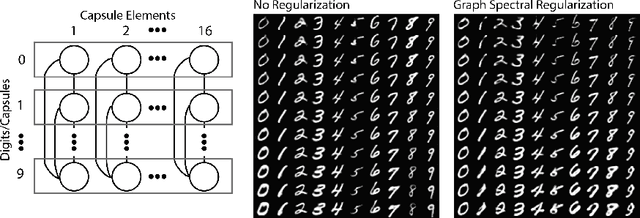
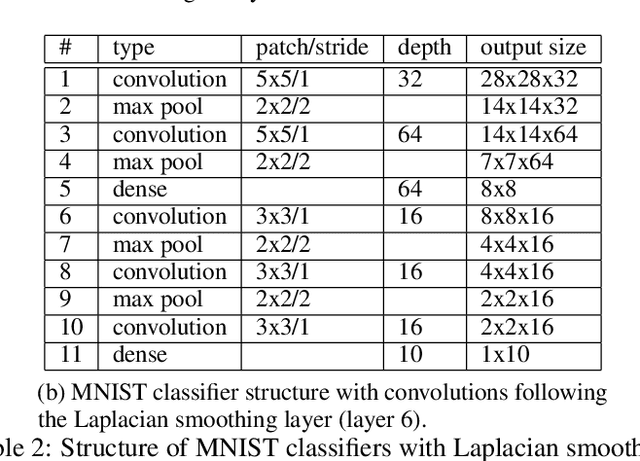
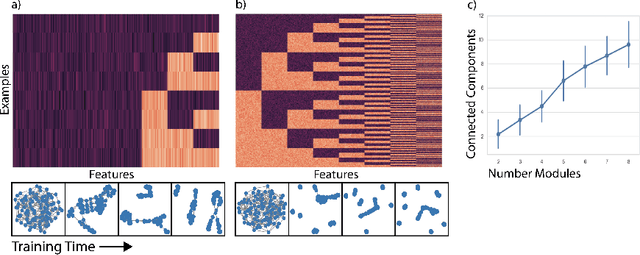
Deep neural networks can learn meaningful representations of data. However, these representations are hard to interpret. For example, visualizing a latent layer is generally only possible for at most three dimensions. Neural networks are able to learn and benefit from much higher dimensional representationsm but these are not visually interpretable because neurons have arbitrary ordering within a layer. Here, we utilize the ability of a human observer to identify patterns in structured representations to visualize higher dimensions. To do so, we propose a class of regularizations we call Graph Spectral Regularizations that impose graph structure on latent layers. This is achieved by treating activations as signals on a predefined graph and constraining those activations using graph filters, such as low pass and wavelet-like filters. This framework allows for any kind of graphs and filters to achieve a wide range of structured regularizations depending on the inference needs of the data. First, we show a synthetic example where a graph-structured layer reveals topological features of the data. Next, we show that a smoothing regularization imposes semantically consistent ordering of nodes when applied to capsule nets. Further, we show that the graph-structured layer, using wavelet-like spatially localized filters, can form local receptive fields for improved image and biomedical data interpretation. In other words, the mapping between latent layer, neurons and the output space becomes clear due to the localization of the activations. Finally, we show that when structured as a grid, the representations create coherent images that allow for image processing techniques such as convolutions.