COAST: Intelligent Time-Adaptive Neural Operators

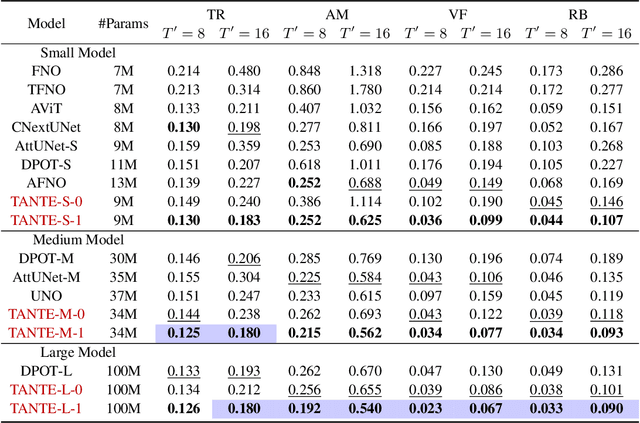
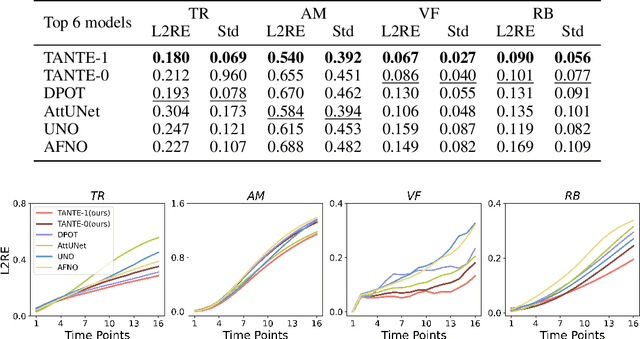
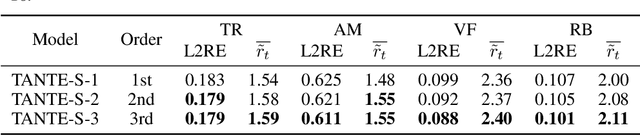
We introduce Causal Operator with Adaptive Solver Transformer (COAST), a novel neural operator learning method that leverages a causal language model (CLM) framework to dynamically adapt time steps. Our method predicts both the evolution of a system and its optimal time step, intelligently balancing computational efficiency and accuracy. We find that COAST generates variable step sizes that correlate with the underlying system intrinsicities, both within and across dynamical systems. Within a single trajectory, smaller steps are taken in regions of high complexity, while larger steps are employed in simpler regions. Across different systems, more complex dynamics receive more granular time steps. Benchmarked on diverse systems with varied dynamics, COAST consistently outperforms state-of-the-art methods, achieving superior performance in both efficiency and accuracy. This work underscores the potential of CLM-based intelligent adaptive solvers for scalable operator learning of dynamical systems.

Intelligence at the Edge of Chaos

We explore the emergence of intelligent behavior in artificial systems by investigating how the complexity of rule-based systems influences the capabilities of models trained to predict these rules. Our study focuses on elementary cellular automata (ECA), simple yet powerful one-dimensional systems that generate behaviors ranging from trivial to highly complex. By training distinct Large Language Models (LLMs) on different ECAs, we evaluated the relationship between the complexity of the rules' behavior and the intelligence exhibited by the LLMs, as reflected in their performance on downstream tasks. Our findings reveal that rules with higher complexity lead to models exhibiting greater intelligence, as demonstrated by their performance on reasoning and chess move prediction tasks. Both uniform and periodic systems, and often also highly chaotic systems, resulted in poorer downstream performance, highlighting a sweet spot of complexity conducive to intelligence. We conjecture that intelligence arises from the ability to predict complexity and that creating intelligence may require only exposure to complexity.

CaLMFlow: Volterra Flow Matching using Causal Language Models

We introduce CaLMFlow (Causal Language Models for Flow Matching), a novel framework that casts flow matching as a Volterra integral equation (VIE), leveraging the power of large language models (LLMs) for continuous data generation. CaLMFlow enables the direct application of LLMs to learn complex flows by formulating flow matching as a sequence modeling task, bridging discrete language modeling and continuous generative modeling. Our method implements tokenization across space and time, thereby solving a VIE over these domains. This approach enables efficient handling of high-dimensional data and outperforms ODE solver-dependent methods like conditional flow matching (CFM). We demonstrate CaLMFlow's effectiveness on synthetic and real-world data, including single-cell perturbation response prediction, showcasing its ability to incorporate textual context and generalize to unseen conditions. Our results highlight LLM-driven flow matching as a promising paradigm in generative modeling, offering improved scalability, flexibility, and context-awareness.

Operator Learning Meets Numerical Analysis: Improving Neural Networks through Iterative Methods

Deep neural networks, despite their success in numerous applications, often function without established theoretical foundations. In this paper, we bridge this gap by drawing parallels between deep learning and classical numerical analysis. By framing neural networks as operators with fixed points representing desired solutions, we develop a theoretical framework grounded in iterative methods for operator equations. Under defined conditions, we present convergence proofs based on fixed point theory. We demonstrate that popular architectures, such as diffusion models and AlphaFold, inherently employ iterative operator learning. Empirical assessments highlight that performing iterations through network operators improves performance. We also introduce an iterative graph neural network, PIGN, that further demonstrates benefits of iterations. Our work aims to enhance the understanding of deep learning by merging insights from numerical analysis, potentially guiding the design of future networks with clearer theoretical underpinnings and improved performance.

Continuous Spatiotemporal Transformers

Modeling spatiotemporal dynamical systems is a fundamental challenge in machine learning. Transformer models have been very successful in NLP and computer vision where they provide interpretable representations of data. However, a limitation of transformers in modeling continuous dynamical systems is that they are fundamentally discrete time and space models and thus have no guarantees regarding continuous sampling. To address this challenge, we present the Continuous Spatiotemporal Transformer (CST), a new transformer architecture that is designed for the modeling of continuous systems. This new framework guarantees a continuous and smooth output via optimization in Sobolev space. We benchmark CST against traditional transformers as well as other spatiotemporal dynamics modeling methods and achieve superior performance in a number of tasks on synthetic and real systems, including learning brain dynamics from calcium imaging data.

AMPNet: Attention as Message Passing for Graph Neural Networks

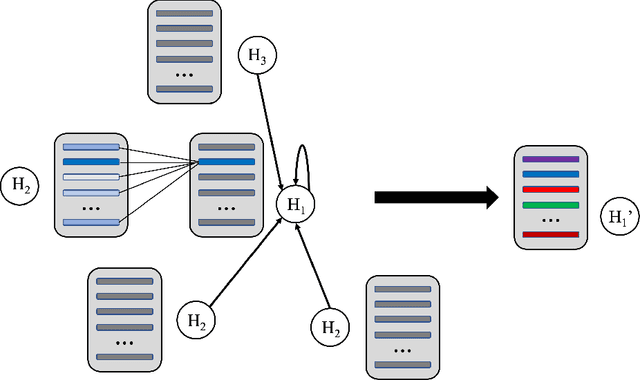
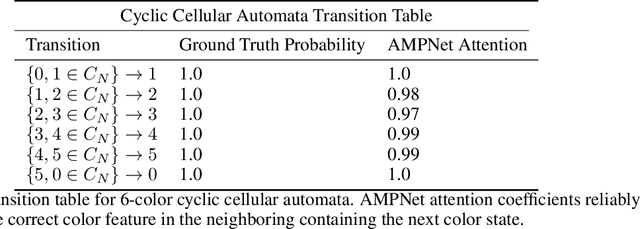
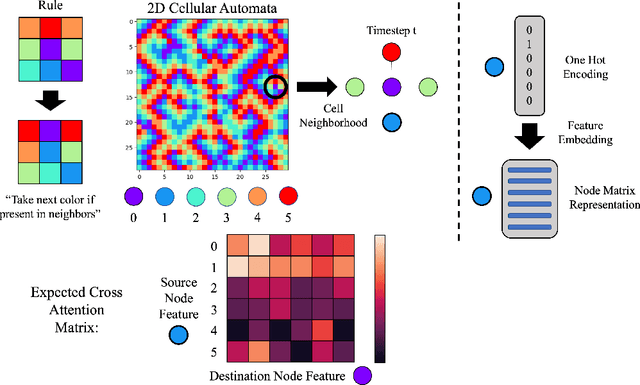
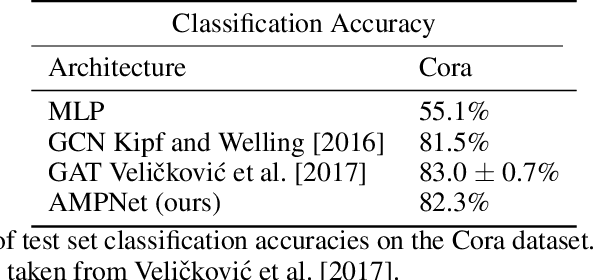
Feature-level interactions between nodes can carry crucial information for understanding complex interactions in graph-structured data. Current interpretability techniques, however, are limited in their ability to capture feature-level interactions between different nodes. In this work, we propose AMPNet, a general Graph Neural Network (GNN) architecture for uncovering feature-level interactions between different spatial locations within graph-structured data. Our framework applies a multiheaded attention operation during message-passing to contextualize messages based on the feature interactions between different nodes. We evaluate AMPNet on several benchmark and real-world datasets, and develop a synthetic benchmark based on cyclic cellular automata to test the ability of our framework to recover cyclic patterns in node states based on feature-interactions. We also propose several methods for addressing the scalability of our architecture to large graphs, including subgraph sampling during training and node feature downsampling.

Neural Integral Equations

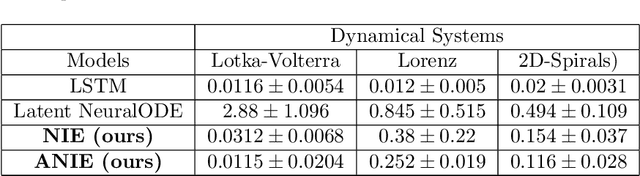
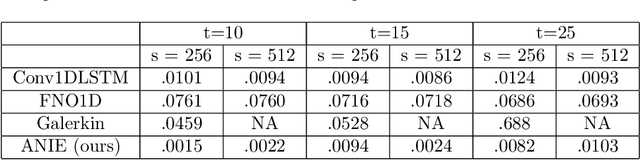
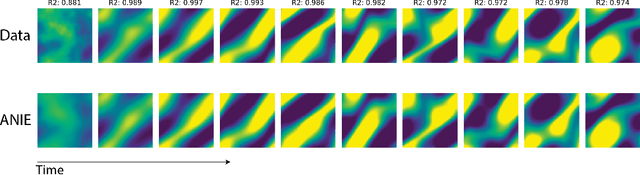
Integral equations (IEs) are functional equations defined through integral operators, where the unknown function is integrated over a possibly multidimensional space. Important applications of IEs have been found throughout theoretical and applied sciences, including in physics, chemistry, biology, and engineering; often in the form of inverse problems. IEs are especially useful since differential equations, e.g. ordinary differential equations (ODEs), and partial differential equations (PDEs) can be formulated in an integral version which is often more convenient to solve. Moreover, unlike ODEs and PDEs, IEs can model inherently non-local dynamical systems, such as ones with long distance spatiotemporal relations. While efficient algorithms exist for solving given IEs, no method exists that can learn an integral equation and its associated dynamics from data alone. In this article, we introduce Neural Integral Equations (NIE), a method that learns an unknown integral operator from data through a solver. We also introduce an attentional version of NIE, called Attentional Neural Integral Equations (ANIE), where the integral is replaced by self-attention, which improves scalability and provides interpretability. We show that learning dynamics via integral equations is faster than doing so via other continuous methods, such as Neural ODEs. Finally, we show that ANIE outperforms other methods on several benchmark tasks in ODE, PDE, and IE systems of synthetic and real-world data.

Neural Integro-Differential Equations

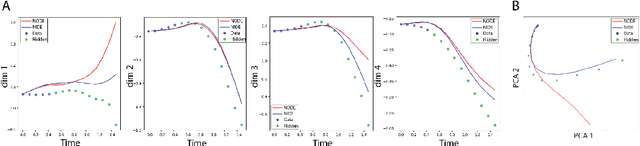
Modeling continuous dynamical systems from discretely sampled observations is a fundamental problem in data science. Often, such dynamics are the result of non-local processes that present an integral over time. As such, these systems are modeled with Integro-Differential Equations (IDEs); generalizations of differential equations that comprise both an integral and a differential component. For example, brain dynamics are not accurately modeled by differential equations since their behavior is non-Markovian, i.e. dynamics are in part dictated by history. Here, we introduce the Neural IDE (NIDE), a framework that models ordinary and integral components of IDEs using neural networks. We test NIDE on several toy and brain activity datasets and demonstrate that NIDE outperforms other models, including Neural ODE. These tasks include time extrapolation as well as predicting dynamics from unseen initial conditions, which we test on whole-cortex activity recordings in freely behaving mice. Further, we show that NIDE can decompose dynamics into its Markovian and non-Markovian constituents, via the learned integral operator, which we test on fMRI brain activity recordings of people on ketamine. Finally, the integrand of the integral operator provides a latent space that gives insight into the underlying dynamics, which we demonstrate on wide-field brain imaging recordings. Altogether, NIDE is a novel approach that enables modeling of complex non-local dynamics with neural networks.

Permutation invariant networks to learn Wasserstein metrics

Understanding the space of probability measures on a metric space equipped with a Wasserstein distance is one of the fundamental questions in mathematical analysis. The Wasserstein metric has received a lot of attention in the machine learning community especially for its principled way of comparing distributions. In this work, we use a permutation invariant network to map samples from probability measures into a low-dimensional space such that the Euclidean distance between the encoded samples reflects the Wasserstein distance between probability measures. We show that our network can generalize to correctly compute distances between unseen densities. We also show that these networks can learn the first and the second moments of probability distributions.

Self-supervised edge features for improved Graph Neural Network training

Graph Neural Networks (GNN) have been extensively used to extract meaningful representations from graph structured data and to perform predictive tasks such as node classification and link prediction. In recent years, there has been a lot of work incorporating edge features along with node features for prediction tasks. One of the main difficulties in using edge features is that they are often handcrafted, hard to get, specific to a particular domain, and may contain redundant information. In this work, we present a framework for creating new edge features, applicable to any domain, via a combination of self-supervised and unsupervised learning. In addition to this, we use Forman-Ricci curvature as an additional edge feature to encapsulate the local geometry of the graph. We then encode our edge features via a Set Transformer and combine them with node features extracted from popular GNN architectures for node classification in an end-to-end training scheme. We validate our work on three biological datasets comprising of single-cell RNA sequencing data of neurological disease, \textit{in vitro} SARS-CoV-2 infection, and human COVID-19 patients. We demonstrate that our method achieves better performance on node classification tasks over baseline Graph Attention Network (GAT) and Graph Convolutional Network (GCN) models. Furthermore, given the attention mechanism on edge and node features, we are able to interpret the cell types and genes that determine the course and severity of COVID-19, contributing to a growing list of potential disease biomarkers and therapeutic targets.