Antonio Henrique de Oliveira Fonseca
Neural Integral Equations
Oct 12, 2022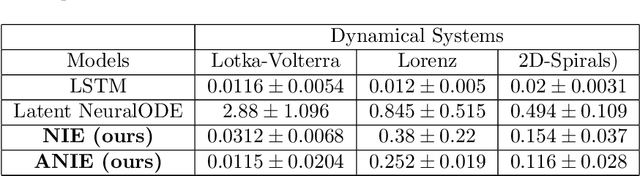

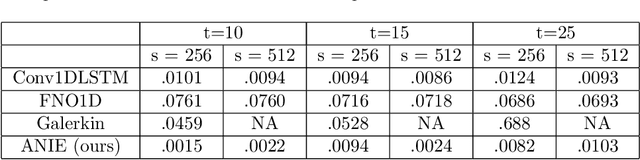
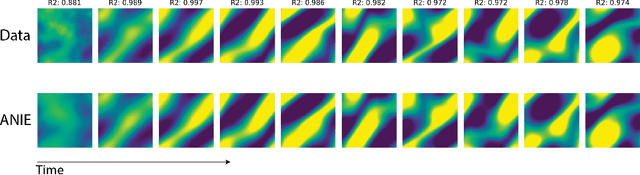
Abstract:Integral equations (IEs) are functional equations defined through integral operators, where the unknown function is integrated over a possibly multidimensional space. Important applications of IEs have been found throughout theoretical and applied sciences, including in physics, chemistry, biology, and engineering; often in the form of inverse problems. IEs are especially useful since differential equations, e.g. ordinary differential equations (ODEs), and partial differential equations (PDEs) can be formulated in an integral version which is often more convenient to solve. Moreover, unlike ODEs and PDEs, IEs can model inherently non-local dynamical systems, such as ones with long distance spatiotemporal relations. While efficient algorithms exist for solving given IEs, no method exists that can learn an integral equation and its associated dynamics from data alone. In this article, we introduce Neural Integral Equations (NIE), a method that learns an unknown integral operator from data through a solver. We also introduce an attentional version of NIE, called Attentional Neural Integral Equations (ANIE), where the integral is replaced by self-attention, which improves scalability and provides interpretability. We show that learning dynamics via integral equations is faster than doing so via other continuous methods, such as Neural ODEs. Finally, we show that ANIE outperforms other methods on several benchmark tasks in ODE, PDE, and IE systems of synthetic and real-world data.
Neural Integro-Differential Equations
Jun 28, 2022


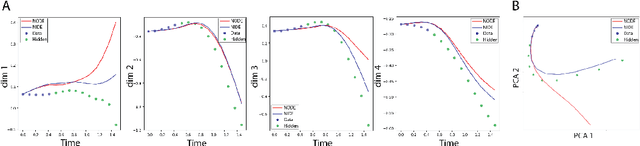
Abstract:Modeling continuous dynamical systems from discretely sampled observations is a fundamental problem in data science. Often, such dynamics are the result of non-local processes that present an integral over time. As such, these systems are modeled with Integro-Differential Equations (IDEs); generalizations of differential equations that comprise both an integral and a differential component. For example, brain dynamics are not accurately modeled by differential equations since their behavior is non-Markovian, i.e. dynamics are in part dictated by history. Here, we introduce the Neural IDE (NIDE), a framework that models ordinary and integral components of IDEs using neural networks. We test NIDE on several toy and brain activity datasets and demonstrate that NIDE outperforms other models, including Neural ODE. These tasks include time extrapolation as well as predicting dynamics from unseen initial conditions, which we test on whole-cortex activity recordings in freely behaving mice. Further, we show that NIDE can decompose dynamics into its Markovian and non-Markovian constituents, via the learned integral operator, which we test on fMRI brain activity recordings of people on ketamine. Finally, the integrand of the integral operator provides a latent space that gives insight into the underlying dynamics, which we demonstrate on wide-field brain imaging recordings. Altogether, NIDE is a novel approach that enables modeling of complex non-local dynamics with neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge