Neural Integral Equations
Paper and Code
Oct 12, 2022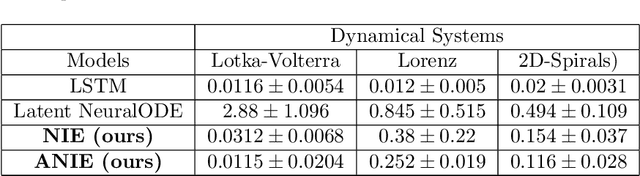

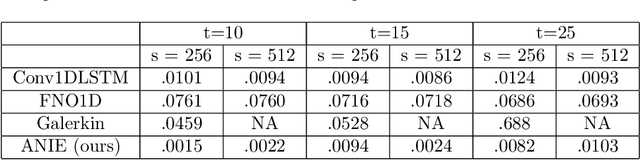
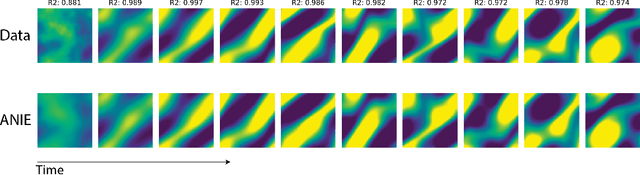
Integral equations (IEs) are functional equations defined through integral operators, where the unknown function is integrated over a possibly multidimensional space. Important applications of IEs have been found throughout theoretical and applied sciences, including in physics, chemistry, biology, and engineering; often in the form of inverse problems. IEs are especially useful since differential equations, e.g. ordinary differential equations (ODEs), and partial differential equations (PDEs) can be formulated in an integral version which is often more convenient to solve. Moreover, unlike ODEs and PDEs, IEs can model inherently non-local dynamical systems, such as ones with long distance spatiotemporal relations. While efficient algorithms exist for solving given IEs, no method exists that can learn an integral equation and its associated dynamics from data alone. In this article, we introduce Neural Integral Equations (NIE), a method that learns an unknown integral operator from data through a solver. We also introduce an attentional version of NIE, called Attentional Neural Integral Equations (ANIE), where the integral is replaced by self-attention, which improves scalability and provides interpretability. We show that learning dynamics via integral equations is faster than doing so via other continuous methods, such as Neural ODEs. Finally, we show that ANIE outperforms other methods on several benchmark tasks in ODE, PDE, and IE systems of synthetic and real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge