CaLMFlow: Volterra Flow Matching using Causal Language Models

We introduce CaLMFlow (Causal Language Models for Flow Matching), a novel framework that casts flow matching as a Volterra integral equation (VIE), leveraging the power of large language models (LLMs) for continuous data generation. CaLMFlow enables the direct application of LLMs to learn complex flows by formulating flow matching as a sequence modeling task, bridging discrete language modeling and continuous generative modeling. Our method implements tokenization across space and time, thereby solving a VIE over these domains. This approach enables efficient handling of high-dimensional data and outperforms ODE solver-dependent methods like conditional flow matching (CFM). We demonstrate CaLMFlow's effectiveness on synthetic and real-world data, including single-cell perturbation response prediction, showcasing its ability to incorporate textual context and generalize to unseen conditions. Our results highlight LLM-driven flow matching as a promising paradigm in generative modeling, offering improved scalability, flexibility, and context-awareness.

Intelligence at the Edge of Chaos

We explore the emergence of intelligent behavior in artificial systems by investigating how the complexity of rule-based systems influences the capabilities of models trained to predict these rules. Our study focuses on elementary cellular automata (ECA), simple yet powerful one-dimensional systems that generate behaviors ranging from trivial to highly complex. By training distinct Large Language Models (LLMs) on different ECAs, we evaluated the relationship between the complexity of the rules' behavior and the intelligence exhibited by the LLMs, as reflected in their performance on downstream tasks. Our findings reveal that rules with higher complexity lead to models exhibiting greater intelligence, as demonstrated by their performance on reasoning and chess move prediction tasks. Both uniform and periodic systems, and often also highly chaotic systems, resulted in poorer downstream performance, highlighting a sweet spot of complexity conducive to intelligence. We conjecture that intelligence arises from the ability to predict complexity and that creating intelligence may require only exposure to complexity.

Leray-Schauder Mappings for Operator Learning

We present an algorithm for learning operators between Banach spaces, based on the use of Leray-Schauder mappings to learn a finite-dimensional approximation of compact subspaces. We show that the resulting method is a universal approximator of (possibly nonlinear) operators. We demonstrate the efficiency of the approach on two benchmark datasets showing it achieves results comparable to state of the art models.

Universal Approximation of Operators with Transformers and Neural Integral Operators

We study the universal approximation properties of transformers and neural integral operators for operators in Banach spaces. In particular, we show that the transformer architecture is a universal approximator of integral operators between H\"older spaces. Moreover, we show that a generalized version of neural integral operators, based on the Gavurin integral, are universal approximators of arbitrary operators between Banach spaces. Lastly, we show that a modified version of transformer, which uses Leray-Schauder mappings, is a universal approximator of operators between arbitrary Banach spaces.

Projection Methods for Operator Learning and Universal Approximation

We obtain a new universal approximation theorem for continuous operators on arbitrary Banach spaces using the Leray-Schauder mapping. Moreover, we introduce and study a method for operator learning in Banach spaces $L^p$ of functions with multiple variables, based on orthogonal projections on polynomial bases. We derive a universal approximation result for operators where we learn a linear projection and a finite dimensional mapping under some additional assumptions. For the case of $p=2$, we give some sufficient conditions for the approximation results to hold. This article serves as the theoretical framework for a deep learning methodology whose implementation will be provided in subsequent work.

Spectral methods for Neural Integral Equations

Neural integral equations are deep learning models based on the theory of integral equations, where the model consists of an integral operator and the corresponding equation (of the second kind) which is learned through an optimization procedure. This approach allows to leverage the nonlocal properties of integral operators in machine learning, but it is computationally expensive. In this article, we introduce a framework for neural integral equations based on spectral methods that allows us to learn an operator in the spectral domain, resulting in a cheaper computational cost, as well as in high interpolation accuracy. We study the properties of our methods and show various theoretical guarantees regarding the approximation capabilities of the model, and convergence to solutions of the numerical methods. We provide numerical experiments to demonstrate the practical effectiveness of the resulting model.

Operator Learning Meets Numerical Analysis: Improving Neural Networks through Iterative Methods

Deep neural networks, despite their success in numerous applications, often function without established theoretical foundations. In this paper, we bridge this gap by drawing parallels between deep learning and classical numerical analysis. By framing neural networks as operators with fixed points representing desired solutions, we develop a theoretical framework grounded in iterative methods for operator equations. Under defined conditions, we present convergence proofs based on fixed point theory. We demonstrate that popular architectures, such as diffusion models and AlphaFold, inherently employ iterative operator learning. Empirical assessments highlight that performing iterations through network operators improves performance. We also introduce an iterative graph neural network, PIGN, that further demonstrates benefits of iterations. Our work aims to enhance the understanding of deep learning by merging insights from numerical analysis, potentially guiding the design of future networks with clearer theoretical underpinnings and improved performance.

Continuous Spatiotemporal Transformers

Modeling spatiotemporal dynamical systems is a fundamental challenge in machine learning. Transformer models have been very successful in NLP and computer vision where they provide interpretable representations of data. However, a limitation of transformers in modeling continuous dynamical systems is that they are fundamentally discrete time and space models and thus have no guarantees regarding continuous sampling. To address this challenge, we present the Continuous Spatiotemporal Transformer (CST), a new transformer architecture that is designed for the modeling of continuous systems. This new framework guarantees a continuous and smooth output via optimization in Sobolev space. We benchmark CST against traditional transformers as well as other spatiotemporal dynamics modeling methods and achieve superior performance in a number of tasks on synthetic and real systems, including learning brain dynamics from calcium imaging data.

Deep Neural Networks as the Semi-classical Limit of Topological Quantum Neural Networks: The problem of generalisation

Deep Neural Networks miss a principled model of their operation. A novel framework for supervised learning based on Topological Quantum Field Theory that looks particularly well suited for implementation on quantum processors has been recently explored. We propose the use of this framework for understanding the problem of generalization in Deep Neural Networks. More specifically, in this approach Deep Neural Networks are viewed as the semi-classical limit of Topological Quantum Neural Networks. A framework of this kind explains easily the overfitting behavior of Deep Neural Networks during the training step and the corresponding generalization capabilities.

AMPNet: Attention as Message Passing for Graph Neural Networks

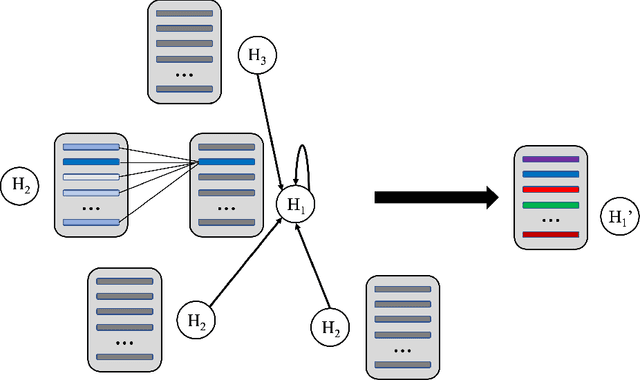
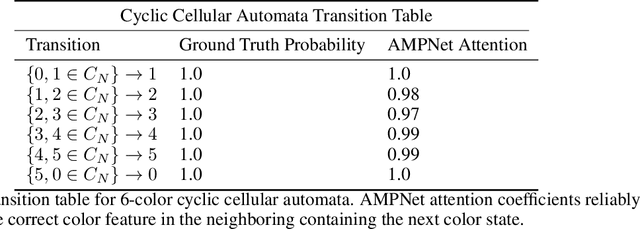
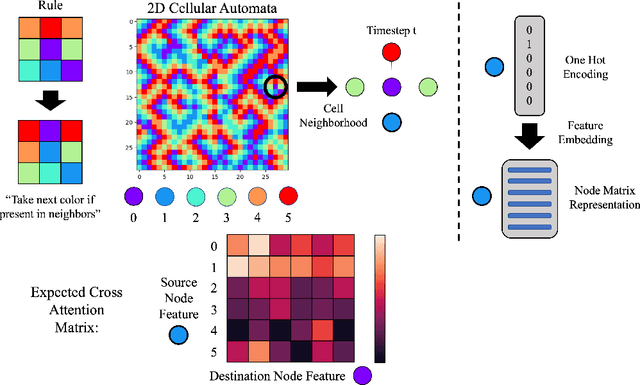
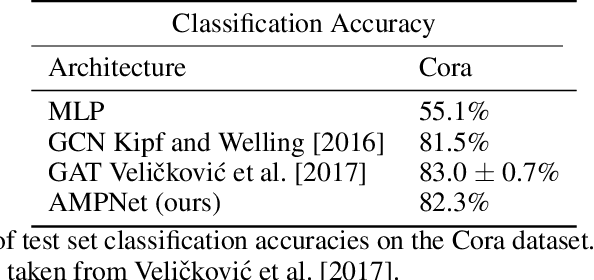
Feature-level interactions between nodes can carry crucial information for understanding complex interactions in graph-structured data. Current interpretability techniques, however, are limited in their ability to capture feature-level interactions between different nodes. In this work, we propose AMPNet, a general Graph Neural Network (GNN) architecture for uncovering feature-level interactions between different spatial locations within graph-structured data. Our framework applies a multiheaded attention operation during message-passing to contextualize messages based on the feature interactions between different nodes. We evaluate AMPNet on several benchmark and real-world datasets, and develop a synthetic benchmark based on cyclic cellular automata to test the ability of our framework to recover cyclic patterns in node states based on feature-interactions. We also propose several methods for addressing the scalability of our architecture to large graphs, including subgraph sampling during training and node feature downsampling.