Remapping and navigation of an embedding space via error minimization: a fundamental organizational principle of cognition in natural and artificial systems

The emerging field of diverse intelligence seeks an integrated view of problem-solving in agents of very different provenance, composition, and substrates. From subcellular chemical networks to swarms of organisms, and across evolved, engineered, and chimeric systems, it is hypothesized that scale-invariant principles of decision-making can be discovered. We propose that cognition in both natural and synthetic systems can be characterized and understood by the interplay between two equally important invariants: (1) the remapping of embedding spaces, and (2) the navigation within these spaces. Biological collectives, from single cells to entire organisms (and beyond), remap transcriptional, morphological, physiological, or 3D spaces to maintain homeostasis and regenerate structure, while navigating these spaces through distributed error correction. Modern Artificial Intelligence (AI) systems, including transformers, diffusion models, and neural cellular automata enact analogous processes by remapping data into latent embeddings and refining them iteratively through contextualization. We argue that this dual principle - remapping and navigation of embedding spaces via iterative error minimization - constitutes a substrate-independent invariant of cognition. Recognizing this shared mechanism not only illuminates deep parallels between living systems and artificial models, but also provides a unifying framework for engineering adaptive intelligence across scales.

Separability, Contextuality, and the Quantum Frame Problem

We study the relationship between assumptions of state separability and both preparation and measurement contextuality, and the relationship of both of these to the frame problem, the problem of predicting what does not change in consequence of an action. We state a quantum analog of the latter and prove its undecidability. We show how contextuality is generically induced in state preparation and measurement by basis choice, thermodynamic exchange, and the imposition of a priori causal models, and how fine-tuning assumptions appear ubiquitously in settings characterized as non-contextual.

Deep Neural Networks as the Semi-classical Limit of Topological Quantum Neural Networks: The problem of generalisation

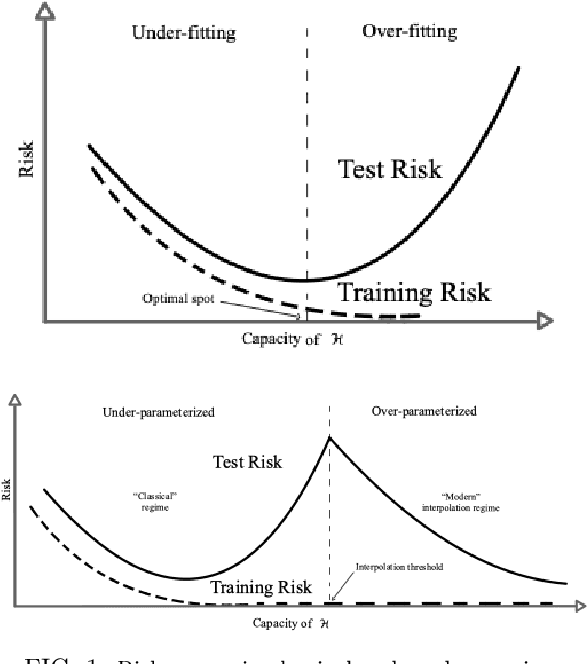
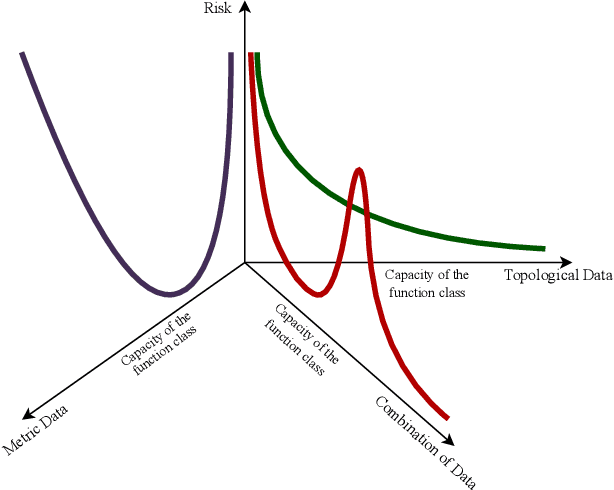
Deep Neural Networks miss a principled model of their operation. A novel framework for supervised learning based on Topological Quantum Field Theory that looks particularly well suited for implementation on quantum processors has been recently explored. We propose the use of this framework for understanding the problem of generalization in Deep Neural Networks. More specifically, in this approach Deep Neural Networks are viewed as the semi-classical limit of Topological Quantum Neural Networks. A framework of this kind explains easily the overfitting behavior of Deep Neural Networks during the training step and the corresponding generalization capabilities.

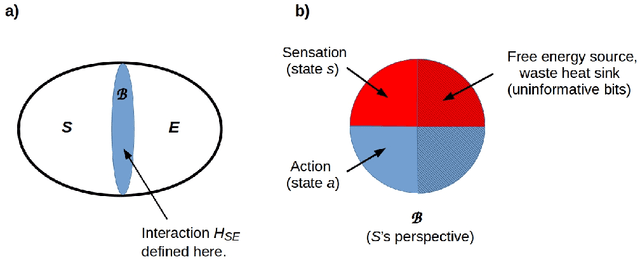
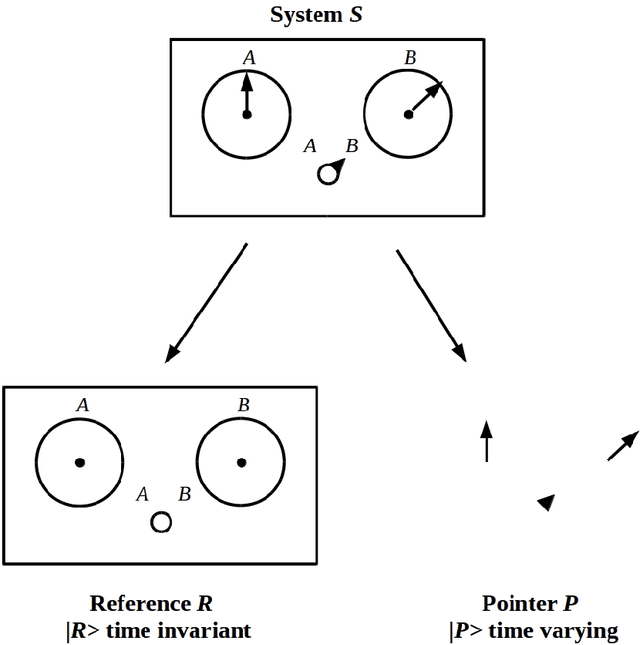
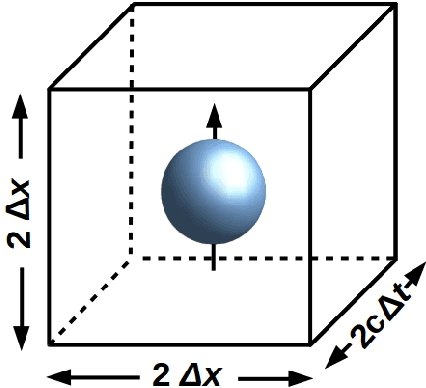
The Free Energy Principle drives neuromorphic development

We show how any system with morphological degrees of freedom and locally limited free energy will, under the constraints of the free energy principle, evolve toward a neuromorphic morphology that supports hierarchical computations in which each level of the hierarchy enacts a coarse-graining of its inputs, and dually a fine-graining of its outputs. Such hierarchies occur throughout biology, from the architectures of intracellular signal transduction pathways to the large-scale organization of perception and action cycles in the mammalian brain. Formally, the close formal connections between cone-cocone diagrams (CCCD) as models of quantum reference frames on the one hand, and between CCCDs and topological quantum field theories on the other, allow the representation of such computations in the fully-general quantum-computational framework of topological quantum neural networks.

A mosaic of Chu spaces and Channel Theory with applications to Object Identification and Mereological Complexity

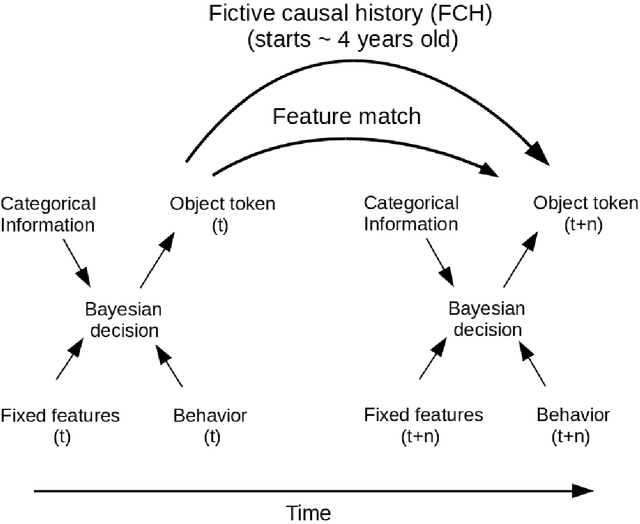
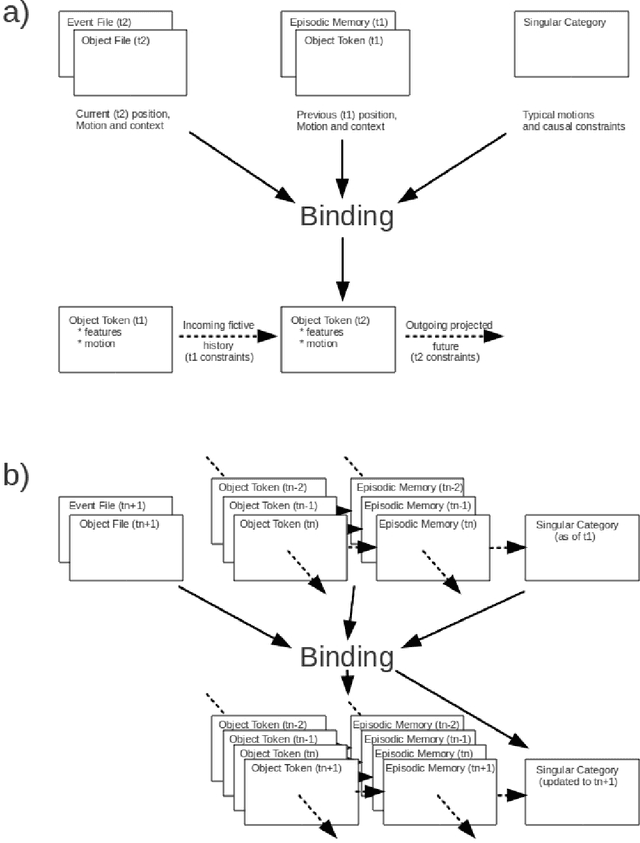
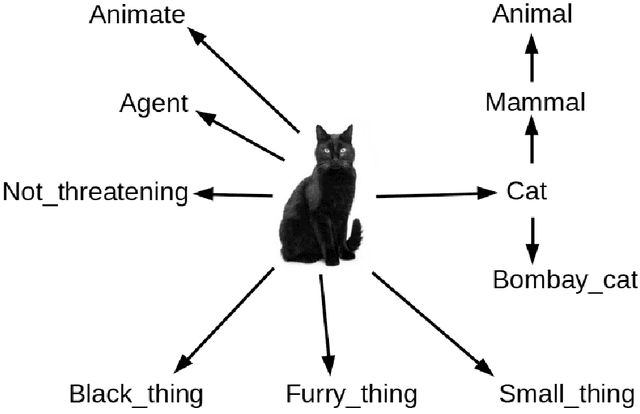
Chu Spaces and Channel Theory are well established areas of investigation in the general context of category theory. We review a range of examples and applications of these methods in logic and computer science, including Formal Concept Analysis, distributed systems and ontology development. We then employ these methods to describe human object perception, beginning with the construction of uncategorized object files and proceeding through categorization, individual object identification and the tracking of object identity through time. We investigate the relationship between abstraction and mereological categorization, particularly as these affect object identity tracking. This we accomplish in terms of information flow that is semantically structured in terms of local logics, while at the same time this framework also provides an inferential mechanism towards identification and perception. We show how a mereotopology naturally emerges from the representation of classifications by simplicial complexes, and briefly explore the emergence of geometric relations and interactions between objects.