Separability, Contextuality, and the Quantum Frame Problem

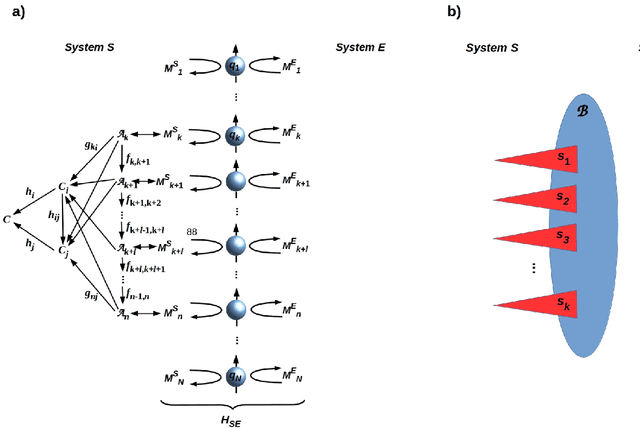
We study the relationship between assumptions of state separability and both preparation and measurement contextuality, and the relationship of both of these to the frame problem, the problem of predicting what does not change in consequence of an action. We state a quantum analog of the latter and prove its undecidability. We show how contextuality is generically induced in state preparation and measurement by basis choice, thermodynamic exchange, and the imposition of a priori causal models, and how fine-tuning assumptions appear ubiquitously in settings characterized as non-contextual.

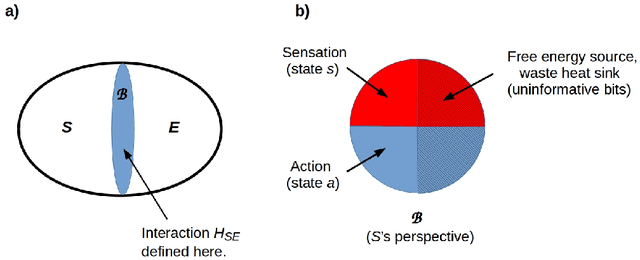
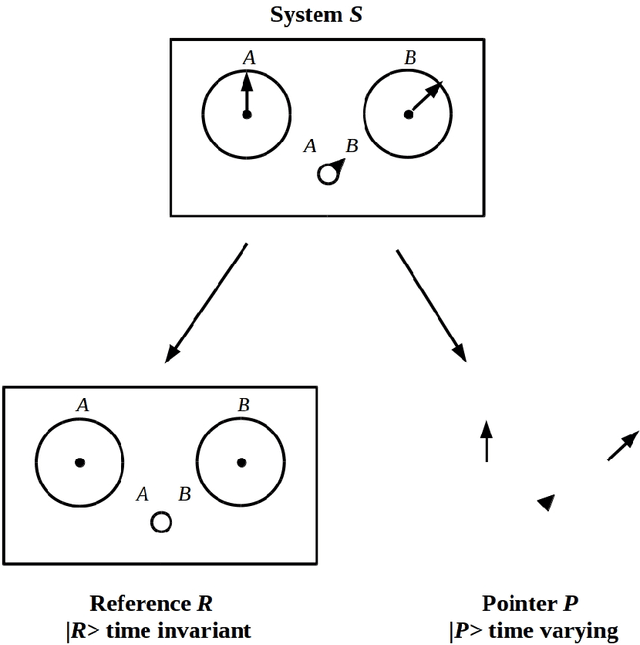
The Free Energy Principle drives neuromorphic development

We show how any system with morphological degrees of freedom and locally limited free energy will, under the constraints of the free energy principle, evolve toward a neuromorphic morphology that supports hierarchical computations in which each level of the hierarchy enacts a coarse-graining of its inputs, and dually a fine-graining of its outputs. Such hierarchies occur throughout biology, from the architectures of intracellular signal transduction pathways to the large-scale organization of perception and action cycles in the mammalian brain. Formally, the close formal connections between cone-cocone diagrams (CCCD) as models of quantum reference frames on the one hand, and between CCCDs and topological quantum field theories on the other, allow the representation of such computations in the fully-general quantum-computational framework of topological quantum neural networks.

A mosaic of Chu spaces and Channel Theory with applications to Object Identification and Mereological Complexity

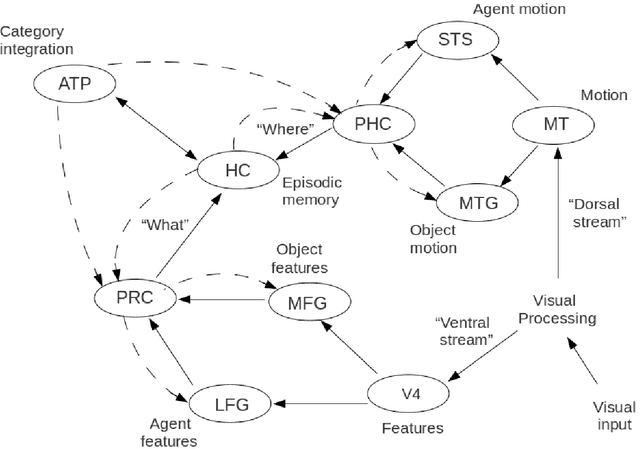
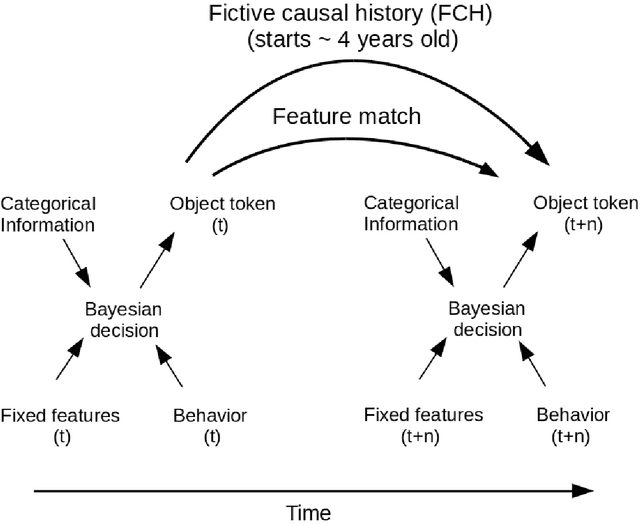
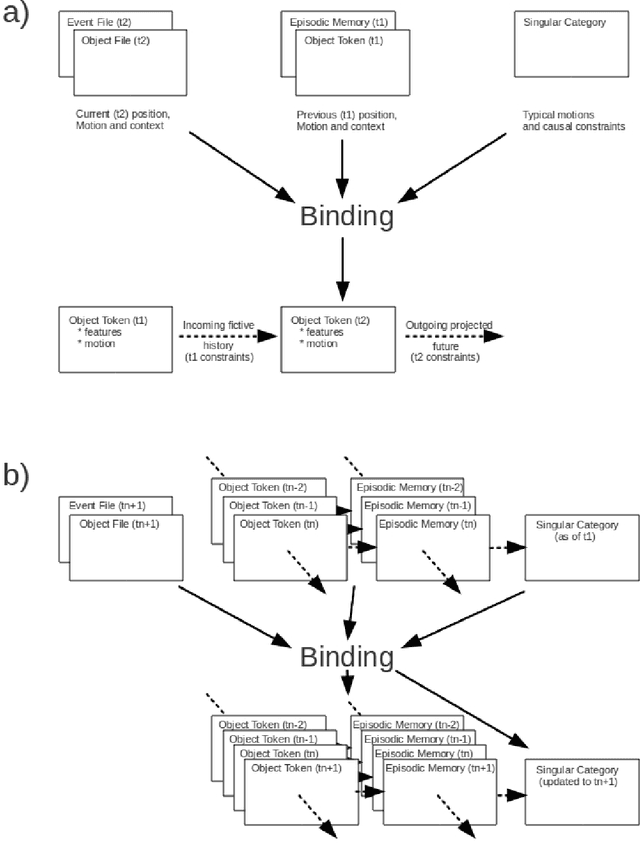
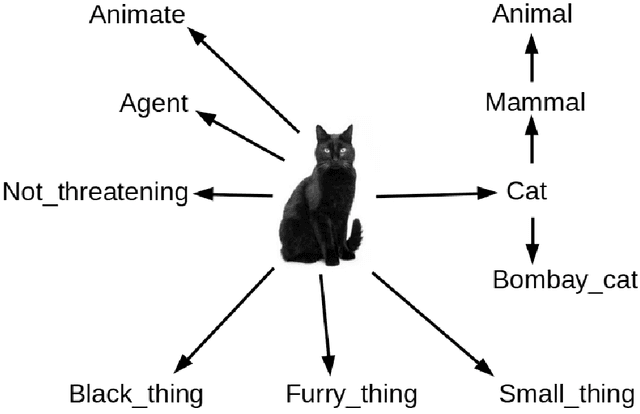
Chu Spaces and Channel Theory are well established areas of investigation in the general context of category theory. We review a range of examples and applications of these methods in logic and computer science, including Formal Concept Analysis, distributed systems and ontology development. We then employ these methods to describe human object perception, beginning with the construction of uncategorized object files and proceeding through categorization, individual object identification and the tracking of object identity through time. We investigate the relationship between abstraction and mereological categorization, particularly as these affect object identity tracking. This we accomplish in terms of information flow that is semantically structured in terms of local logics, while at the same time this framework also provides an inferential mechanism towards identification and perception. We show how a mereotopology naturally emerges from the representation of classifications by simplicial complexes, and briefly explore the emergence of geometric relations and interactions between objects.