Towards causally linking architectural parametrizations to algorithmic bias in neural networks

Training dataset biases are by far the most scrutinized factors when explaining algorithmic biases of neural networks. In contrast, hyperparameters related to the neural network architecture, e.g., the number of layers or choice of activation functions, have largely been ignored even though different network parameterizations are known to induce different implicit biases over learned features. For example, convolutional kernel size has been shown to bias CNNs towards different frequencies. In order to study the effect of these hyperparameters, we designed a causal framework for linking an architectural hyperparameter to algorithmic bias. Our framework is experimental, in that several versions of a network are trained with an intervention to a specific hyperparameter, and the resulting causal effect of this choice on performance bias is measured. We focused on the causal relationship between sensitivity to high-frequency image details and face analysis classification performance across different subpopulations (race/gender). In this work, we show that modifying a CNN hyperparameter (convolutional kernel size), even in one layer of a CNN, will not only change a fundamental characteristic of the learned features (frequency content) but that this change can vary significantly across data subgroups (race/gender populations) leading to biased generalization performance even in the presence of a balanced dataset.

Continuous Spatiotemporal Transformers

Modeling spatiotemporal dynamical systems is a fundamental challenge in machine learning. Transformer models have been very successful in NLP and computer vision where they provide interpretable representations of data. However, a limitation of transformers in modeling continuous dynamical systems is that they are fundamentally discrete time and space models and thus have no guarantees regarding continuous sampling. To address this challenge, we present the Continuous Spatiotemporal Transformer (CST), a new transformer architecture that is designed for the modeling of continuous systems. This new framework guarantees a continuous and smooth output via optimization in Sobolev space. We benchmark CST against traditional transformers as well as other spatiotemporal dynamics modeling methods and achieve superior performance in a number of tasks on synthetic and real systems, including learning brain dynamics from calcium imaging data.

AMPNet: Attention as Message Passing for Graph Neural Networks

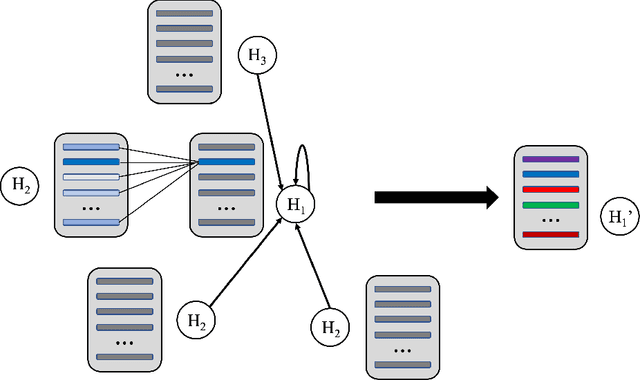
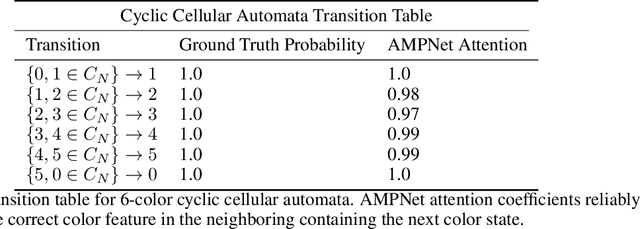
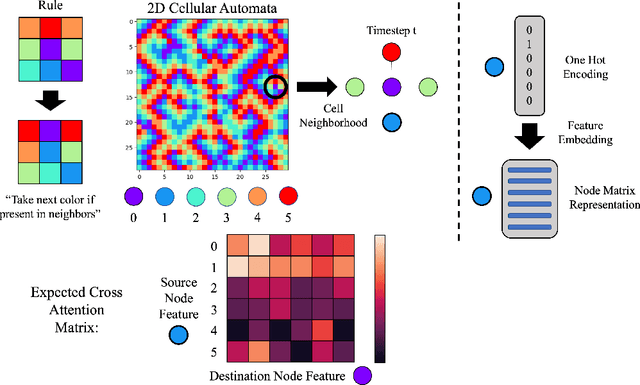
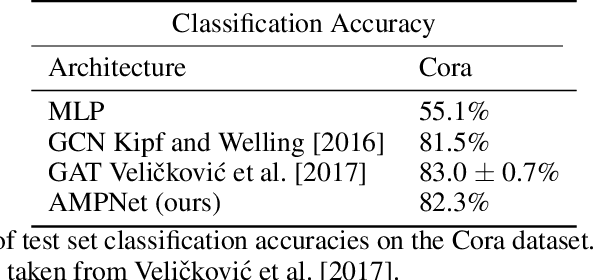
Feature-level interactions between nodes can carry crucial information for understanding complex interactions in graph-structured data. Current interpretability techniques, however, are limited in their ability to capture feature-level interactions between different nodes. In this work, we propose AMPNet, a general Graph Neural Network (GNN) architecture for uncovering feature-level interactions between different spatial locations within graph-structured data. Our framework applies a multiheaded attention operation during message-passing to contextualize messages based on the feature interactions between different nodes. We evaluate AMPNet on several benchmark and real-world datasets, and develop a synthetic benchmark based on cyclic cellular automata to test the ability of our framework to recover cyclic patterns in node states based on feature-interactions. We also propose several methods for addressing the scalability of our architecture to large graphs, including subgraph sampling during training and node feature downsampling.

Neural Integral Equations

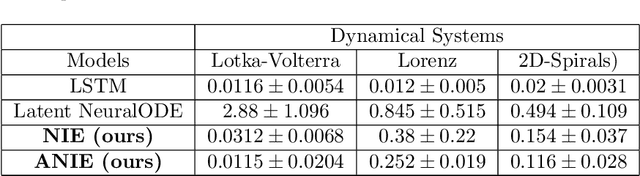
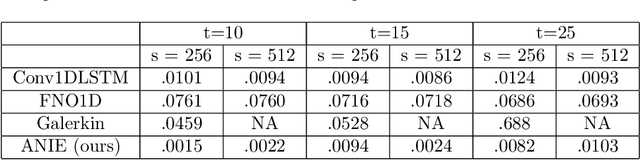
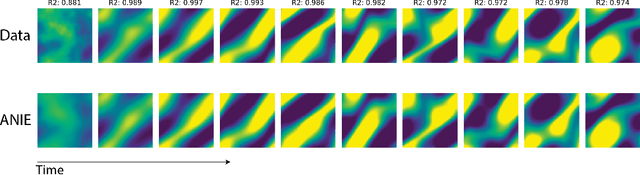
Integral equations (IEs) are functional equations defined through integral operators, where the unknown function is integrated over a possibly multidimensional space. Important applications of IEs have been found throughout theoretical and applied sciences, including in physics, chemistry, biology, and engineering; often in the form of inverse problems. IEs are especially useful since differential equations, e.g. ordinary differential equations (ODEs), and partial differential equations (PDEs) can be formulated in an integral version which is often more convenient to solve. Moreover, unlike ODEs and PDEs, IEs can model inherently non-local dynamical systems, such as ones with long distance spatiotemporal relations. While efficient algorithms exist for solving given IEs, no method exists that can learn an integral equation and its associated dynamics from data alone. In this article, we introduce Neural Integral Equations (NIE), a method that learns an unknown integral operator from data through a solver. We also introduce an attentional version of NIE, called Attentional Neural Integral Equations (ANIE), where the integral is replaced by self-attention, which improves scalability and provides interpretability. We show that learning dynamics via integral equations is faster than doing so via other continuous methods, such as Neural ODEs. Finally, we show that ANIE outperforms other methods on several benchmark tasks in ODE, PDE, and IE systems of synthetic and real-world data.

Understanding robustness and generalization of artificial neural networks through Fourier masks

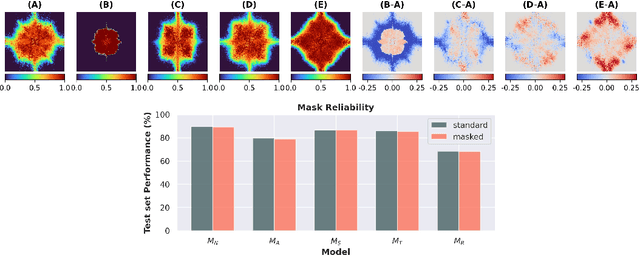
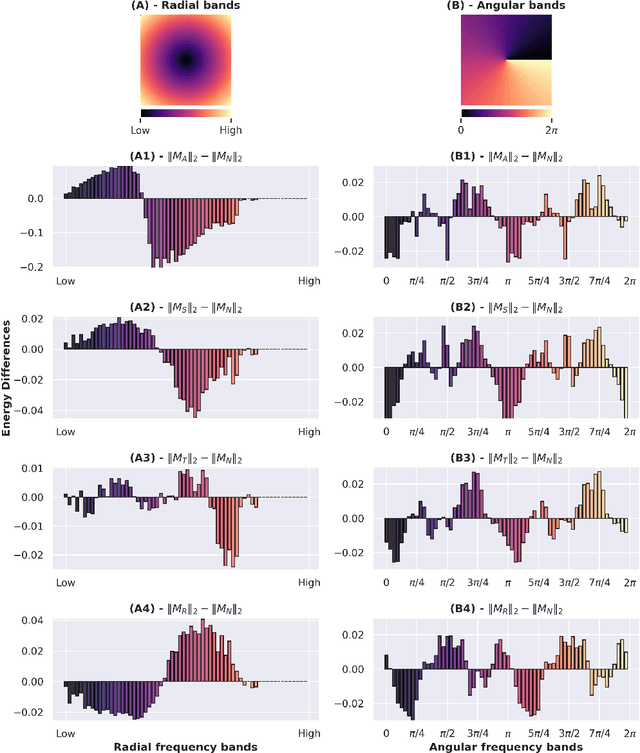
Despite the enormous success of artificial neural networks (ANNs) in many disciplines, the characterization of their computations and the origin of key properties such as generalization and robustness remain open questions. Recent literature suggests that robust networks with good generalization properties tend to be biased towards processing low frequencies in images. To explore the frequency bias hypothesis further, we develop an algorithm that allows us to learn modulatory masks highlighting the essential input frequencies needed for preserving a trained network's performance. We achieve this by imposing invariance in the loss with respect to such modulations in the input frequencies. We first use our method to test the low-frequency preference hypothesis of adversarially trained or data-augmented networks. Our results suggest that adversarially robust networks indeed exhibit a low-frequency bias but we find this bias is also dependent on directions in frequency space. However, this is not necessarily true for other types of data augmentation. Our results also indicate that the essential frequencies in question are effectively the ones used to achieve generalization in the first place. Surprisingly, images seen through these modulatory masks are not recognizable and resemble texture-like patterns.

Shallow Univariate ReLu Networks as Splines: Initialization, Loss Surface, Hessian, & Gradient Flow Dynamics

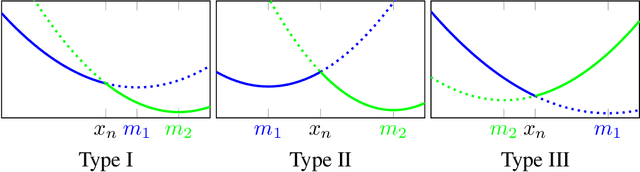
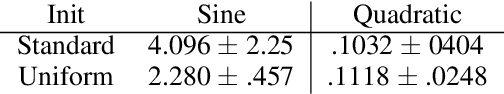
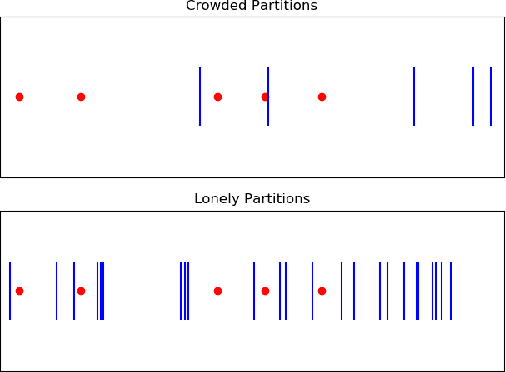
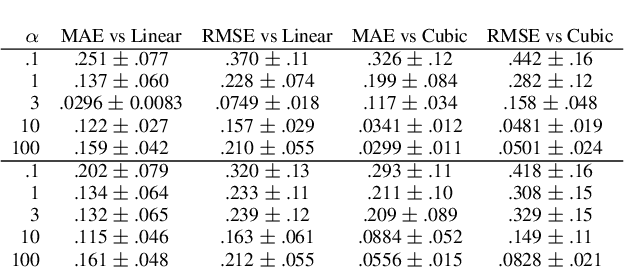
Understanding the learning dynamics and inductive bias of neural networks (NNs) is hindered by the opacity of the relationship between NN parameters and the function represented. We propose reparametrizing ReLU NNs as continuous piecewise linear splines. Using this spline lens, we study learning dynamics in shallow univariate ReLU NNs, finding unexpected insights and explanations for several perplexing phenomena. We develop a surprisingly simple and transparent view of the structure of the loss surface, including its critical and fixed points, Hessian, and Hessian spectrum. We also show that standard weight initializations yield very flat functions, and that this flatness, together with overparametrization and the initial weight scale, is responsible for the strength and type of implicit regularization, consistent with recent work arXiv:1906.05827. Our implicit regularization results are complementary to recent work arXiv:1906.07842, done independently, which showed that initialization scale critically controls implicit regularization via a kernel-based argument. Our spline-based approach reproduces their key implicit regularization results but in a far more intuitive and transparent manner. Going forward, our spline-based approach is likely to extend naturally to the multivariate and deep settings, and will play a foundational role in efforts to understand neural networks. Videos of learning dynamics using a spline-based visualization are available at http://shorturl.at/tFWZ2.

Using Learning Dynamics to Explore the Role of Implicit Regularization in Adversarial Examples

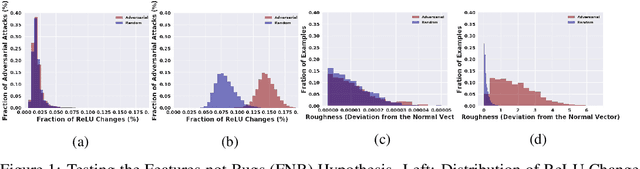
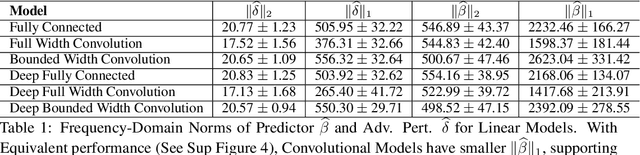
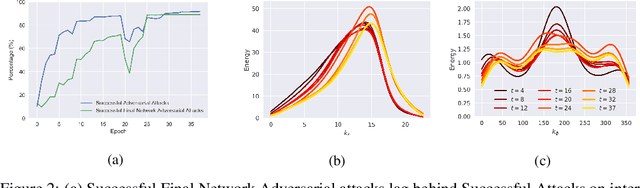
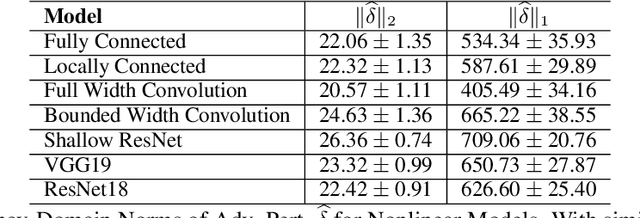
Recent work (Ilyas et al, 2019) suggests that adversarial examples are features not bugs. If adversarial perturbations are indeed useful but non-robust features, then what is their origin? In order to answer these questions, we systematically examine the learning dynamics of adversarial perturbations both in the pixel and frequency domains. We find that: (1) adversarial examples are not present at initialization but instead emerge very early in training, typically within the first epochs, as verified by a novel breakpoint-based analysis; (2) the low-amplitude high-frequency nature of common adversarial perturbations in natural images is critically dependent on an implicit bias towards sparsity in the frequency domain; and (3) the origin of this bias is the locality and translation invariance of convolutional filters, along with (4) the existence of useful frequency-domain features in natural images. We provide a simple theoretical explanation for these observations, providing a clear and minimalist target for theorists in future work. Looking forward, our findings suggest that analyzing the learning dynamics of perturbations can provide useful insights for understanding the origin of adversarial sensitivities and developing robust solutions.

Recurrent computations for visual pattern completion

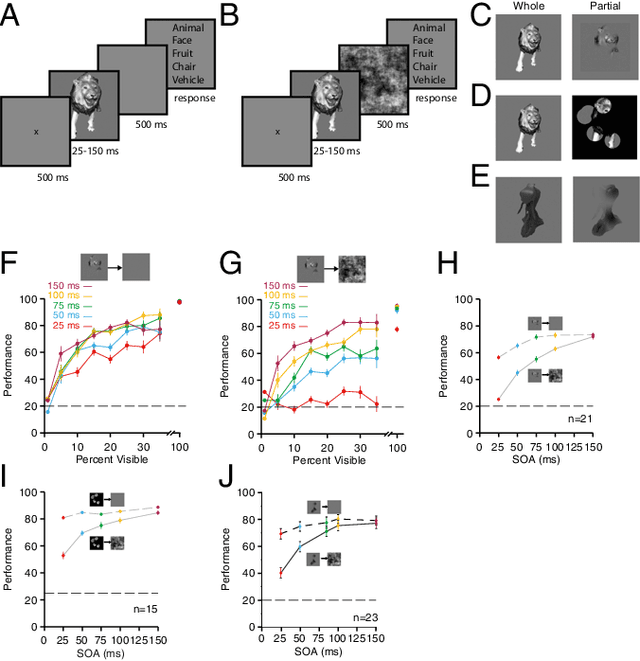
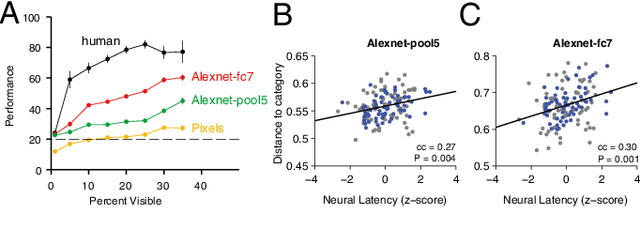
Making inferences from partial information constitutes a critical aspect of cognition. During visual perception, pattern completion enables recognition of poorly visible or occluded objects. We combined psychophysics, physiology and computational models to test the hypothesis that pattern completion is implemented by recurrent computations and present three pieces of evidence that are consistent with this hypothesis. First, subjects robustly recognized objects even when rendered <15% visible, but recognition was largely impaired when processing was interrupted by backward masking. Second, invasive physiological responses along the human ventral cortex exhibited visually selective responses to partially visible objects that were delayed compared to whole objects, suggesting the need for additional computations. These physiological delays were correlated with the effects of backward masking. Third, state-of-the-art feed-forward computational architectures were not robust to partial visibility. However, recognition performance was recovered when the model was augmented with attractor-based recurrent connectivity. These results provide a strong argument of plausibility for the role of recurrent computations in making visual inferences from partial information.