Intrinsic Dimension Correlation: uncovering nonlinear connections in multimodal representations

To gain insight into the mechanisms behind machine learning methods, it is crucial to establish connections among the features describing data points. However, these correlations often exhibit a high-dimensional and strongly nonlinear nature, which makes them challenging to detect using standard methods. This paper exploits the entanglement between intrinsic dimensionality and correlation to propose a metric that quantifies the (potentially nonlinear) correlation between high-dimensional manifolds. We first validate our method on synthetic data in controlled environments, showcasing its advantages and drawbacks compared to existing techniques. Subsequently, we extend our analysis to large-scale applications in neural network representations. Specifically, we focus on latent representations of multimodal data, uncovering clear correlations between paired visual and textual embeddings, whereas existing methods struggle significantly in detecting similarity. Our results indicate the presence of highly nonlinear correlation patterns between latent manifolds.

Local Search, Semantics, and Genetic Programming: a Global Analysis

Geometric Semantic Geometric Programming (GSGP) is one of the most prominent Genetic Programming (GP) variants, thanks to its solid theoretical background, the excellent performance achieved, and the execution time significantly smaller than standard syntax-based GP. In recent years, a new mutation operator, Geometric Semantic Mutation with Local Search (GSM-LS), has been proposed to include a local search step in the mutation process based on the idea that performing a linear regression during the mutation can allow for a faster convergence to good-quality solutions. While GSM-LS helps the convergence of the evolutionary search, it is prone to overfitting. Thus, it was suggested to use GSM-LS only for a limited number of generations and, subsequently, to switch back to standard geometric semantic mutation. A more recently defined variant of GSGP (called GSGP-reg) also includes a local search step but shares similar strengths and weaknesses with GSM-LS. Here we explore multiple possibilities to limit the overfitting of GSM-LS and GSGP-reg, ranging from adaptive methods to estimate the risk of overfitting at each mutation to a simple regularized regression. The results show that the method used to limit overfitting is not that important: providing that a technique to control overfitting is used, it is possible to consistently outperform standard GSGP on both training and unseen data. The obtained results allow practitioners to better understand the role of local search in GSGP and demonstrate that simple regularization strategies are effective in controlling overfitting.

Relating Implicit Bias and Adversarial Attacks through Intrinsic Dimension

Despite their impressive performance in classification, neural networks are known to be vulnerable to adversarial attacks. These attacks are small perturbations of the input data designed to fool the model. Naturally, a question arises regarding the potential connection between the architecture, settings, or properties of the model and the nature of the attack. In this work, we aim to shed light on this problem by focusing on the implicit bias of the neural network, which refers to its inherent inclination to favor specific patterns or outcomes. Specifically, we investigate one aspect of the implicit bias, which involves the essential Fourier frequencies required for accurate image classification. We conduct tests to assess the statistical relationship between these frequencies and those necessary for a successful attack. To delve into this relationship, we propose a new method that can uncover non-linear correlations between sets of coordinates, which, in our case, are the aforementioned frequencies. By exploiting the entanglement between intrinsic dimension and correlation, we provide empirical evidence that the network bias in Fourier space and the target frequencies of adversarial attacks are closely tied.

Understanding robustness and generalization of artificial neural networks through Fourier masks

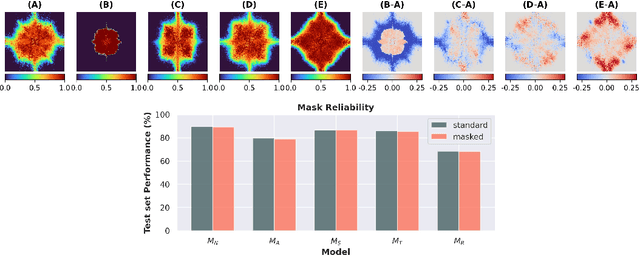
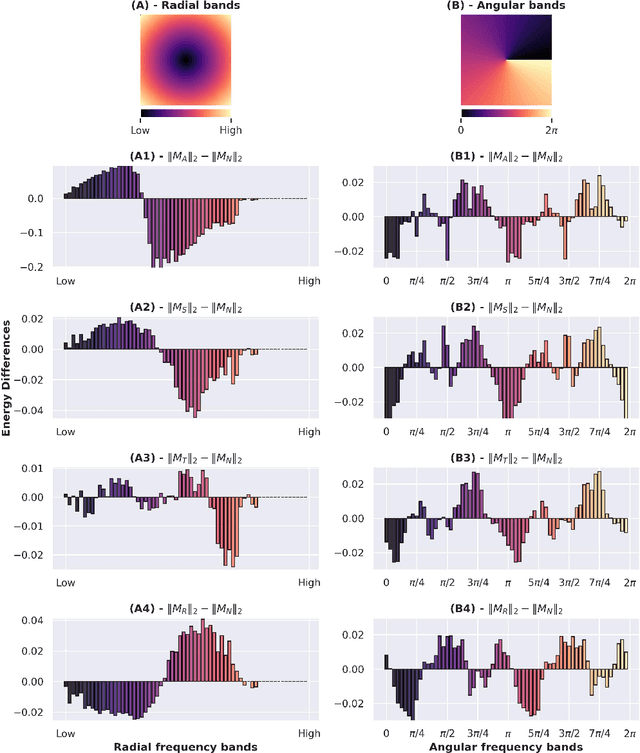
Despite the enormous success of artificial neural networks (ANNs) in many disciplines, the characterization of their computations and the origin of key properties such as generalization and robustness remain open questions. Recent literature suggests that robust networks with good generalization properties tend to be biased towards processing low frequencies in images. To explore the frequency bias hypothesis further, we develop an algorithm that allows us to learn modulatory masks highlighting the essential input frequencies needed for preserving a trained network's performance. We achieve this by imposing invariance in the loss with respect to such modulations in the input frequencies. We first use our method to test the low-frequency preference hypothesis of adversarially trained or data-augmented networks. Our results suggest that adversarially robust networks indeed exhibit a low-frequency bias but we find this bias is also dependent on directions in frequency space. However, this is not necessarily true for other types of data augmentation. Our results also indicate that the essential frequencies in question are effectively the ones used to achieve generalization in the first place. Surprisingly, images seen through these modulatory masks are not recognizable and resemble texture-like patterns.

A computational model for grid maps in neural populations

Grid cells in the entorhinal cortex, together with place, speed and border cells, are major contributors to the organization of spatial representations in the brain. In this contribution we introduce a novel theoretical and algorithmic framework able to explain the emergence of hexagonal grid-like response patterns from the statistics of the input stimuli. We show that this pattern is a result of minimal variance encoding of neurons. The novelty lies into the formulation of the encoding problem through the modern Frame Theory language, specifically that of equiangular Frames, providing new insights about the optimality of hexagonal grid receptive fields. The model proposed overcomes some crucial limitations of the current attractor and oscillatory models. It is based on the well-accepted and tested hypothesis of Hebbian learning, providing a simplified cortical-based framework that does not require the presence of theta velocity-driven oscillations (oscillatory model) or translational symmetries in the synaptic connections (attractor model). We moreover demonstrate that the proposed encoding mechanism naturally maps shifts, rotations and scaling of the stimuli onto the shape of grid cells' receptive fields, giving a straightforward explanation of the experimental evidence of grid cells remapping under transformations of environmental cues.

View-tolerant face recognition and Hebbian learning imply mirror-symmetric neural tuning to head orientation

The primate brain contains a hierarchy of visual areas, dubbed the ventral stream, which rapidly computes object representations that are both specific for object identity and relatively robust against identity-preserving transformations like depth-rotations. Current computational models of object recognition, including recent deep learning networks, generate these properties through a hierarchy of alternating selectivity-increasing filtering and tolerance-increasing pooling operations, similar to simple-complex cells operations. While simulations of these models recapitulate the ventral stream's progression from early view-specific to late view-tolerant representations, they fail to generate the most salient property of the intermediate representation for faces found in the brain: mirror-symmetric tuning of the neural population to head orientation. Here we prove that a class of hierarchical architectures and a broad set of biologically plausible learning rules can provide approximate invariance at the top level of the network. While most of the learning rules do not yield mirror-symmetry in the mid-level representations, we characterize a specific biologically-plausible Hebb-type learning rule that is guaranteed to generate mirror-symmetric tuning to faces tuning at intermediate levels of the architecture.

Deep Convolutional Networks are Hierarchical Kernel Machines

In i-theory a typical layer of a hierarchical architecture consists of HW modules pooling the dot products of the inputs to the layer with the transformations of a few templates under a group. Such layers include as special cases the convolutional layers of Deep Convolutional Networks (DCNs) as well as the non-convolutional layers (when the group contains only the identity). Rectifying nonlinearities -- which are used by present-day DCNs -- are one of the several nonlinearities admitted by i-theory for the HW module. We discuss here the equivalence between group averages of linear combinations of rectifying nonlinearities and an associated kernel. This property implies that present-day DCNs can be exactly equivalent to a hierarchy of kernel machines with pooling and non-pooling layers. Finally, we describe a conjecture for theoretically understanding hierarchies of such modules. A main consequence of the conjecture is that hierarchies of trained HW modules minimize memory requirements while computing a selective and invariant representation.

On Invariance and Selectivity in Representation Learning

We discuss data representation which can be learned automatically from data, are invariant to transformations, and at the same time selective, in the sense that two points have the same representation only if they are one the transformation of the other. The mathematical results here sharpen some of the key claims of i-theory -- a recent theory of feedforward processing in sensory cortex.

Unsupervised Learning of Invariant Representations in Hierarchical Architectures

The present phase of Machine Learning is characterized by supervised learning algorithms relying on large sets of labeled examples ($n \to \infty$). The next phase is likely to focus on algorithms capable of learning from very few labeled examples ($n \to 1$), like humans seem able to do. We propose an approach to this problem and describe the underlying theory, based on the unsupervised, automatic learning of a ``good'' representation for supervised learning, characterized by small sample complexity ($n$). We consider the case of visual object recognition though the theory applies to other domains. The starting point is the conjecture, proved in specific cases, that image representations which are invariant to translations, scaling and other transformations can considerably reduce the sample complexity of learning. We prove that an invariant and unique (discriminative) signature can be computed for each image patch, $I$, in terms of empirical distributions of the dot-products between $I$ and a set of templates stored during unsupervised learning. A module performing filtering and pooling, like the simple and complex cells described by Hubel and Wiesel, can compute such estimates. Hierarchical architectures consisting of this basic Hubel-Wiesel moduli inherit its properties of invariance, stability, and discriminability while capturing the compositional organization of the visual world in terms of wholes and parts. The theory extends existing deep learning convolutional architectures for image and speech recognition. It also suggests that the main computational goal of the ventral stream of visual cortex is to provide a hierarchical representation of new objects/images which is invariant to transformations, stable, and discriminative for recognition---and that this representation may be continuously learned in an unsupervised way during development and visual experience.