A Discrete Particle Swarm Optimizer for the Design of Cryptographic Boolean Functions

A Particle Swarm Optimizer for the search of balanced Boolean functions with good cryptographic properties is proposed in this paper. The algorithm is a modified version of the permutation PSO by Hu, Eberhart and Shi which preserves the Hamming weight of the particles positions, coupled with the Hill Climbing method devised by Millan, Clark and Dawson to improve the nonlinearity and deviation from correlation immunity of Boolean functions. The parameters for the PSO velocity equation are tuned by means of two meta-optimization techniques, namely Local Unimodal Sampling (LUS) and Continuous Genetic Algorithms (CGA), finding that CGA produces better results. Using the CGA-evolved parameters, the PSO algorithm is then run on the spaces of Boolean functions from $n=7$ to $n=12$ variables. The results of the experiments are reported, observing that this new PSO algorithm generates Boolean functions featuring similar or better combinations of nonlinearity, correlation immunity and propagation criterion with respect to the ones obtained by other optimization methods.

Local Search, Semantics, and Genetic Programming: a Global Analysis

Geometric Semantic Geometric Programming (GSGP) is one of the most prominent Genetic Programming (GP) variants, thanks to its solid theoretical background, the excellent performance achieved, and the execution time significantly smaller than standard syntax-based GP. In recent years, a new mutation operator, Geometric Semantic Mutation with Local Search (GSM-LS), has been proposed to include a local search step in the mutation process based on the idea that performing a linear regression during the mutation can allow for a faster convergence to good-quality solutions. While GSM-LS helps the convergence of the evolutionary search, it is prone to overfitting. Thus, it was suggested to use GSM-LS only for a limited number of generations and, subsequently, to switch back to standard geometric semantic mutation. A more recently defined variant of GSGP (called GSGP-reg) also includes a local search step but shares similar strengths and weaknesses with GSM-LS. Here we explore multiple possibilities to limit the overfitting of GSM-LS and GSGP-reg, ranging from adaptive methods to estimate the risk of overfitting at each mutation to a simple regularized regression. The results show that the method used to limit overfitting is not that important: providing that a technique to control overfitting is used, it is possible to consistently outperform standard GSGP on both training and unseen data. The obtained results allow practitioners to better understand the role of local search in GSGP and demonstrate that simple regularization strategies are effective in controlling overfitting.

Evolutionary Strategies for the Design of Binary Linear Codes

The design of binary error-correcting codes is a challenging optimization problem with several applications in telecommunications and storage, which has also been addressed with metaheuristic techniques and evolutionary algorithms. Still, all these efforts focused on optimizing the minimum distance of unrestricted binary codes, i.e., with no constraints on their linearity, which is a desirable property for efficient implementations. In this paper, we present an Evolutionary Strategy (ES) algorithm that explores only the subset of linear codes of a fixed length and dimension. To that end, we represent the candidate solutions as binary matrices and devise variation operators that preserve their ranks. Our experiments show that up to length $n=14$, our ES always converges to an optimal solution with a full success rate, and the evolved codes are all inequivalent to the Best-Known Linear Code (BKLC) given by MAGMA. On the other hand, for larger lengths, both the success rate of the ES as well as the diversity of the evolved codes start to drop, with the extreme case of $(16,8,5)$ codes which all turn out to be equivalent to MAGMA's BKLC.

The Influence of Local Search over Genetic Algorithms with Balanced Representations

We continue the study of Genetic Algorithms (GA) on combinatorial optimization problems where the candidate solutions need to satisfy a balancedness constraint. It has been observed that the reduction of the search space size granted by ad-hoc crossover and mutation operators does not usually translate to a substantial improvement of the GA performances. There is still no clear explanation of this phenomenon, although it is suspected that a balanced representation might yield a more irregular fitness landscape, where it could be more difficult for GA to converge to a global optimum. In this paper, we investigate this issue by adding a local search step to a GA with balanced operators, and use it to evolve highly nonlinear balanced Boolean functions. In particular, we organize our experiments around two research questions, namely if local search (1) improves the convergence speed of GA, and (2) decreases the population diversity. Surprisingly, while our results answer affirmatively the first question, they also show that adding local search actually \emph{increases} the diversity among the individuals in the population. We link these findings to some recent results on fitness landscape analysis for problems on Boolean functions.

The Effect of Multi-Generational Selection in Geometric Semantic Genetic Programming

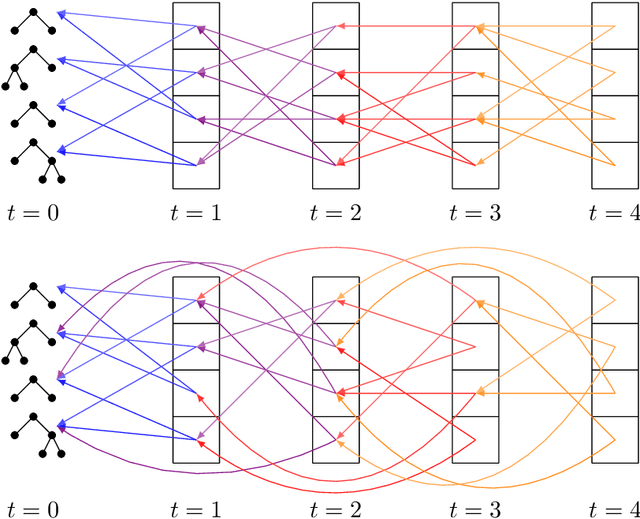
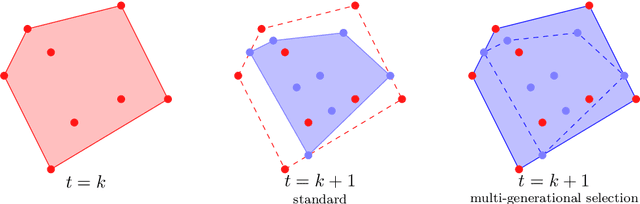
Among the evolutionary methods, one that is quite prominent is Genetic Programming, and, in recent years, a variant called Geometric Semantic Genetic Programming (GSGP) has shown to be successfully applicable to many real-world problems. Due to a peculiarity in its implementation, GSGP needs to store all the evolutionary history, i.e., all populations from the first one. We exploit this stored information to define a multi-generational selection scheme that is able to use individuals from older populations. We show that a limited ability to use "old" generations is actually useful for the search process, thus showing a zero-cost way of improving the performances of GSGP.

Salp Swarm Optimization: a Critical Review

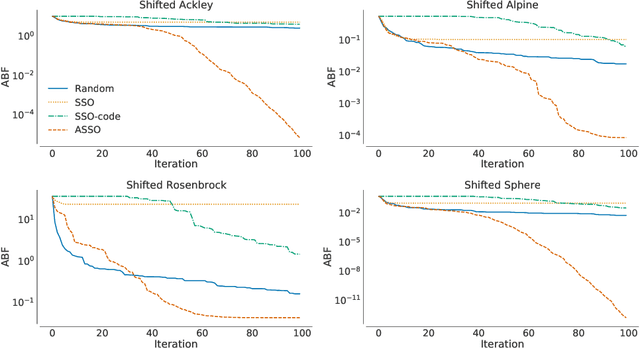
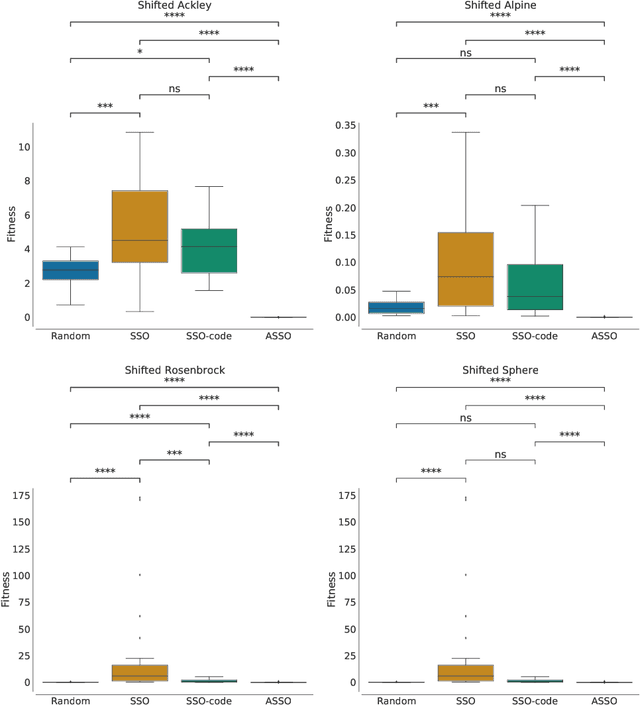
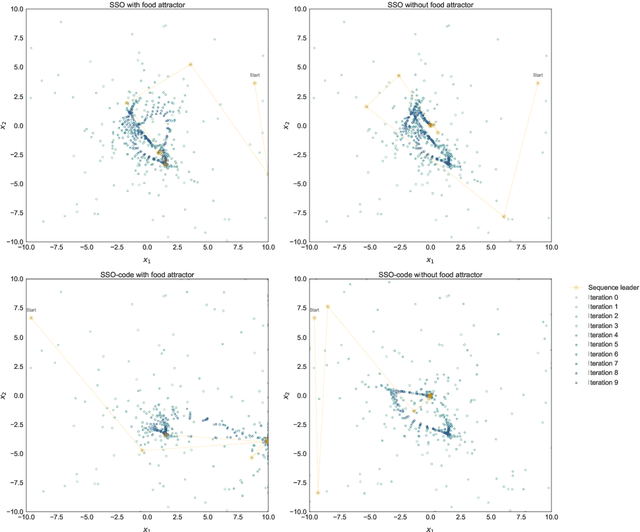
In the crowded environment of bio-inspired population-based meta-heuristics, the Salp Swarm Optimization (SSO) algorithm recently appeared and immediately gained a lot of momentum. Inspired by the peculiar spatial arrangement of salp colonies, which are displaced in long chains following a leader, this algorithm seems to provide interesting optimization performances. However, the original work was characterized by some conceptual and mathematical flaws, which influenced all ensuing papers on the subject. In this manuscript, we perform a critical review of SSO, highlighting all the issues present in the literature and their negative effects on the optimization process carried out by the algorithm. We also propose a mathematically correct version of SSO, named Amended Salp Swarm Optimizer (ASSO) that fixes all the discussed problems. Finally, we benchmark the performance of ASSO on a set of tailored experiments, showing it achieves better results than the original SSO.

Towards an evolutionary-based approach for natural language processing

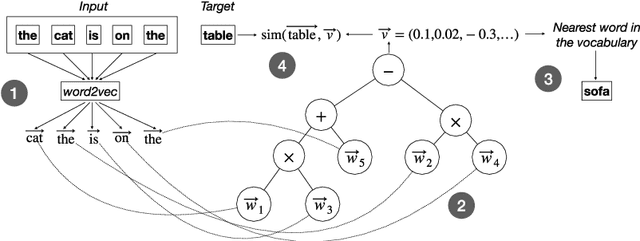
Tasks related to Natural Language Processing (NLP) have recently been the focus of a large research endeavor by the machine learning community. The increased interest in this area is mainly due to the success of deep learning methods. Genetic Programming (GP), however, was not under the spotlight with respect to NLP tasks. Here, we propose a first proof-of-concept that combines GP with the well established NLP tool word2vec for the next word prediction task. The main idea is that, once words have been moved into a vector space, traditional GP operators can successfully work on vectors, thus producing meaningful words as the output. To assess the suitability of this approach, we perform an experimental evaluation on a set of existing newspaper headlines. Individuals resulting from this (pre-)training phase can be employed as the initial population in other NLP tasks, like sentence generation, which will be the focus of future investigations, possibly employing adversarial co-evolutionary approaches.

Tip the Balance: Improving Exploration of Balanced Crossover Operators by Adaptive Bias

The use of balanced crossover operators in Genetic Algorithms (GA) ensures that the binary strings generated as offsprings have the same Hamming weight of the parents, a constraint which is sought in certain discrete optimization problems. Although this method reduces the size of the search space, the resulting fitness landscape often becomes more difficult for the GA to explore and to discover optimal solutions. This issue has been studied in this paper by applying an adaptive bias strategy to a counter-based crossover operator that introduces unbalancedness in the offspring with a certain probability, which is decreased throughout the evolutionary process. Experiments show that improving the exploration of the search space with this adaptive bias strategy is beneficial for the GA performances in terms of the number of optimal solutions found for the balanced nonlinear Boolean functions problem.

CoInGP: Convolutional Inpainting with Genetic Programming

We investigate the use of Genetic Programming (GP) as a convolutional predictor for supervised learning tasks in signal processing, focusing on the use case of predicting missing pixels in images. The training is performed by sweeping a small sliding window on the available pixels: all pixels in the window except for the central one are fed in input to a GP tree whose output is taken as the predicted value for the central pixel. The best GP tree in the population scoring the lowest prediction error over all available pixels in the population is then tested on the actual missing pixels of the degraded image. We experimentally assess this approach by training over four target images, removing up to 20\% of the pixels for the testing phase. The results indicate that our method can learn to some extent the distribution of missing pixels in an image and that GP with Moore neighborhood works better than the Von Neumann neighborhood, although the latter allows for a larger training set size.

Balanced Crossover Operators in Genetic Algorithms

In several combinatorial optimization problems arising in cryptography and design theory, the admissible solutions must often satisfy a balancedness constraint, such as being represented by bitstrings with a fixed number of ones. For this reason, several works in the literature tackling these optimization problems with Genetic Algorithms (GA) introduced new balanced crossover operators which ensure that the offspring has the same balancedness characteristics of the parents. However, the use of such operators has never been thoroughly motivated, except for some generic considerations about search space reduction. In this paper, we undertake a rigorous statistical investigation on the effect of balanced and unbalanced crossover operators against three optimization problems from the area of cryptography and coding theory: nonlinear balanced Boolean functions, binary Orthogonal Arrays (OA) and bent functions. In particular, we consider three different balanced crossover operators, two of which have never been published before, and compare their performances with classic one-point crossover. The statistical comparison shows that for the problems of nonlinear balanced Boolean functions and binary OA the use of balanced crossover operators gives GA a definite advantage over one-point crossover. For the case of bent functions, the situation is reversed, with the unbalanced crossover providing the best performances.