A Discrete Particle Swarm Optimizer for the Design of Cryptographic Boolean Functions

A Particle Swarm Optimizer for the search of balanced Boolean functions with good cryptographic properties is proposed in this paper. The algorithm is a modified version of the permutation PSO by Hu, Eberhart and Shi which preserves the Hamming weight of the particles positions, coupled with the Hill Climbing method devised by Millan, Clark and Dawson to improve the nonlinearity and deviation from correlation immunity of Boolean functions. The parameters for the PSO velocity equation are tuned by means of two meta-optimization techniques, namely Local Unimodal Sampling (LUS) and Continuous Genetic Algorithms (CGA), finding that CGA produces better results. Using the CGA-evolved parameters, the PSO algorithm is then run on the spaces of Boolean functions from $n=7$ to $n=12$ variables. The results of the experiments are reported, observing that this new PSO algorithm generates Boolean functions featuring similar or better combinations of nonlinearity, correlation immunity and propagation criterion with respect to the ones obtained by other optimization methods.

Evolutionary Construction of Perfectly Balanced Boolean Functions

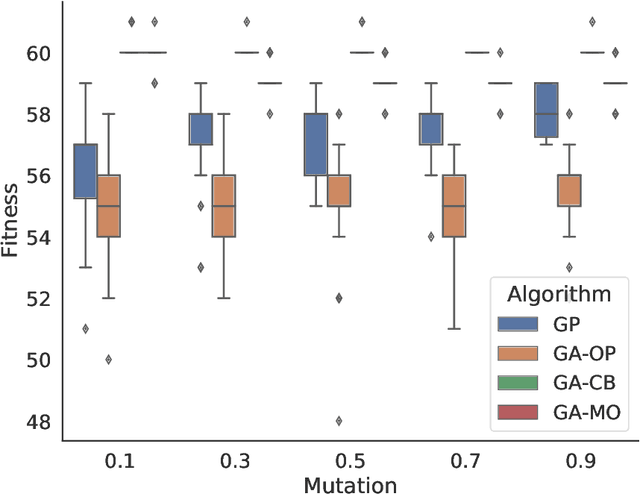
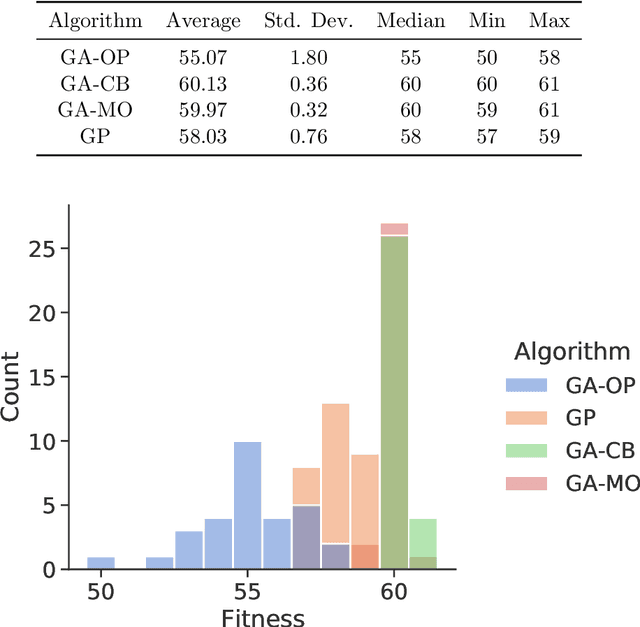
Finding Boolean functions suitable for cryptographic primitives is a complex combinatorial optimization problem, since they must satisfy several properties to resist cryptanalytic attacks, and the space is very large, which grows super exponentially with the number of input variables. Recent research has focused on the study of Boolean functions that satisfy properties on restricted sets of inputs due to their importance in the development of the FLIP stream cipher. In this paper, we consider one such property, perfect balancedness, and investigate the use of Genetic Programming (GP) and Genetic Algorithms (GA) to construct Boolean functions that satisfy this property along with a good nonlinearity profile. We formulate the related optimization problem and define two encodings for the candidate solutions, namely the truth table and the weightwise balanced representations. Somewhat surprisingly, the results show that GA with the weightwise balanced representation outperforms GP with the classical truth table phenotype in finding highly nonlinear WPB functions. This finding is in stark contrast to previous findings on the evolution of globally balanced Boolean functions, where GP always performs best.

On the Difficulty of Evolving Permutation Codes

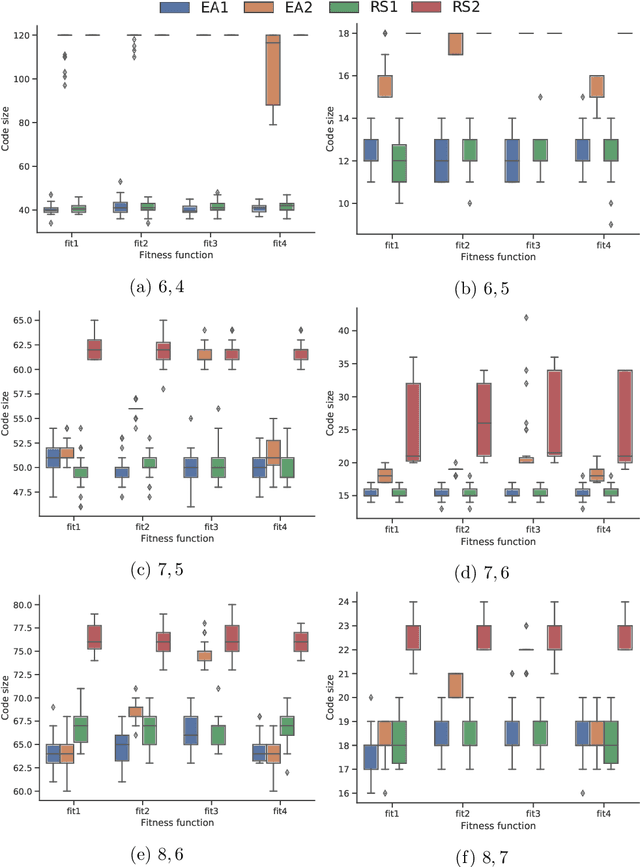
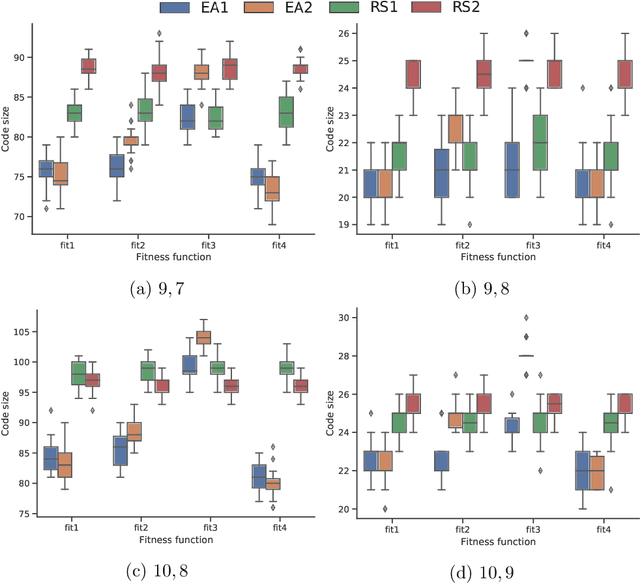
Combinatorial designs provide an interesting source of optimization problems. Among them, permutation codes are particularly interesting given their applications in powerline communications, flash memories, and block ciphers. This paper addresses the design of permutation codes by evolutionary algorithms (EA) by developing an iterative approach. Starting from a single random permutation, new permutations satisfying the minimum distance constraint are incrementally added to the code by using a permutation-based EA. We investigate our approach against four different fitness functions targeting the minimum distance requirement at different levels of detail and with two different policies concerning code expansion and pruning. We compare the results achieved by our EA approach to those of a simple random search, remarking that neither method scales well with the problem size.

Evolutionary Algorithms for Designing Reversible Cellular Automata

Reversible Cellular Automata (RCA) are a particular kind of shift-invariant transformations characterized by a dynamics composed only of disjoint cycles. They have many applications in the simulation of physical systems, cryptography and reversible computing. In this work, we formulate the search of a specific class of RCA -- namely, those whose local update rules are defined by conserved landscapes -- as an optimization problem to be tackled with Genetic Algorithms (GA) and Genetic Programming (GP). In particular, our experimental investigation revolves around three different research questions, which we address through a single-objective, a multi-objective, and a lexicographic approach. The results obtained from our experiments corroborate the previous findings and shed new light on 1) the difficulty of the associated optimization problem for GA and GP, 2) the relevance of conserved landscape CA in the domain of cryptography and reversible computing, and 3) the relationship between the reversibility property and the Hamming weight.