Gloria Pietropolli
Combining Genetic Programming and Particle Swarm Optimization to Simplify Rugged Landscapes Exploration
Jun 07, 2022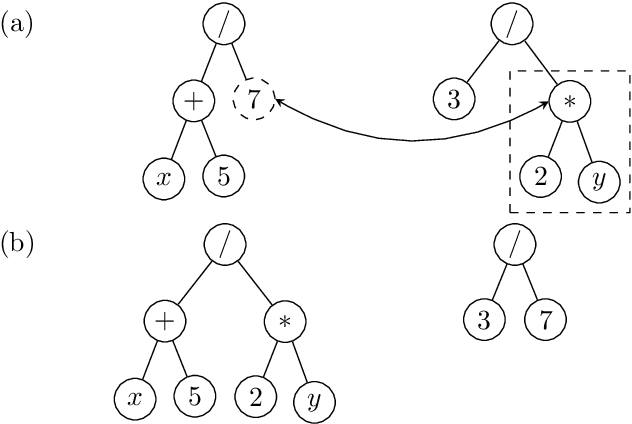
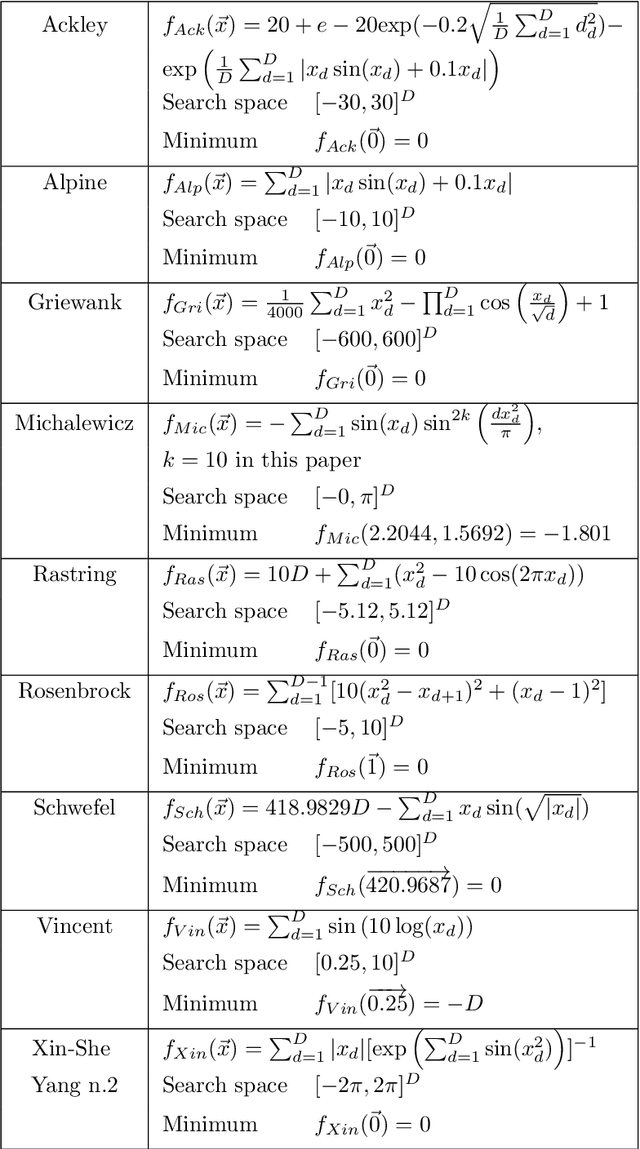

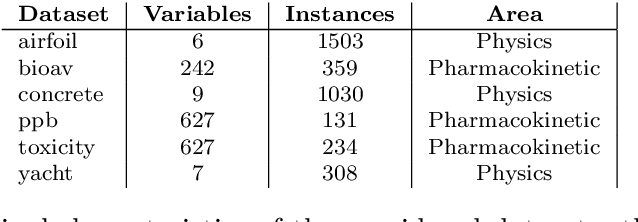
Abstract:Most real-world optimization problems are difficult to solve with traditional statistical techniques or with metaheuristics. The main difficulty is related to the existence of a considerable number of local optima, which may result in the premature convergence of the optimization process. To address this problem, we propose a novel heuristic method for constructing a smooth surrogate model of the original function. The surrogate function is easier to optimize but maintains a fundamental property of the original rugged fitness landscape: the location of the global optimum. To create such a surrogate model, we consider a linear genetic programming approach enhanced by a self-tuning fitness function. The proposed algorithm, called the GP-FST-PSO Surrogate Model, achieves satisfactory results in both the search for the global optimum and the production of a visual approximation of the original benchmark function (in the 2-dimensional case).
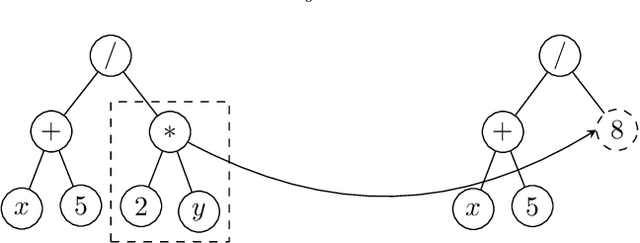
The Effect of Multi-Generational Selection in Geometric Semantic Genetic Programming
May 05, 2022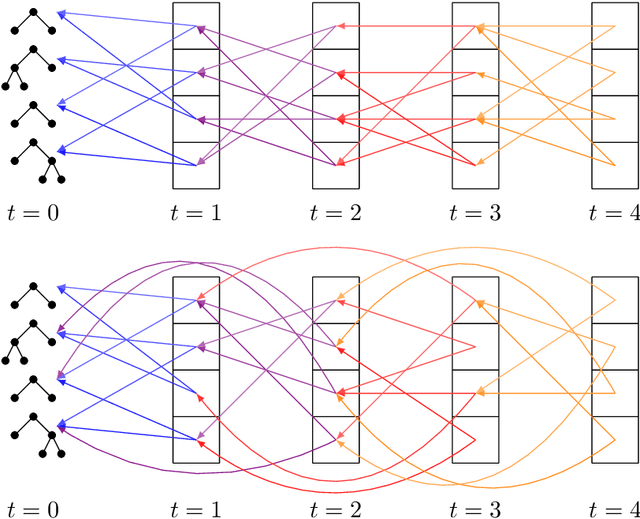
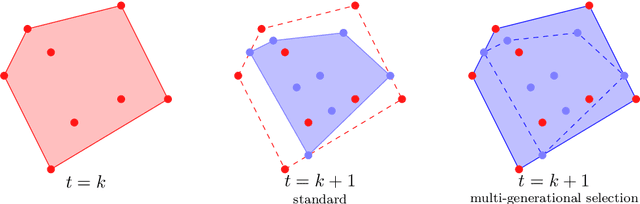

Abstract:Among the evolutionary methods, one that is quite prominent is Genetic Programming, and, in recent years, a variant called Geometric Semantic Genetic Programming (GSGP) has shown to be successfully applicable to many real-world problems. Due to a peculiarity in its implementation, GSGP needs to store all the evolutionary history, i.e., all populations from the first one. We exploit this stored information to define a multi-generational selection scheme that is able to use individuals from older populations. We show that a limited ability to use "old" generations is actually useful for the search process, thus showing a zero-cost way of improving the performances of GSGP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge