A Systematic Study on the Design of Odd-Sized Highly Nonlinear Boolean Functions via Evolutionary Algorithms

This paper focuses on the problem of evolving Boolean functions of odd sizes with high nonlinearity, a property of cryptographic relevance. Despite its simple formulation, this problem turns out to be remarkably difficult. We perform a systematic evaluation by considering three solution encodings and four problem instances, analyzing how well different types of evolutionary algorithms behave in finding a maximally nonlinear Boolean function. Our results show that genetic programming generally outperforms other evolutionary algorithms, although it falls short of the best-known results achieved by ad-hoc heuristics. Interestingly, by adding local search and restricting the space to rotation symmetric Boolean functions, we show that a genetic algorithm with the bitstring encoding manages to evolve a $9$-variable Boolean function with nonlinearity 241.

Degree is Important: On Evolving Homogeneous Boolean Functions

Boolean functions with good cryptographic properties like high nonlinearity and algebraic degree play an important in the security of stream and block ciphers. Such functions may be designed, for instance, by algebraic constructions or metaheuristics. This paper investigates the use of Evolutionary Algorithms (EAs) to design homogeneous bent Boolean functions, i.e., functions that are maximally nonlinear and whose algebraic normal form contains only monomials of the same degree. In our work, we evaluate three genotype encodings and four fitness functions. Our results show that while EAs manage to find quadratic homogeneous bent functions (with the best method being a GA leveraging a restricted encoding), none of the approaches result in cubic homogeneous bent functions.

The More the Merrier: On Evolving Five-valued Spectra Boolean Functions

Evolving Boolean functions with specific properties is an interesting optimization problem since, depending on the combination of properties and Boolean function size, the problem can range from very simple to (almost) impossible to solve. Moreover, some problems are more interesting as there may be only a few options for generating the required Boolean functions. This paper investigates one such problem: evolving five-valued spectra Boolean functions, which are the functions whose Walsh-Hadamard coefficients can only take five distinct values. We experimented with three solution encodings, two fitness functions, and 12 Boolean function sizes and showed that the tree encoding is superior to other choices, as we can obtain five-valued Boolean functions with high nonlinearity.

A Systematic Evaluation of Evolving Highly Nonlinear Boolean Functions in Odd Sizes

Boolean functions are mathematical objects used in diverse applications. Different applications also have different requirements, making the research on Boolean functions very active. In the last 30 years, evolutionary algorithms have been shown to be a strong option for evolving Boolean functions in different sizes and with different properties. Still, most of those works consider similar settings and provide results that are mostly interesting from the evolutionary algorithm's perspective. This work considers the problem of evolving highly nonlinear Boolean functions in odd sizes. While the problem formulation sounds simple, the problem is remarkably difficult, and the related work is extremely scarce. We consider three solutions encodings and four Boolean function sizes and run a detailed experimental analysis. Our results show that the problem is challenging, and finding optimal solutions is impossible except for the smallest tested size. However, once we added local search to the evolutionary algorithm, we managed to find a Boolean function in nine inputs with nonlinearity 241, which, to our knowledge, had never been accomplished before with evolutionary algorithms.

A New Angle: On Evolving Rotation Symmetric Boolean Functions

Rotation symmetric Boolean functions represent an interesting class of Boolean functions as they are relatively rare compared to general Boolean functions. At the same time, the functions in this class can have excellent properties, making them interesting for various practical applications. The usage of metaheuristics to construct rotation symmetric Boolean functions is a direction that has been explored for almost twenty years. Despite that, there are very few results considering evolutionary computation methods. This paper uses several evolutionary algorithms to evolve rotation symmetric Boolean functions with different properties. Despite using generic metaheuristics, we obtain results that are competitive with prior work relying on customized heuristics. Surprisingly, we find that bitstring and floating point encodings work better than the tree encoding. Moreover, evolving highly nonlinear general Boolean functions is easier than rotation symmetric ones.

Look into the Mirror: Evolving Self-Dual Bent Boolean Functions

Bent Boolean functions are important objects in cryptography and coding theory, and there are several general approaches for constructing such functions. Metaheuristics proved to be a strong choice as they can provide many bent functions, even when the size of the Boolean function is large (e.g., more than 20 inputs). While bent Boolean functions represent only a small part of all Boolean functions, there are several subclasses of bent functions providing specific properties and challenges. One of the most interesting subclasses comprises (anti-)self-dual bent Boolean functions. This paper provides a detailed experimentation with evolutionary algorithms with the goal of evolving (anti-)self-dual bent Boolean functions. We experiment with two encodings and two fitness functions to directly evolve self-dual bent Boolean functions. Our experiments consider Boolean functions with sizes of up to 16 inputs, and we successfully construct self-dual bent functions for each dimension. Moreover, when comparing with the evolution of bent Boolean functions, we notice that the difficulty for evolutionary algorithms is rather similar. Finally, we also tried evolving secondary constructions for self-dual bent functions, but this direction provided no successful results.

Evolutionary Strategies for the Design of Binary Linear Codes

The design of binary error-correcting codes is a challenging optimization problem with several applications in telecommunications and storage, which has also been addressed with metaheuristic techniques and evolutionary algorithms. Still, all these efforts focused on optimizing the minimum distance of unrestricted binary codes, i.e., with no constraints on their linearity, which is a desirable property for efficient implementations. In this paper, we present an Evolutionary Strategy (ES) algorithm that explores only the subset of linear codes of a fixed length and dimension. To that end, we represent the candidate solutions as binary matrices and devise variation operators that preserve their ranks. Our experiments show that up to length $n=14$, our ES always converges to an optimal solution with a full success rate, and the evolved codes are all inequivalent to the Best-Known Linear Code (BKLC) given by MAGMA. On the other hand, for larger lengths, both the success rate of the ES as well as the diversity of the evolved codes start to drop, with the extreme case of $(16,8,5)$ codes which all turn out to be equivalent to MAGMA's BKLC.

Evolving Constructions for Balanced, Highly Nonlinear Boolean Functions

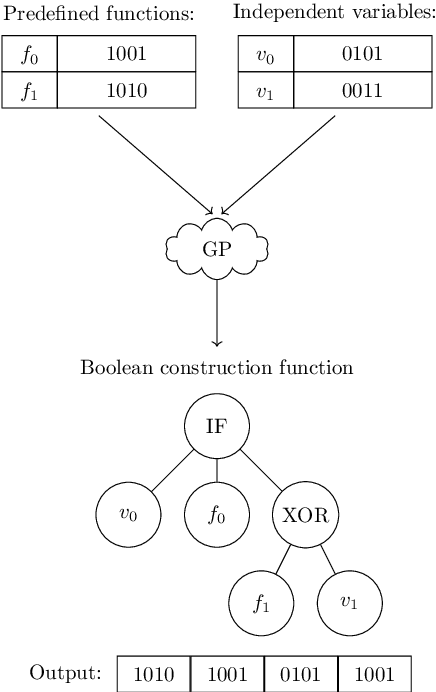
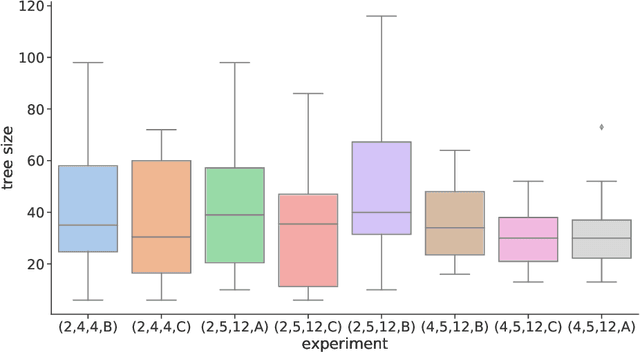
Finding balanced, highly nonlinear Boolean functions is a difficult problem where it is not known what nonlinearity values are possible to be reached in general. At the same time, evolutionary computation is successfully used to evolve specific Boolean function instances, but the approach cannot easily scale for larger Boolean function sizes. Indeed, while evolving smaller Boolean functions is almost trivial, larger sizes become increasingly difficult, and evolutionary algorithms perform suboptimally. In this work, we ask whether genetic programming (GP) can evolve constructions resulting in balanced Boolean functions with high nonlinearity. This question is especially interesting as there are only a few known such constructions. Our results show that GP can find constructions that generalize well, i.e., result in the required functions for multiple tested sizes. Further, we show that GP evolves many equivalent constructions under different syntactic representations. Interestingly, the simplest solution found by GP is a particular case of the well-known indirect sum construction.