Jim Mutch
Computational role of eccentricity dependent cortical magnification
Jun 06, 2014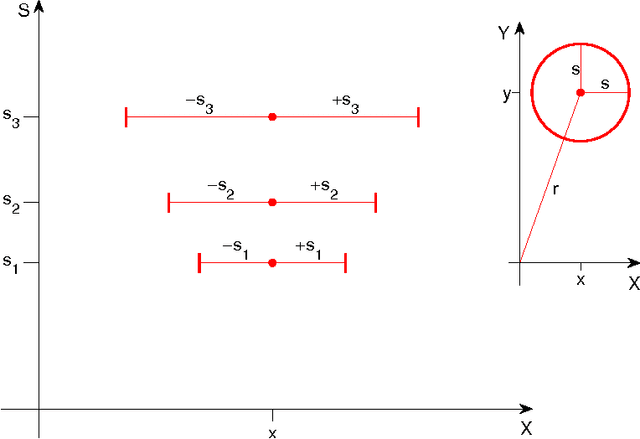
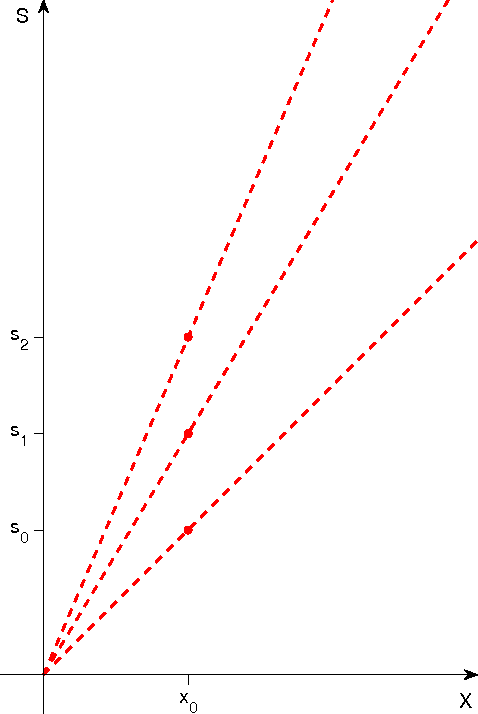
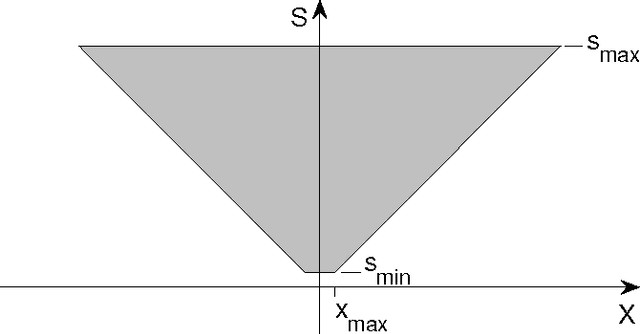
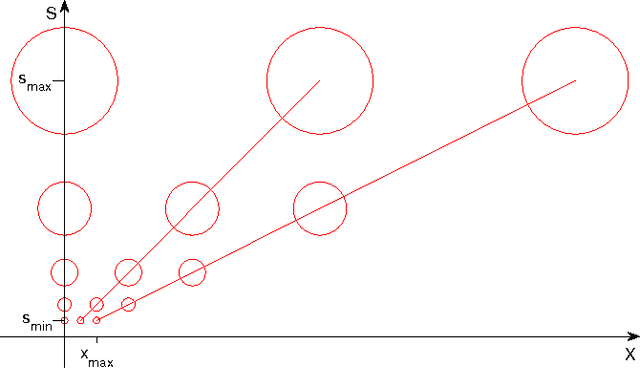
Abstract:We develop a sampling extension of M-theory focused on invariance to scale and translation. Quite surprisingly, the theory predicts an architecture of early vision with increasing receptive field sizes and a high resolution fovea -- in agreement with data about the cortical magnification factor, V1 and the retina. From the slope of the inverse of the magnification factor, M-theory predicts a cortical "fovea" in V1 in the order of $40$ by $40$ basic units at each receptive field size -- corresponding to a foveola of size around $26$ minutes of arc at the highest resolution, $\approx 6$ degrees at the lowest resolution. It also predicts uniform scale invariance over a fixed range of scales independently of eccentricity, while translation invariance should depend linearly on spatial frequency. Bouma's law of crowding follows in the theory as an effect of cortical area-by-cortical area pooling; the Bouma constant is the value expected if the signature responsible for recognition in the crowding experiments originates in V2. From a broader perspective, the emerging picture suggests that visual recognition under natural conditions takes place by composing information from a set of fixations, with each fixation providing recognition from a space-scale image fragment -- that is an image patch represented at a set of increasing sizes and decreasing resolutions.
Unsupervised Learning of Invariant Representations in Hierarchical Architectures
Mar 11, 2014



Abstract:The present phase of Machine Learning is characterized by supervised learning algorithms relying on large sets of labeled examples ($n \to \infty$). The next phase is likely to focus on algorithms capable of learning from very few labeled examples ($n \to 1$), like humans seem able to do. We propose an approach to this problem and describe the underlying theory, based on the unsupervised, automatic learning of a ``good'' representation for supervised learning, characterized by small sample complexity ($n$). We consider the case of visual object recognition though the theory applies to other domains. The starting point is the conjecture, proved in specific cases, that image representations which are invariant to translations, scaling and other transformations can considerably reduce the sample complexity of learning. We prove that an invariant and unique (discriminative) signature can be computed for each image patch, $I$, in terms of empirical distributions of the dot-products between $I$ and a set of templates stored during unsupervised learning. A module performing filtering and pooling, like the simple and complex cells described by Hubel and Wiesel, can compute such estimates. Hierarchical architectures consisting of this basic Hubel-Wiesel moduli inherit its properties of invariance, stability, and discriminability while capturing the compositional organization of the visual world in terms of wholes and parts. The theory extends existing deep learning convolutional architectures for image and speech recognition. It also suggests that the main computational goal of the ventral stream of visual cortex is to provide a hierarchical representation of new objects/images which is invariant to transformations, stable, and discriminative for recognition---and that this representation may be continuously learned in an unsupervised way during development and visual experience.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge